PEE Moduł 1: Różnice pomiędzy wersjami
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 15: | Linia 15: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M1_Slajd3.png]] | |valign="top" width="500px"|[[Grafika:PEE_M1_Slajd3.png]] | ||
|valign="top"| | |valign="top"|Teoria obwodów stanowi jedną z dziedzin elektrotechniki zajmującą się stroną teoretyczną zjawisk występujących w obwodach elektrycznych, w tym metodami analizy rozpływu prądów i rozkładu napięć obwodu w stanie ustalonym i nieustalonym. Przyjmuje się, że nośnikami elektryczności są cząstki elementarne: elektrony i protony występujące w atomie. W przypadku przewodników elektrycznych najważniejszą rolę odgrywają elektrony swobodne, stanowiące trwałe nośniki ujemnego ładunku <math>q</math>, wyzwolone z przyciągania jądra atomu oraz jony, stanowiące cząsteczki naładowane dodatnio lub ujemnie. Ładunek elektryczny elektronu, oznaczany jest literą <math>e\,</math> a jego wartość <math>e=1,602 \cdot 10^{-19}C</math>. | ||
Teoria obwodów stanowi jedną z dziedzin elektrotechniki zajmującą się stroną teoretyczną zjawisk występujących w obwodach elektrycznych, w tym metodami analizy rozpływu prądów i rozkładu napięć obwodu w stanie ustalonym i nieustalonym. Przyjmuje się, że nośnikami elektryczności są cząstki elementarne: elektrony i protony występujące w atomie. W przypadku przewodników elektrycznych najważniejszą rolę odgrywają elektrony swobodne, stanowiące trwałe nośniki ujemnego ładunku <math>q</math>, wyzwolone z przyciągania jądra atomu oraz jony, stanowiące cząsteczki naładowane dodatnio lub ujemnie. Ładunek elektryczny elektronu, oznaczany jest literą <math>e\,</math> a jego wartość <math>e=1,602 \cdot 10^{-19}C</math>. | |||
'''Prąd elektryczny''' powstaje jako uporządkowany ruch ładunków elektrycznych i jest utożsamiany w teorii obwodów z pojęciem natężenia prądu elektrycznego. W ogólności definiowany jest jako granica stosunku ładunku elektrycznego przepływającego przez przekrój poprzeczny elementu do rozpatrywanego czasu, gdy czas ten dąży do zera. Prąd elektryczny oznaczany będzie literą <math>i\,</math> (dużą lub małą). Jest wielkością skalarną a jej jednostką w układzie SI jest '''amper''' (<math>A\,</math>). Prąd mierzymy przyrządem zwanym amperomierzem, włączanym szeregowo do gałęzi, której prąd chcemy zmierzyć. Przyjmuje się, że amperomierz ma impedancję wewnętrzną równą zeru, a więc nie wpływa na rozpływy prądów w obwodzie. | '''Prąd elektryczny''' powstaje jako uporządkowany ruch ładunków elektrycznych i jest utożsamiany w teorii obwodów z pojęciem natężenia prądu elektrycznego. W ogólności definiowany jest jako granica stosunku ładunku elektrycznego przepływającego przez przekrój poprzeczny elementu do rozpatrywanego czasu, gdy czas ten dąży do zera. Prąd elektryczny oznaczany będzie literą <math>i\,</math> (dużą lub małą). Jest wielkością skalarną a jej jednostką w układzie SI jest '''amper''' (<math>A\,</math>). Prąd mierzymy przyrządem zwanym amperomierzem, włączanym szeregowo do gałęzi, której prąd chcemy zmierzyć. Przyjmuje się, że amperomierz ma impedancję wewnętrzną równą zeru, a więc nie wpływa na rozpływy prądów w obwodzie. | ||
| Linia 30: | Linia 28: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M1_Slajd4.png]] | |valign="top" width="500px"|[[Grafika:PEE_M1_Slajd4.png]] | ||
|valign="top"|Na strukturę obwodu elektrycznego poza elementami składają się również gałęzie, węzły i oczka. '''Gałąź''' obwodu jest tworzona przez jeden lub kilka elementów połączonych ze sobą w określony sposób. '''Węzłem''' obwodu jest zacisk będący końcówką gałęzi, do którego można dołączyć następną gałąź lub kilka gałęzi. Gałąź obwodu tworzą elementy ograniczone dwoma węzłami. '''Oczko''' obwodu to zbiór gałęzi połączonych ze sobą i tworzących drogę zamkniętą dla prądu elektrycznego. Oczko ma tę właściwość, że po usunięciu dowolnej gałęzi ze zbioru pozostałe gałęzie nie tworzą drogi zamkniętej. W obwodzie o zadanej strukturze istnieje ściśle określona liczba węzłów, natomiast liczba oczek jest wprawdzie skończona ale bliżej nieokreślona. | |valign="top"|Na strukturę obwodu elektrycznego poza elementami składają się również gałęzie, węzły i oczka. | ||
'''Gałąź''' obwodu jest tworzona przez jeden lub kilka elementów połączonych ze sobą w określony sposób. | |||
'''Węzłem''' obwodu jest zacisk będący końcówką gałęzi, do którego można dołączyć następną gałąź lub kilka gałęzi. Gałąź obwodu tworzą elementy ograniczone dwoma węzłami. | |||
'''Oczko''' obwodu to zbiór gałęzi połączonych ze sobą i tworzących drogę zamkniętą dla prądu elektrycznego. Oczko ma tę właściwość, że po usunięciu dowolnej gałęzi ze zbioru pozostałe gałęzie nie tworzą drogi zamkniętej. W obwodzie o zadanej strukturze istnieje ściśle określona liczba węzłów, natomiast liczba oczek jest wprawdzie skończona ale bliżej nieokreślona. | |||
|} | |} | ||
| Linia 56: | Linia 63: | ||
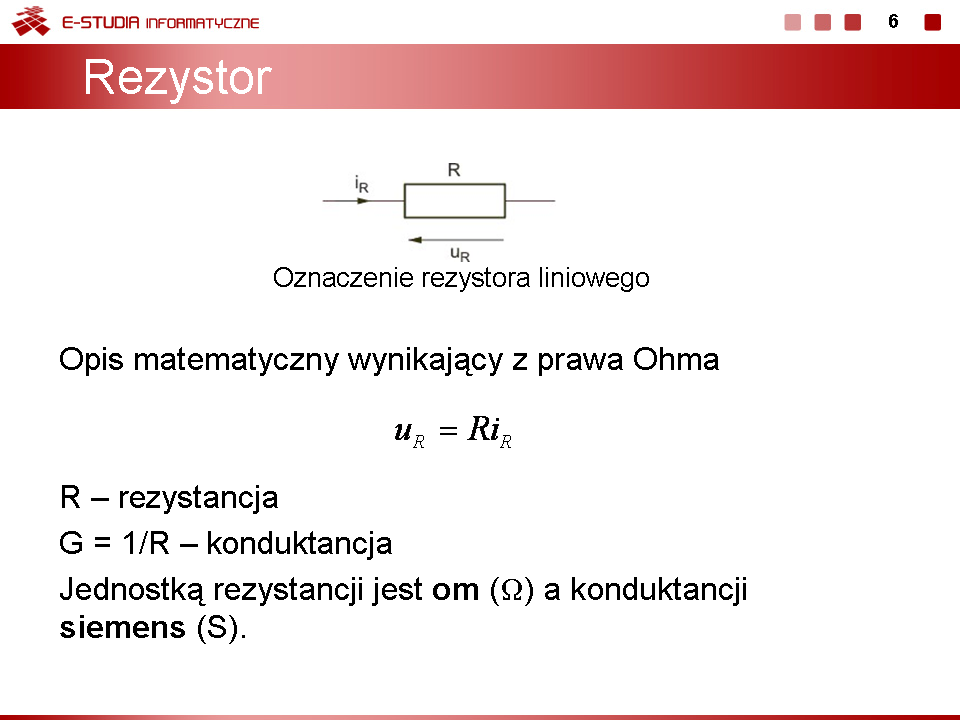
Opis matematyczny rezystora wynika z prawa Ohma, zgodnie z którym | Opis matematyczny rezystora wynika z prawa Ohma, zgodnie z którym | ||
: <math>u_R=R_{i_R}</math> | |||
<math>u_R=R_{i_R}</math> | |||
Wartość rezystancji rezystora liniowego przyjmuje określoną wartość (często stałą). Jednostką rezystancji jest '''om''' (<math>\Omega</math>) a konduktancji '''siemens''' (<math>S</math>). | Wartość rezystancji rezystora liniowego przyjmuje określoną wartość (często stałą). Jednostką rezystancji jest '''om''' (<math>\Omega</math>) a konduktancji '''siemens''' (<math>S</math>). | ||
| Linia 73: | Linia 78: | ||
Cewka zwana również induktorem należy również do klasy elementów pasywnych. Ma zdolność gromadzenia energii w polu magnetycznym. Cewce idealnej przypisuje się tylko jedną właściwość, zwaną '''indukcyjnością''' własną (w skrócie indukcyjnością) <math>L\,</math>. W przypadku cewki liniowej indukcyjność definiuje się jako stosunek strumienia <math>\Psi</math> skojarzonego z cewką do prądu płynącego przez nią, to znaczy | Cewka zwana również induktorem należy również do klasy elementów pasywnych. Ma zdolność gromadzenia energii w polu magnetycznym. Cewce idealnej przypisuje się tylko jedną właściwość, zwaną '''indukcyjnością''' własną (w skrócie indukcyjnością) <math>L\,</math>. W przypadku cewki liniowej indukcyjność definiuje się jako stosunek strumienia <math>\Psi</math> skojarzonego z cewką do prądu płynącego przez nią, to znaczy | ||
: <math>L={\Psi \over i_L}</math> | |||
<math>L={\Psi \over i_L}</math> | |||
Strumień skojarzony <math>\Psi</math> cewki o z zwojach jest równy sumie strumieni wszystkich zwojów cewki, to jest <math>\Psi = z\phi</math> (<math>\phi\,</math> - strumień skojarzony z jednym zwojem cewki, <math>z\,</math> – liczba zwojów). Jednostką indukcyjności jest '''henr''' (<math>H\,</math>), przy czym <math>1H = 1\Omega s</math>. Napięcie cewki wyrażone jest jako pochodna strumienia względem czasu | Strumień skojarzony <math>\Psi</math> cewki o z zwojach jest równy sumie strumieni wszystkich zwojów cewki, to jest <math>\Psi = z\phi</math> (<math>\phi\,</math> - strumień skojarzony z jednym zwojem cewki, <math>z\,</math> – liczba zwojów). Jednostką indukcyjności jest '''henr''' (<math>H\,</math>), przy czym <math>1H = 1\Omega s</math>. Napięcie cewki wyrażone jest jako pochodna strumienia względem czasu | ||
: <math>u_L={d\Psi \over dt}</math> | |||
<math>u_L={d\Psi \over dt}</math> | |||
W przypadku cewki liniowej o indukcyjności <math>L\,</math> niezależnej od czasu, dla której strumień jest iloczynem prądu <math>i\,</math> indukcyjności <math>L\,</math>, <math>\Psi=Li_L</math>, relacja napięciowo-prądowa upraszcza się do postaci | W przypadku cewki liniowej o indukcyjności <math>L\,</math> niezależnej od czasu, dla której strumień jest iloczynem prądu <math>i\,</math> indukcyjności <math>L\,</math>, <math>\Psi=Li_L</math>, relacja napięciowo-prądowa upraszcza się do postaci | ||
: <math>u_L=L{di_L \over dt}</math> | |||
<math>u_L=L{di_L \over dt}</math> | |||
Zauważmy, że przy stałej wartości prądu cewki i stałej wartości indukcyjności <math>L\,</math> napięcie na niej jest równe zeru, gdyż pochodna wartości stałej względem czasu jest równa zeru. Stąd cewka w stanie ustalonym obwodu przy prądzie stałym zachowuje się jak zwarcie (napięcie między końcówkami elementu równe zeru). | Zauważmy, że przy stałej wartości prądu cewki i stałej wartości indukcyjności <math>L\,</math> napięcie na niej jest równe zeru, gdyż pochodna wartości stałej względem czasu jest równa zeru. Stąd cewka w stanie ustalonym obwodu przy prądzie stałym zachowuje się jak zwarcie (napięcie między końcówkami elementu równe zeru). | ||
| Linia 100: | Linia 99: | ||
Kondensator jest elementem pasywnym, w którym istnieje możliwość gromadzenia energii w polu elektrycznym. Kondensatorowi idealnemu przypisuje się tylko jedną właściwość zwaną '''pojemnością''' <math>C\,</math>. W przypadku kondensatora liniowego pojemność <math>C\,</math> jest definiowana jako stosunek ładunku <math>q\,</math> zgromadzonego w kondensatorze do napięcia między okładzinami tego kondensatora | Kondensator jest elementem pasywnym, w którym istnieje możliwość gromadzenia energii w polu elektrycznym. Kondensatorowi idealnemu przypisuje się tylko jedną właściwość zwaną '''pojemnością''' <math>C\,</math>. W przypadku kondensatora liniowego pojemność <math>C\,</math> jest definiowana jako stosunek ładunku <math>q\,</math> zgromadzonego w kondensatorze do napięcia między okładzinami tego kondensatora | ||
: <math>C={q \over u_C}</math> | |||
<math>C={q \over u_C}</math> | |||
W układzie SI jednostką ładunku jest '''kulomb''' (<math>C\,</math>), a pojemności '''farad''' (<math>F\,</math>), przy czym <math>1 F = 1 C/V</math>. Zależność wiążąca napięcie i prąd kondensatora dana jest w postaci równania różniczkowego | W układzie SI jednostką ładunku jest '''kulomb''' (<math>C\,</math>), a pojemności '''farad''' (<math>F\,</math>), przy czym <math>1 F = 1 C/V</math>. Zależność wiążąca napięcie i prąd kondensatora dana jest w postaci równania różniczkowego | ||
<math>i_C={dq \over dt}=C{du_C \over dt}</math> | : <math>i_C={dq \over dt}=C{du_C \over dt}</math> | ||
Podobnie jak w przypadku cewki, jeśli napięcie na zaciskach kondensatora jest stałe, jego prąd jest równy zeru (pochodna wartości stałej względem czasu jest zerem). Kondensator zachowuje się wtedy jak przerwa (pomimo istnienia napięcia prąd nie płynie). | Podobnie jak w przypadku cewki, jeśli napięcie na zaciskach kondensatora jest stałe, jego prąd jest równy zeru (pochodna wartości stałej względem czasu jest zerem). Kondensator zachowuje się wtedy jak przerwa (pomimo istnienia napięcia prąd nie płynie). | ||
| Linia 184: | Linia 181: | ||
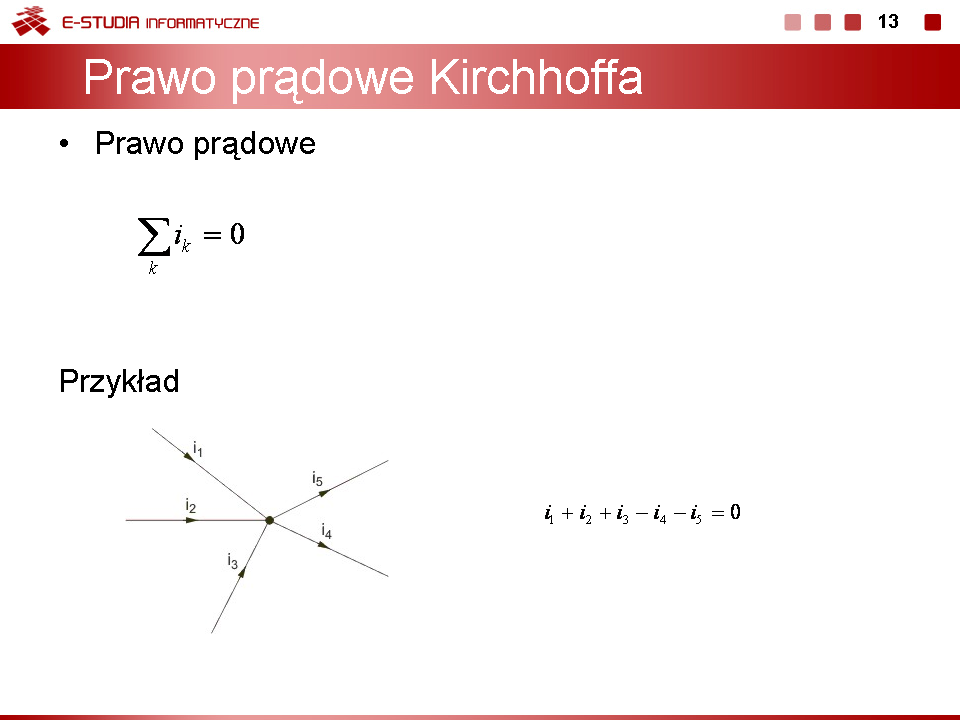
Suma prądów w każdym węźle obwodu elektrycznego jest równa zeru | Suma prądów w każdym węźle obwodu elektrycznego jest równa zeru | ||
<math>\sum_{k}=i_k=0\,</math> | : <math>\sum_{k}=i_k=0\,</math> | ||
Sumowanie dotyczy wszystkich prądów, które dopływają lub odpływają z danego oczka, przy czym wszystkie prądy wpływające do węzła brane są z jednakowym znakiem a wszystkie prądy wypływające z węzła ze znakiem przeciwnym (nie jest istotne czy znak plus dotyczy prądów wpływających czy wypływających). Sposób tworzenia równania prądowego Kirchhoffa zilustrujemy dla jednego węzła obwodu przedstawionego na rysunku obok. | Sumowanie dotyczy wszystkich prądów, które dopływają lub odpływają z danego oczka, przy czym wszystkie prądy wpływające do węzła brane są z jednakowym znakiem a wszystkie prądy wypływające z węzła ze znakiem przeciwnym (nie jest istotne czy znak plus dotyczy prądów wpływających czy wypływających). Sposób tworzenia równania prądowego Kirchhoffa zilustrujemy dla jednego węzła obwodu przedstawionego na rysunku obok. | ||
| Linia 190: | Linia 187: | ||
Prawo Kirchhoffa dla tego węzła z uwzględnieniem kierunków prądów w węźle zapiszemy w postaci: | Prawo Kirchhoffa dla tego węzła z uwzględnieniem kierunków prądów w węźle zapiszemy w postaci: | ||
<math>i_1+i_2+i_3-i_4-i_5=0</math> | : <math>i_1+i_2+i_3-i_4-i_5=0</math> | ||
Można je również zapisać jako bilans prądów dopływających i odpływających od węzła w postaci: | Można je również zapisać jako bilans prądów dopływających i odpływających od węzła w postaci: | ||
<math>i_1+i_2+i_3=i_4+i_5</math> | : <math>i_1+i_2+i_3=i_4+i_5</math> | ||
Dla każdego obwodu można napisać dokładnie <math>n-1\,</math> niezależnych równań prądowych, gdzie <math>n\,</math> oznacza całkowitą liczbę węzłów a <math>(n-1)</math> liczbę węzłów niezależnych. Bilans prądów w pozostałym <math>n\,</math>-tym węźle obwodu wynika z równań prądowych napisanych dla <math>n-1\,</math> węzłów (jest to węzeł zależny zwany węzłem odniesienia). Wybór węzła odniesienia jest całkowicie dowolny. | Dla każdego obwodu można napisać dokładnie <math>n-1\,</math> niezależnych równań prądowych, gdzie <math>n\,</math> oznacza całkowitą liczbę węzłów a <math>(n-1)</math> liczbę węzłów niezależnych. Bilans prądów w pozostałym <math>n\,</math>-tym węźle obwodu wynika z równań prądowych napisanych dla <math>n-1\,</math> węzłów (jest to węzeł zależny zwany węzłem odniesienia). Wybór węzła odniesienia jest całkowicie dowolny. | ||
| Linia 207: | Linia 204: | ||
Suma napięć w każdym oczku obwodu elektrycznego jest równa zeru | Suma napięć w każdym oczku obwodu elektrycznego jest równa zeru | ||
<math>\sum_k=u_k=0</math> | : <math>\sum_k=u_k=0</math> | ||
Sumowanie dotyczy napięć gałęziowych występujących w danym oczku zorientowanych względem dowolnie przyjętego kierunku odniesienia. Napięcie gałęziowe zgodne z tym kierunkiem jest brane z plusem a przeciwne z minusem. Sposób pisania równań wynikających z prawa napięciowego Kirchhoffa pokażemy na przykładzie oczka obwodu przedstawionego na rysunku obok. | Sumowanie dotyczy napięć gałęziowych występujących w danym oczku zorientowanych względem dowolnie przyjętego kierunku odniesienia. Napięcie gałęziowe zgodne z tym kierunkiem jest brane z plusem a przeciwne z minusem. Sposób pisania równań wynikających z prawa napięciowego Kirchhoffa pokażemy na przykładzie oczka obwodu przedstawionego na rysunku obok. | ||
| Linia 213: | Linia 210: | ||
Uwzględniając kierunki napięć gałęziowych równanie napięciowe Kirchhoffa dla tego oczka przyjmie postać: | Uwzględniając kierunki napięć gałęziowych równanie napięciowe Kirchhoffa dla tego oczka przyjmie postać: | ||
<math>u_1+u_2+u_3-u_4-e=0</math> | : <math>u_1+u_2+u_3-u_4-e=0</math> | ||
Można je również zapisać jako bilans napięć źródłowych i odbiornikowych w postaci: | Można je również zapisać jako bilans napięć źródłowych i odbiornikowych w postaci: | ||
<math>e=u_1+u_2+u_3-u_4</math> | : <math>e=u_1+u_2+u_3-u_4</math> | ||
Dla każdego obwodu można napisać tyle równań oczkowych ile oczek wyodrębnimy w tym obwodzie, przy czym część równań oczkowych będzie równaniami zależnymi (wynikającymi z liniowej kombinacji innych równań). Liczba równań oczkowych branych pod uwagę w analizie jest więc równa liczbie oczek niezależnych. | Dla każdego obwodu można napisać tyle równań oczkowych ile oczek wyodrębnimy w tym obwodzie, przy czym część równań oczkowych będzie równaniami zależnymi (wynikającymi z liniowej kombinacji innych równań). Liczba równań oczkowych branych pod uwagę w analizie jest więc równa liczbie oczek niezależnych. | ||
Wersja z 07:52, 30 sie 2006

|

|
Wykład 1 Podstawowe prawa obwodów elektrycznych |
| Zadania sprawdzające
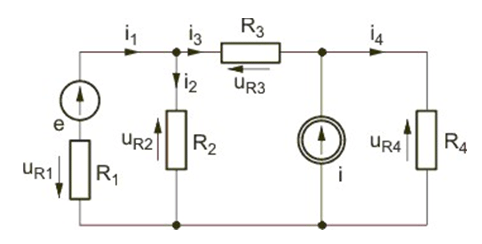
Stosując prawa Kirchhoffa wyznaczyć prądy w obwodzie przedstawionym na rysunku poniżej, jeśli , , , , a wartości źródeł są następujące: , . Rozwiązanie Korzystając z praw Kirchhoffa otrzymuje się układ równań opisujących obwód w postaci Po wstawieniu wartości liczbowych parametrów i rozwiązaniu układu równań otrzymuje się: , , oraz .
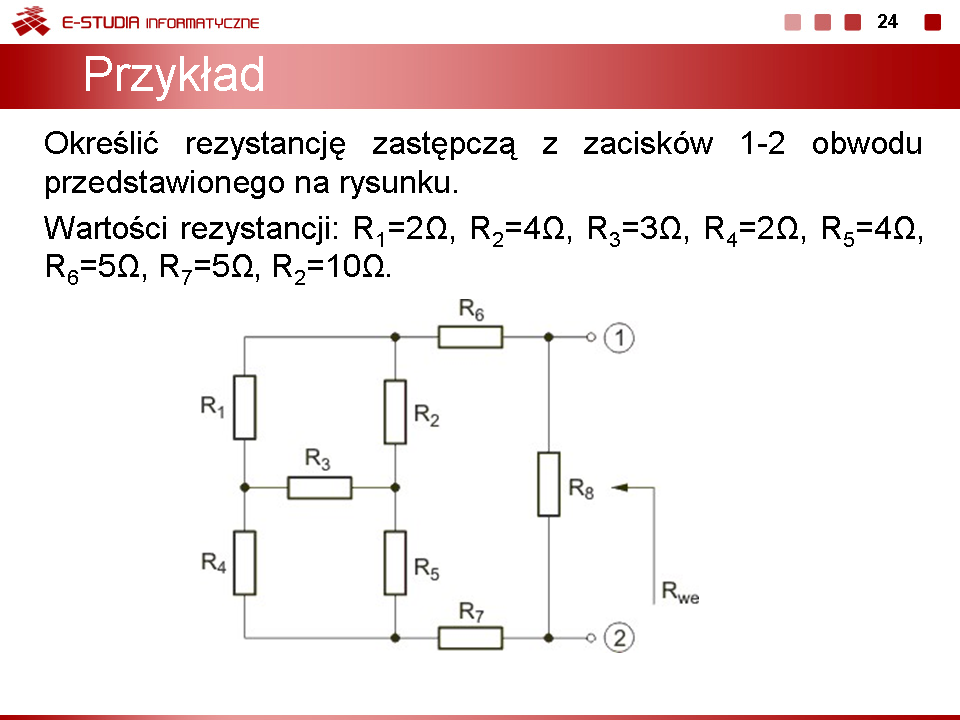
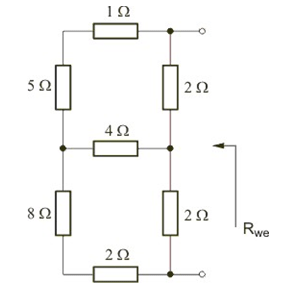
Wyznaczyć rezystancję wypadkową obwodu przedstawionego na rysunku poniżej. Rozwiązanie Po likwidacji połączenia szeregowego rezystorów ( i oraz i ) należy zastosować transformację trójkąt-gwiazda lub gwiazda-trójkąt w odniesieniu do wybranych trzech rezystorów obwodu, a następnie wykorzystać uproszczenia wynikające z powstałych połączeń szeregowych i równoległych w obwodzie. Po wykonaniu tych działań otrzymuje się . |