PEE Moduł 1: Różnice pomiędzy wersjami
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 357: | Linia 357: | ||
|valign="top"|'''Transfiguracja gwiazda-trójkąt i trójkąt-gwiazda''' | |valign="top"|'''Transfiguracja gwiazda-trójkąt i trójkąt-gwiazda''' | ||
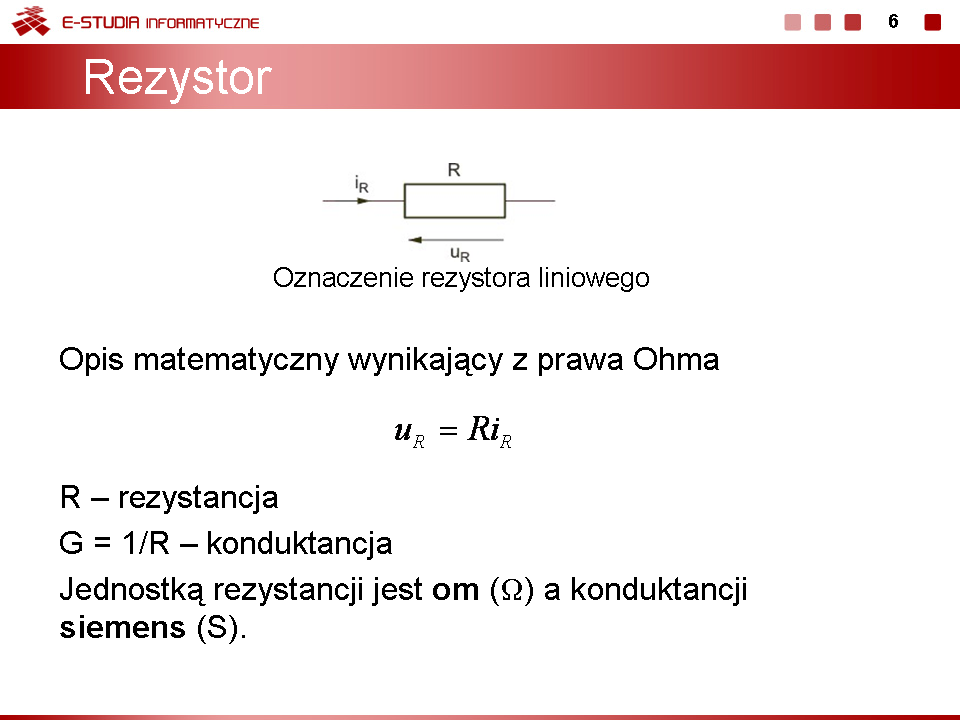
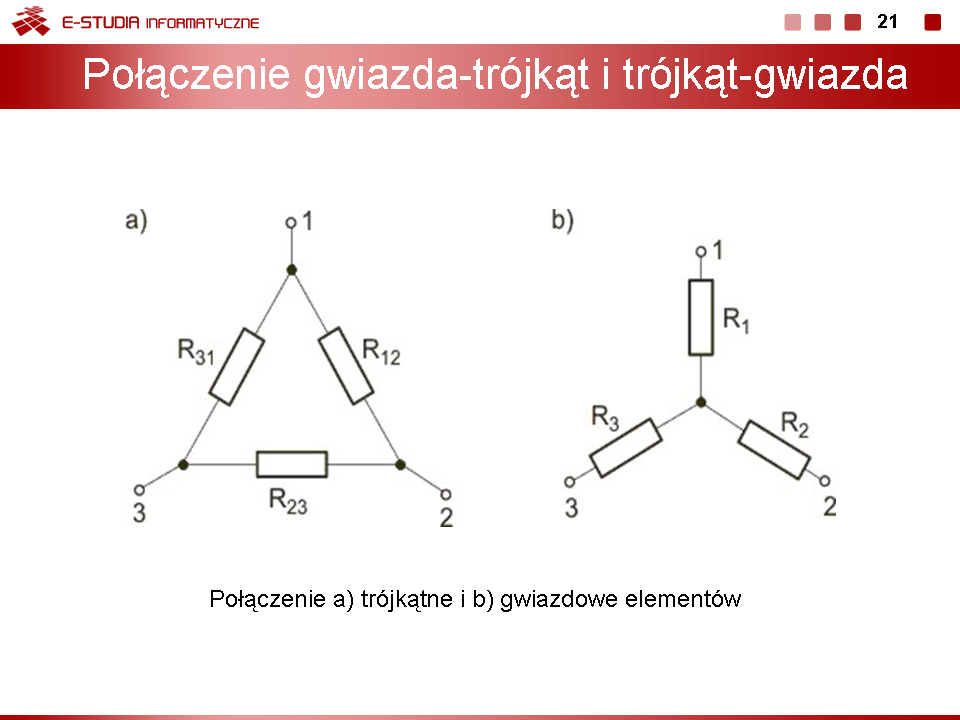
Operowanie uproszczonym schematem wynikającym z połączenia szeregowego i równoległego elementów jest najwygodniejszym sposobem redukcji obwodu. W przypadku gdy nie ma elementów połączonych szeregowo czy równolegle możliwe jest dalsze uproszczenie przez zastosowanie przekształcenia gwiazda-trójką lub trójkąt-gwiazda. Oznaczenia elementów obwodu trójkąta i gwiazdy są przedstawione na rysunku obok | Operowanie uproszczonym schematem wynikającym z połączenia szeregowego i równoległego elementów jest najwygodniejszym sposobem redukcji obwodu. W przypadku gdy nie ma elementów połączonych szeregowo czy równolegle możliwe jest dalsze uproszczenie przez zastosowanie przekształcenia gwiazda-trójką lub trójkąt-gwiazda. Oznaczenia elementów obwodu trójkąta i gwiazdy są przedstawione na rysunku obok. | ||
|} | |} | ||
| Linia 368: | Linia 368: | ||
: <math>R_{12}=R_1+R_2+{R_1R_2 \over R_3}</math> | : <math>R_{12}=R_1+R_2+{R_1R_2 \over R_3}</math> | ||
: <math>R_{23}=R_2+R_3+{R_2R_3 \over R_1}</math> | : <math>R_{23}=R_2+R_3+{R_2R_3 \over R_1}</math> | ||
: <math>R_{31}=R_3+R_1+{R_3R_1 \over R_2}</math> | : <math>R_{31}=R_3+R_1+{R_3R_1 \over R_2}</math> | ||
|} | |} | ||
| Linia 378: | Linia 380: | ||
|valign="top"|Podobnie przy zamianie trójkąta na gwiazdę rezystancje gwiazdy muszą spełniać warunki | |valign="top"|Podobnie przy zamianie trójkąta na gwiazdę rezystancje gwiazdy muszą spełniać warunki | ||
: <math>R_1=\frac{R_{12}R_{31}}{R_{12}R_{23}R_{31}}</math> | : <math>R_1=\frac{R_{12}R_{31}}{R_{12}+R_{23}+R_{31}}</math> | ||
: <math>R_2=\frac{R_{23}R_{12}}{R_{12}R_{23}R_{31}}</math> | |||
: <math>R_3=\frac{R_{31}R_{23}}{R_{12}R_{23}R_{31}}</math> | : <math>R_2=\frac{R_{23}R_{12}}{R_{12}+R_{23}+R_{31}}</math> | ||
: <math>R_3=\frac{R_{31}R_{23}}{R_{12}+R_{23}+R_{31}}</math> | |||
Przekształcenia równoważne obwodu wykorzystujące reguły połączenia szeregowego, równoległego oraz przekształcenia gwiazda-trójkąt i trójkąt-gwiazda umożliwiają dalszą redukcję tego obwodu i po wykonaniu odpowiedniej liczby przekształceń sprowadzenie go do pojedynczego elementu zastępczego. | Przekształcenia równoważne obwodu wykorzystujące reguły połączenia szeregowego, równoległego oraz przekształcenia gwiazda-trójkąt i trójkąt-gwiazda umożliwiają dalszą redukcję tego obwodu i po wykonaniu odpowiedniej liczby przekształceń sprowadzenie go do pojedynczego elementu zastępczego. | ||
Wersja z 07:56, 24 sie 2006

|

|
Wykład 1 Podstawowe prawa obwodów elektrycznych |
|
| Zadania sprawdzające
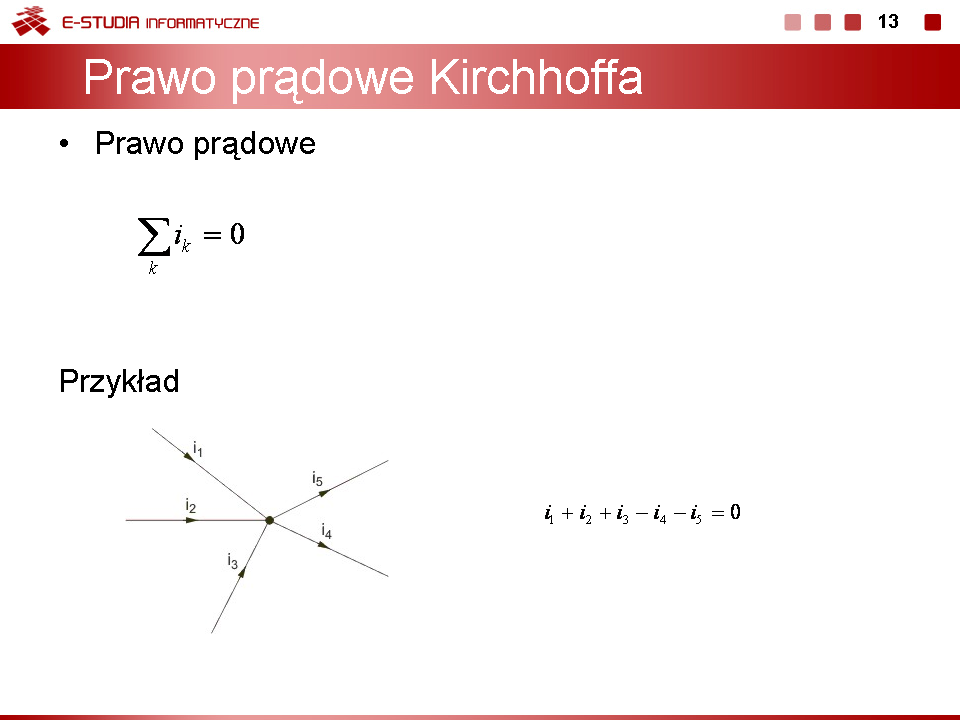
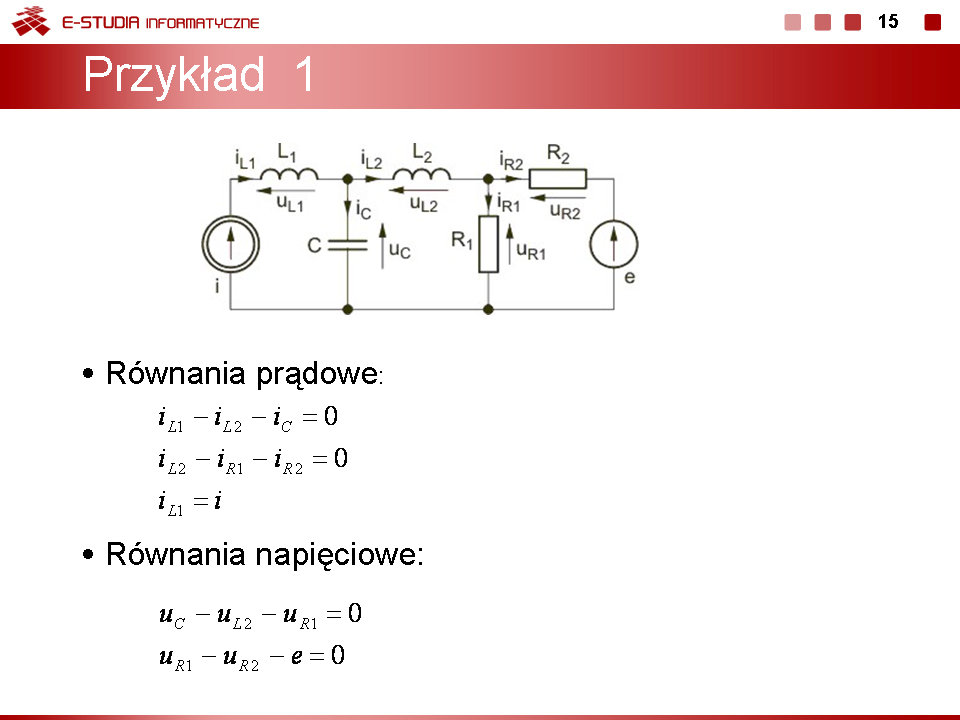
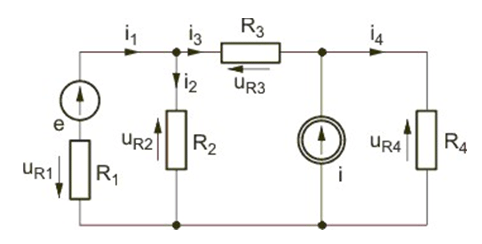
Stosując prawa Kirchhoffa wyznaczyć prądy w obwodzie przedstawionym na rysunku poniżej, jeśli , , , , a wartości źródeł są następujące: , . Rozwiązanie Korzystając z praw Kirchhoffa otrzymuje się układ równań opisujących obwód w postaci Po wstawieniu wartości liczbowych parametrów i rozwiązaniu układu równań otrzymuje się: , , oraz .
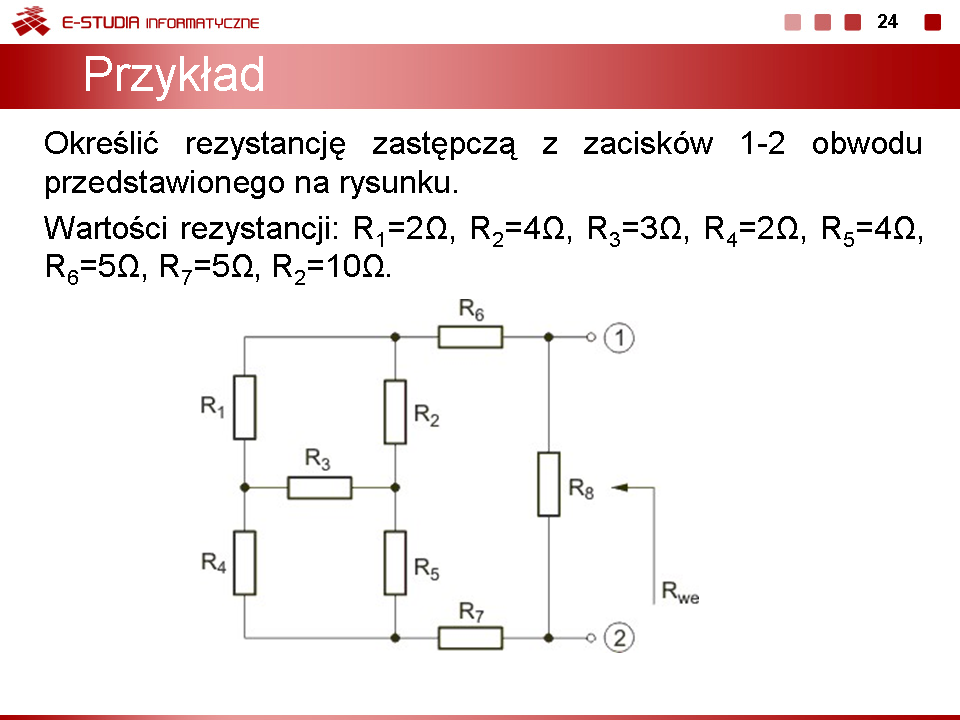
Wyznaczyć rezystancję wypadkową obwodu przedstawionego na rysunku poniżej. Rozwiązanie Po likwidacji połączenia szeregowego rezystorów ( i oraz i ) należy zastosować transformację trójkąt-gwiazda lub gwiazda-trójkąt w odniesieniu do wybranych trzech rezystorów obwodu, a następnie wykorzystać uproszczenia wynikające z powstałych połączeń szeregowych i równoległych w obwodzie. Po wykonaniu tych działań otrzymuje się . |