PEE Moduł 1: Różnice pomiędzy wersjami
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 295: | Linia 295: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M1_Slajd17.png]] | |valign="top" width="500px"|[[Grafika:PEE_M1_Slajd17.png]] | ||
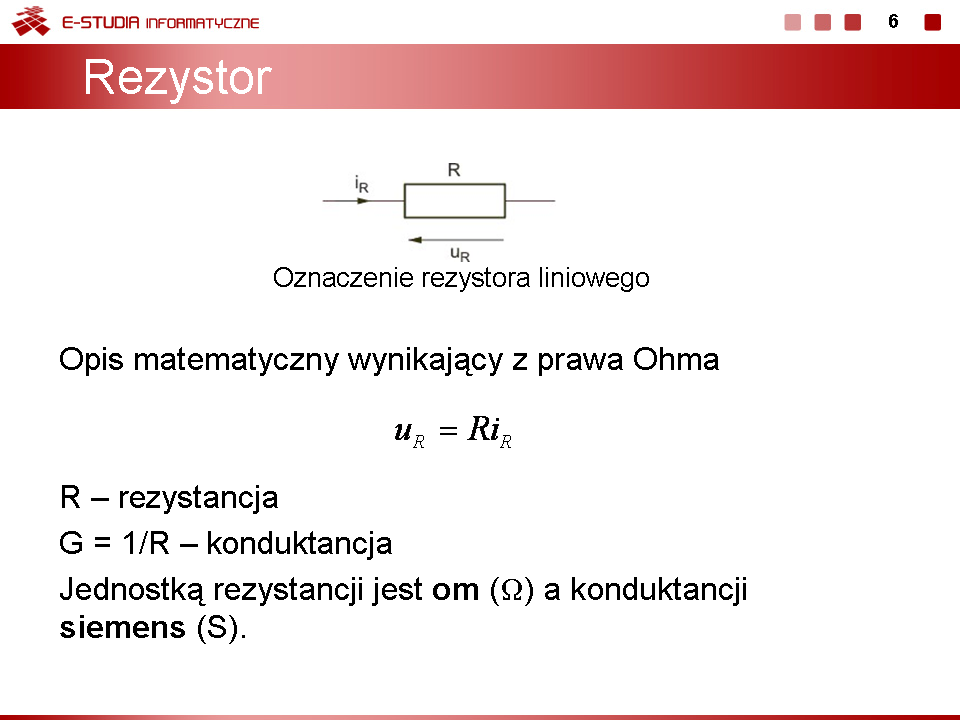
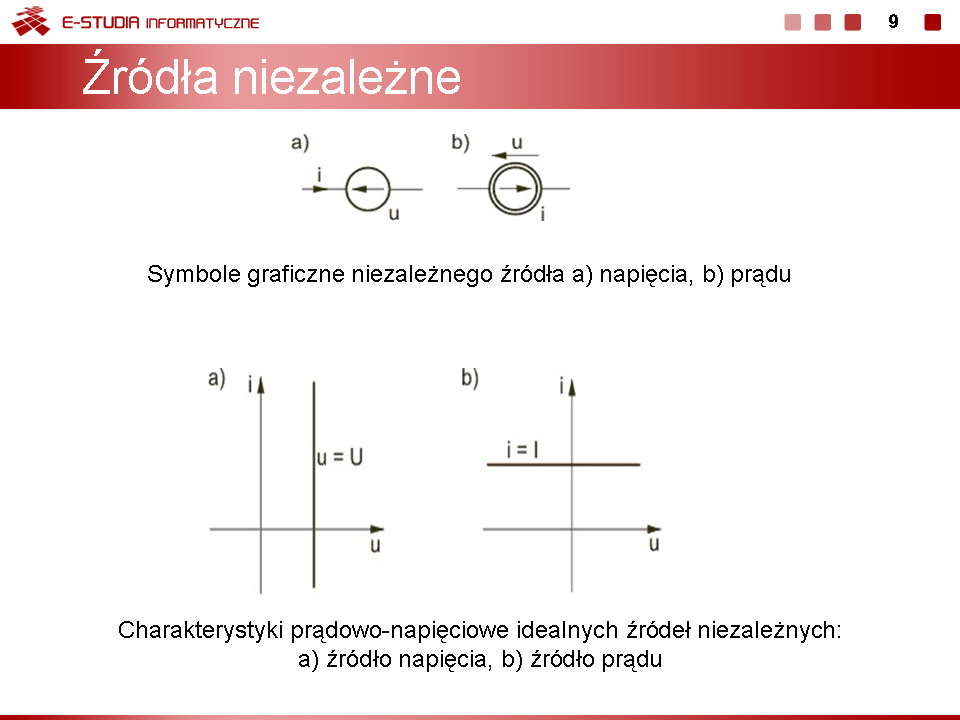
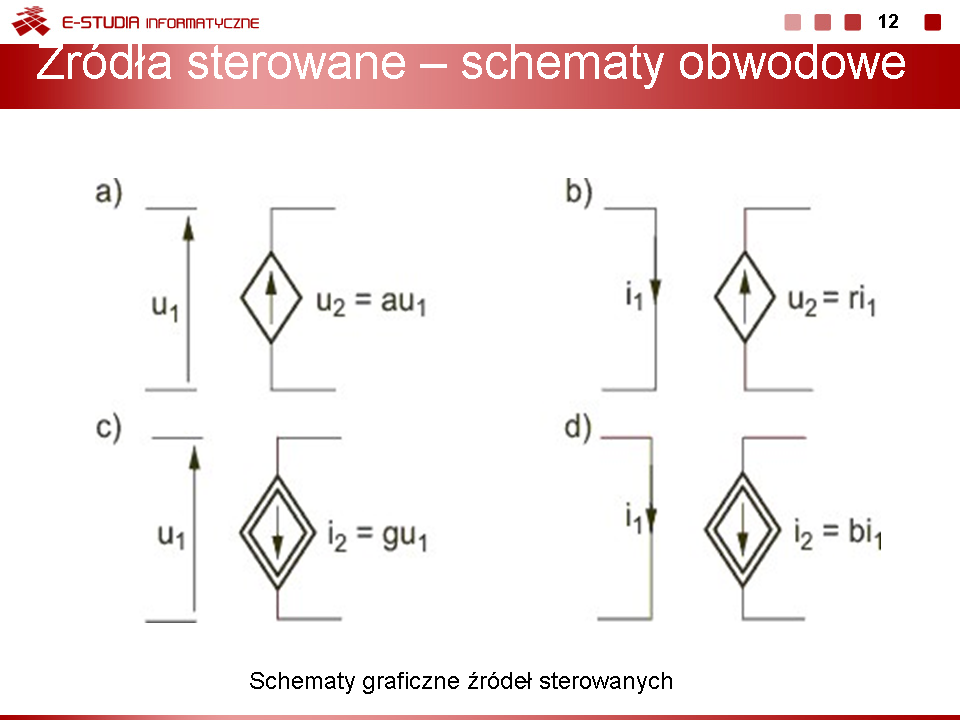
|valign="top"|''' | |valign="top"|'''Podstawowe rodzaje połączeń elementów''' | ||
W analizie obwodów elektrycznych ważną rolę odgrywa upraszczanie struktury obwodu, polegające na zastępowaniu wielu elementów połączonych szeregowo lub równolegle poprzez jeden element zastępczy. Umożliwia to zmniejszenie liczby równań w opisie obwodu i uproszczenie etapu rozwiązania tych równań. Wyróżnić można cztery podstawowe rodzaje połączeń elementów, do których stosuje się przekształcenie. Są to: | W analizie obwodów elektrycznych ważną rolę odgrywa upraszczanie struktury obwodu, polegające na zastępowaniu wielu elementów połączonych szeregowo lub równolegle poprzez jeden element zastępczy. Umożliwia to zmniejszenie liczby równań w opisie obwodu i uproszczenie etapu rozwiązania tych równań. Wyróżnić można cztery podstawowe rodzaje połączeń elementów, do których stosuje się przekształcenie. Są to: | ||
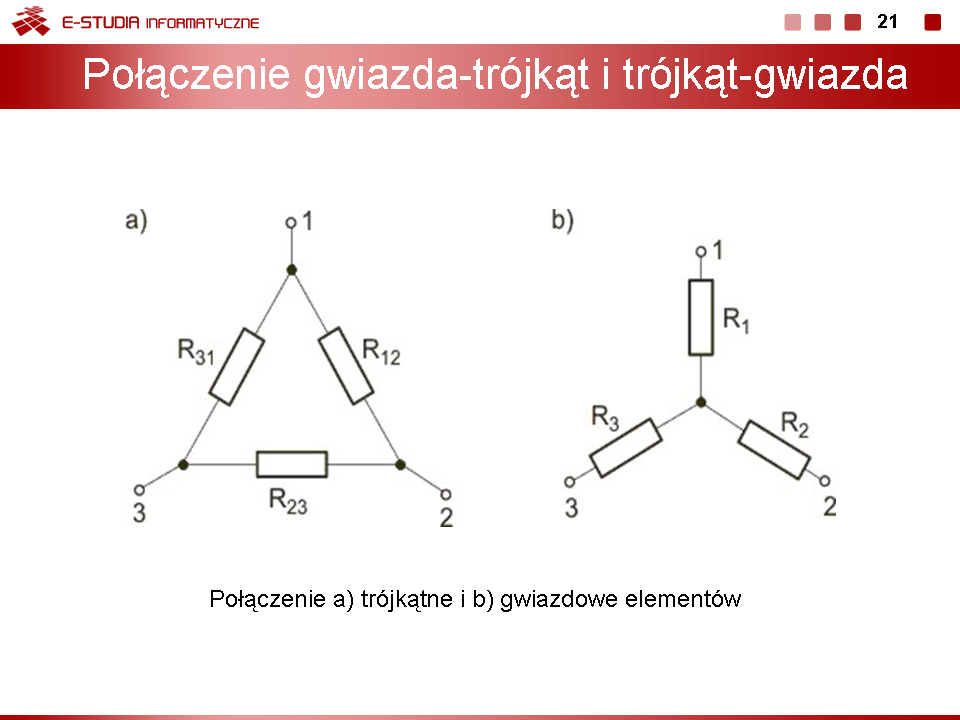
| Linia 305: | Linia 305: | ||
*połączenie gwiazdowe | *połączenie gwiazdowe | ||
*połączenie trójkątne | *połączenie trójkątne | ||
|} | |} | ||
| Linia 315: | Linia 315: | ||
|valign="top"|'''Układ połączenia szeregowego elementów''' | |valign="top"|'''Układ połączenia szeregowego elementów''' | ||
W połączeniu szeregowym elementów koniec jednego elementu jest bezpośrednio połączony z początkiem następnego. | W połączeniu szeregowym elementów koniec jednego elementu jest bezpośrednio połączony z początkiem następnego. Rysunek na slajdzie obok przedstawia schemat ogólny połączenia szeregowego rezystorów. | ||
Prąd każdego elementu obwodu jest jednakowy i równy <math>i\,</math>, natomiast napięcie na zaciskach zewnętrznych obwodu jest równe sumie napięć poszczególnych elementów tworzących połączenie. Napięciowe równanie Kirchhoffa dla obwodu (z rysunku na slajdzie | Prąd każdego elementu obwodu jest jednakowy i równy <math>i\,</math>, natomiast napięcie na zaciskach zewnętrznych obwodu jest równe sumie napięć poszczególnych elementów tworzących połączenie. Napięciowe równanie Kirchhoffa dla obwodu (z rysunku na slajdzie obok) przyjmuje więc postać: | ||
: <math>u=(R_1+R_2+...+R_N)i</math> | : <math>u=(R_1+R_2+...+R_N)i</math> | ||
| Linia 325: | Linia 325: | ||
: <math>R=R_1+R_2+...+R_N</math> | : <math>R=R_1+R_2+...+R_N</math> | ||
otrzymuje się uproszczenie <math>N\,</math> rezystorów połączonych szeregowo do jednego rezystora zastępczego o rezystancji <math>R\,</math> opisanej wzorem na slajdzie | otrzymuje się uproszczenie <math>N\,</math> rezystorów połączonych szeregowo do jednego rezystora zastępczego o rezystancji <math>R\,</math> opisanej wzorem na slajdzie. Rezystancja wypadkowa połączenia szeregowego rezystorów jest równa sumie rezystancji poszczególnych elementów tworzących to połączenie. | ||
|} | |} | ||
| Linia 332: | Linia 332: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M1_Slajd18.png]] | |valign="top" width="500px"|[[Grafika:PEE_M1_Slajd18.png]] | ||
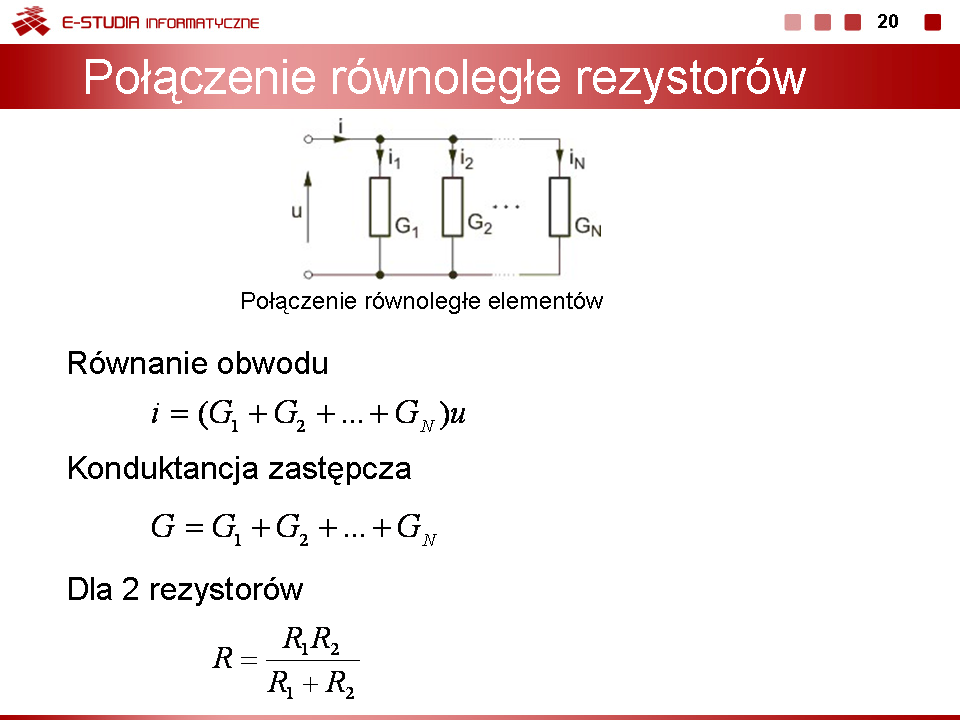
|valign="top"|W połączeniu równoległym początki i końce wszystkich elementów są ze sobą bezpośrednio połączone, jak to pokazano dla elementów rezystancyjnych na rysunku obok | |valign="top"|W połączeniu równoległym początki i końce wszystkich elementów są ze sobą bezpośrednio połączone, jak to pokazano dla elementów rezystancyjnych na rysunku obok. | ||
Z połączenia tego wynika, że napięcie na wszystkich elementach jest jednakowe a prąd wypadkowy jest równy sumie prądów wszystkich elementów obwodu. Prądowe prawo Kirchhoffa dla obwodu z rysunku można więc zapisać w postaci: | Z połączenia tego wynika, że napięcie na wszystkich elementach jest jednakowe a prąd wypadkowy jest równy sumie prądów wszystkich elementów obwodu. Prądowe prawo Kirchhoffa dla obwodu z rysunku można więc zapisać w postaci: | ||
| Linia 342: | Linia 342: | ||
: <math>G=G_1+G_2+...+G_N</math> | : <math>G=G_1+G_2+...+G_N</math> | ||
otrzymuje się uproszczenie <math>N\,</math> rezystorów połączonych równolegle do jednego rezystora zastępczego o konduktancji <math>G\,</math> opisanej wzorem na slajdzie | otrzymuje się uproszczenie <math>N\,</math> rezystorów połączonych równolegle do jednego rezystora zastępczego o konduktancji <math>G\,</math> opisanej wzorem na slajdzie. Jak widać w połączeniu równoległym rezystorów konduktancja wypadkowa jest równa sumie konduktancji poszczególnych rezystorów. | ||
Szczególnie prosty jest wzór na rezystancję zastępczą dla 2 rezystorów połączonych równolegle. W tym przypadku <math>G=G_1+G_2</math>. Uwzględniając, że <math>G=1/R</math> po prostych przekształceniach otrzymuje się | Szczególnie prosty jest wzór na rezystancję zastępczą dla 2 rezystorów połączonych równolegle. W tym przypadku <math>G=G_1+G_2</math>. Uwzględniając, że <math>G=1/R</math> po prostych przekształceniach otrzymuje się | ||
Wersja z 07:55, 24 sie 2006

|

|
Wykład 1 Podstawowe prawa obwodów elektrycznych |
|
| Zadania sprawdzające
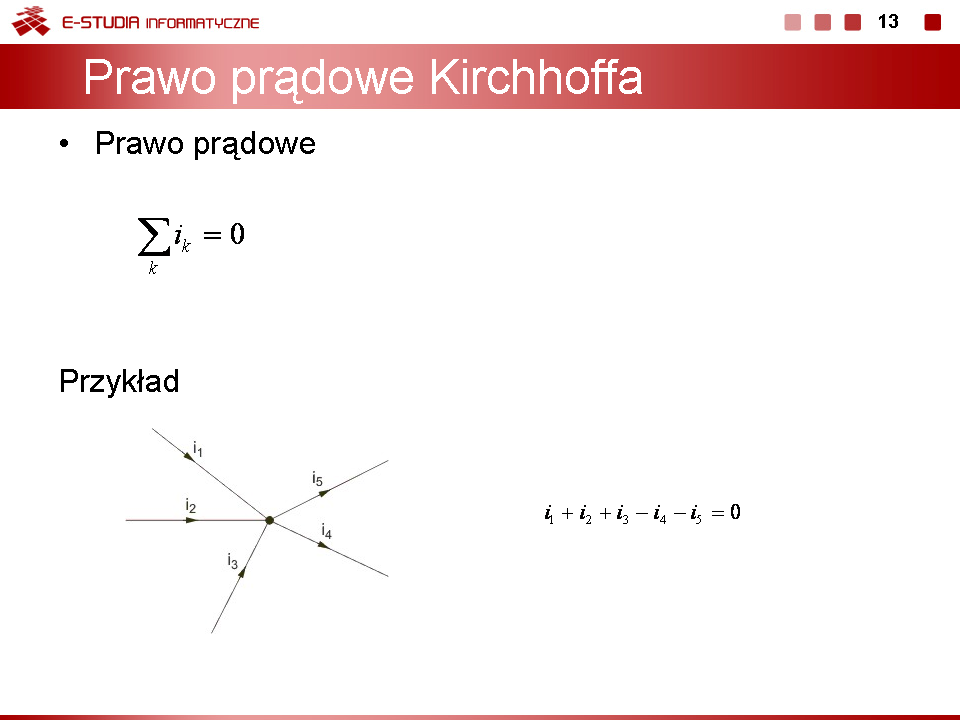
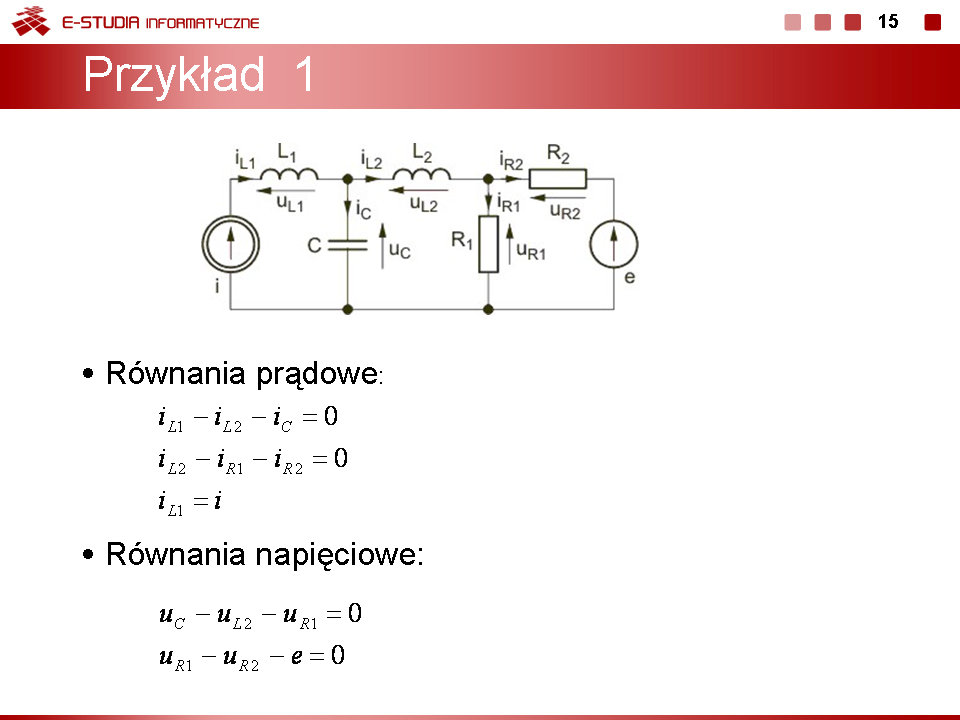
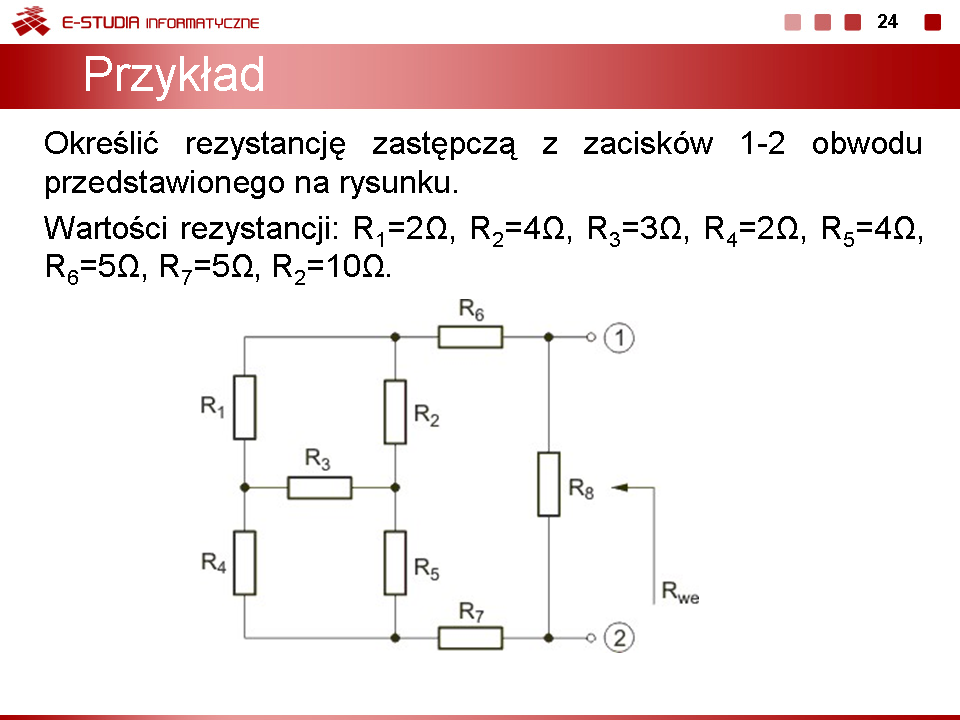
Stosując prawa Kirchhoffa wyznaczyć prądy w obwodzie przedstawionym na rysunku poniżej, jeśli , , , , a wartości źródeł są następujące: , . Rozwiązanie Korzystając z praw Kirchhoffa otrzymuje się układ równań opisujących obwód w postaci Po wstawieniu wartości liczbowych parametrów i rozwiązaniu układu równań otrzymuje się: , , oraz .
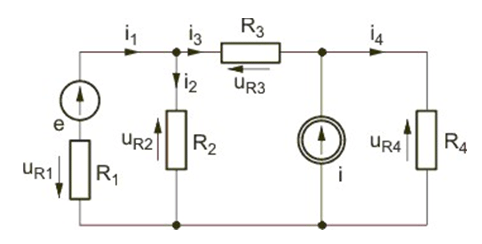
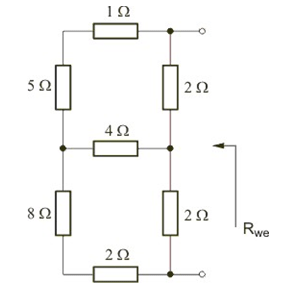
Wyznaczyć rezystancję wypadkową obwodu przedstawionego na rysunku poniżej. Rozwiązanie Po likwidacji połączenia szeregowego rezystorów ( i oraz i ) należy zastosować transformację trójkąt-gwiazda lub gwiazda-trójkąt w odniesieniu do wybranych trzech rezystorów obwodu, a następnie wykorzystać uproszczenia wynikające z powstałych połączeń szeregowych i równoległych w obwodzie. Po wykonaniu tych działań otrzymuje się . |