PEE Moduł 1: Różnice pomiędzy wersjami
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 250: | Linia 250: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M1_Slajd15.png]] | |valign="top" width="500px"|[[Grafika:PEE_M1_Slajd15.png]] | ||
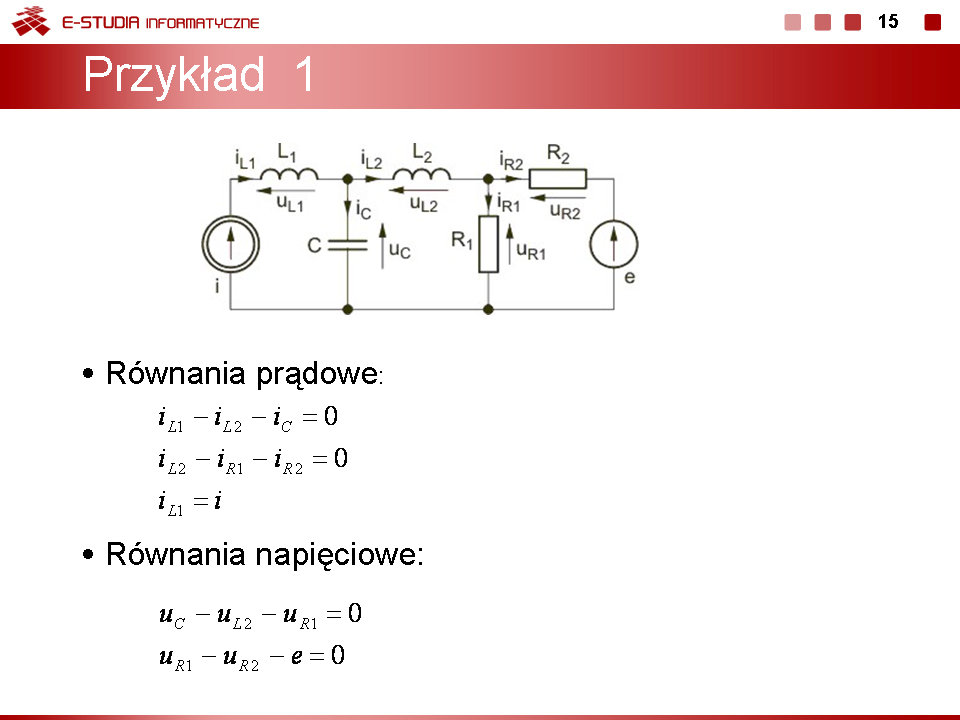
|valign="top"|Sposób tworzenia takiego układu równań pokażemy na przykładzie obwodu ze slajdu obok. | |valign="top"|Sposób tworzenia takiego układu równań pokażemy na przykładzie obwodu ze slajdu obok. | ||
Należy określić prądy gałęziowe obwodu oraz rozkład napięć na elementach w obwodzie rezystancyjnym przedstawionym na rysunku. | |||
|} | |} | ||
| Linia 257: | Linia 258: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M1_Slajd16.png]] | |valign="top" width="500px"|[[Grafika:PEE_M1_Slajd16.png]] | ||
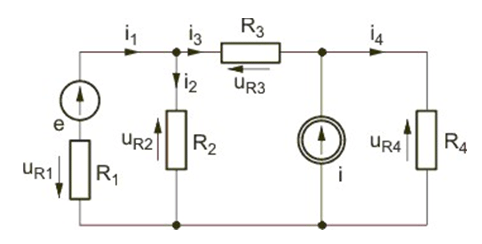
|valign="top"| | |valign="top"|Rozwiązanie obwodu rozpoczynamy od równań Kirchhoffa: | ||
: <math>i_{Z1}-i_1-i_2-i_4=0</math> | : <math>i_{Z1}-i_1-i_2-i_4=0</math> | ||
| Linia 266: | Linia 267: | ||
: <math>u_{R2}-e-u_{R4}=0</math> | : <math>u_{R2}-e-u_{R4}=0</math> | ||
Równania elementów rezystancyjnych: <math>u_{R1}=R_1i_1</math>, <math>u_{R2}=R_2i_2</math>, <math>u_{R3}=R_3i_3</math>, <math>u_{R4}=R_4i_4</math> tworzą wspólnie z równaniami Kirchhoffa następujący układ równań algebraicznych: | Równania elementów rezystancyjnych: <math>u_{R1}=R_1i_1</math>, <math>u_{R2}=R_2i_2</math>, <math>u_{R3}=R_3i_3</math>, <math>u_{R4}=R_4i_4</math> tworzą wspólnie z równaniami Kirchhoffa następujący układ równań algebraicznych: | ||
| Linia 277: | Linia 277: | ||
: <math>R_2i_2-R_4i_4=e</math> | : <math>R_2i_2-R_4i_4=e</math> | ||
Po wstawieniu danych liczbowych do powyższych równań otrzymuje się: | Po wstawieniu danych liczbowych do powyższych równań otrzymuje się: | ||
| Linia 288: | Linia 287: | ||
: <math>2i_2-4i_4=10</math> | : <math>2i_2-4i_4=10</math> | ||
W wyniku rozwiązania tego układu równań otrzymuje się: <math>i_1 = 3,187A</math>, <math>i_2 = 0,875A</math>, <math>i_3 = 3,812A</math> oraz <math>i_4 = -2,062A</math>. Łatwo sprawdzić przez podstawienie obliczonych wartości do układu równań, że bilans prądów w każdym węźle oraz bilans napięć w każdym oczku obwodu jest zerowy. | W wyniku rozwiązania tego układu równań otrzymuje się: <math>i_1 = 3,187A</math>, <math>i_2 = 0,875A</math>, <math>i_3 = 3,812A</math> oraz <math>i_4 = -2,062A</math>. Łatwo sprawdzić przez podstawienie obliczonych wartości do układu równań, że bilans prądów w każdym węźle oraz bilans napięć w każdym oczku obwodu jest zerowy. | ||
Wersja z 07:42, 24 sie 2006

|

|
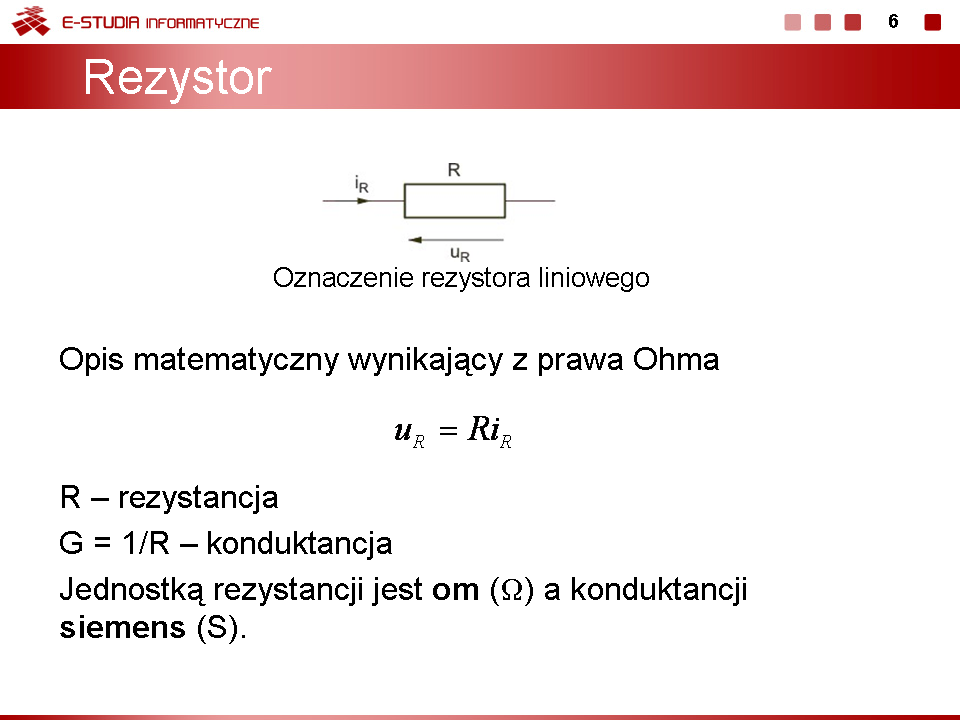
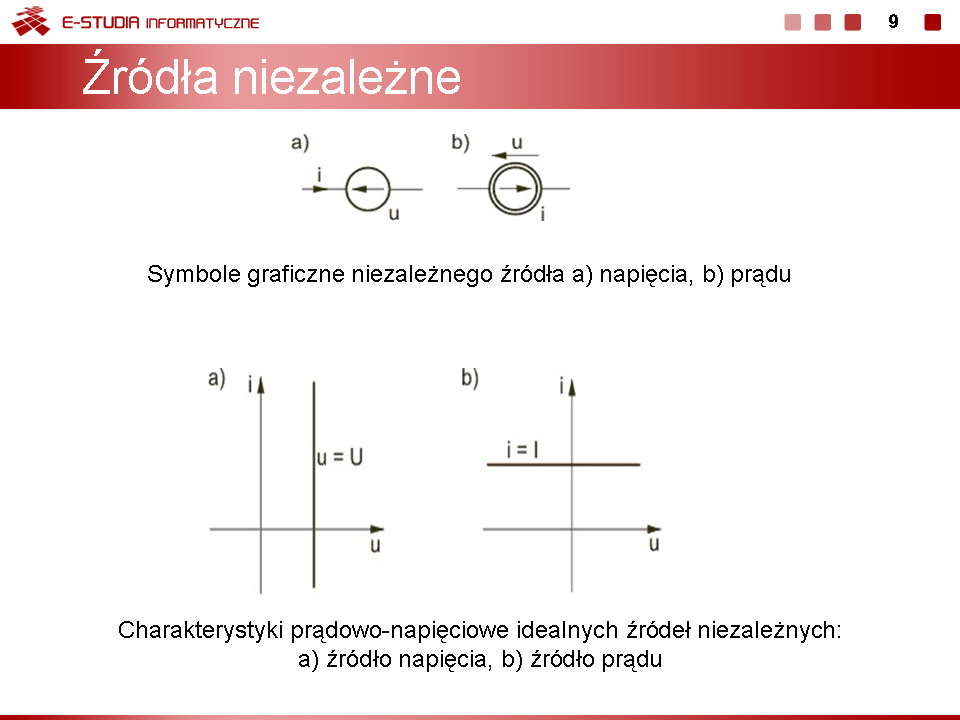
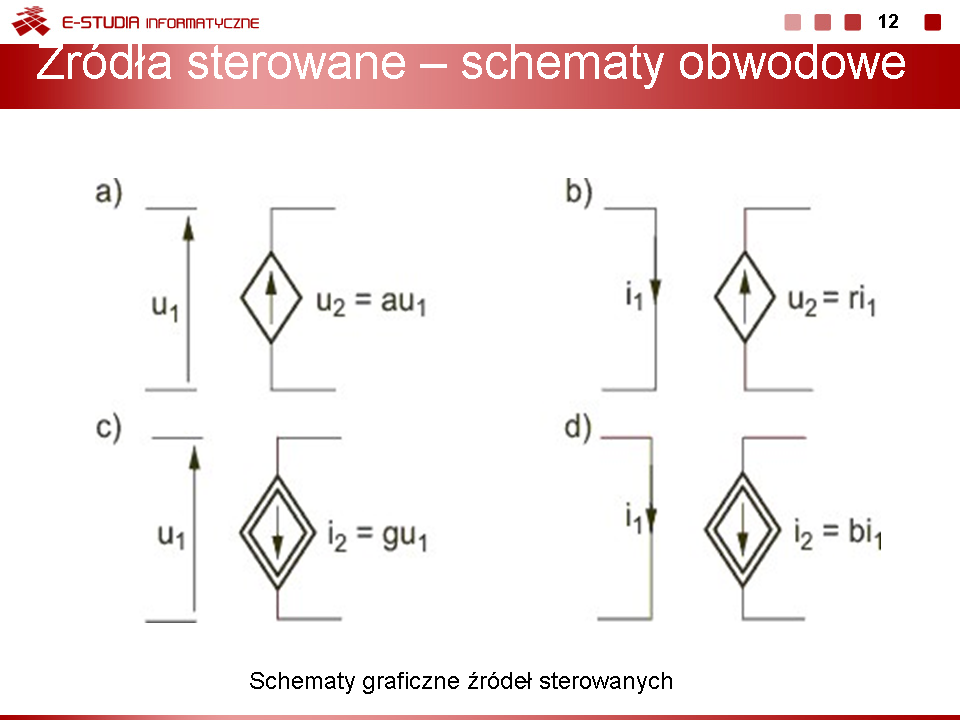
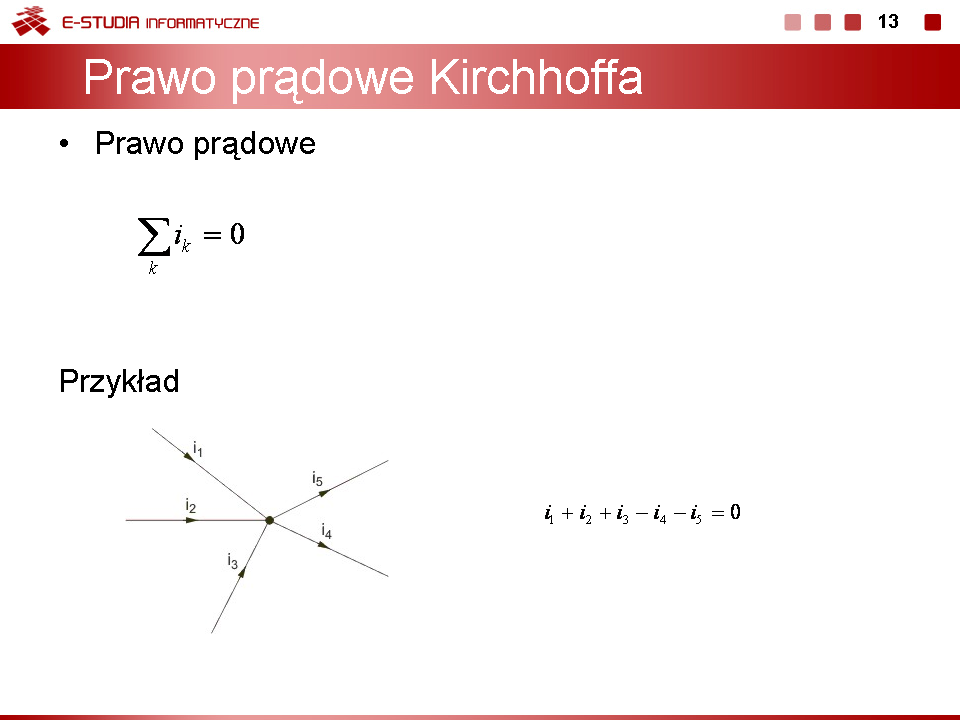
Wykład 1 Podstawowe prawa obwodów elektrycznych |
|
| Zadania sprawdzające
Stosując prawa Kirchhoffa wyznaczyć prądy w obwodzie przedstawionym na rysunku poniżej, jeśli , , , , a wartości źródeł są następujące: , . Rozwiązanie Korzystając z praw Kirchhoffa otrzymuje się układ równań opisujących obwód w postaci Po wstawieniu wartości liczbowych parametrów i rozwiązaniu układu równań otrzymuje się: , , oraz .
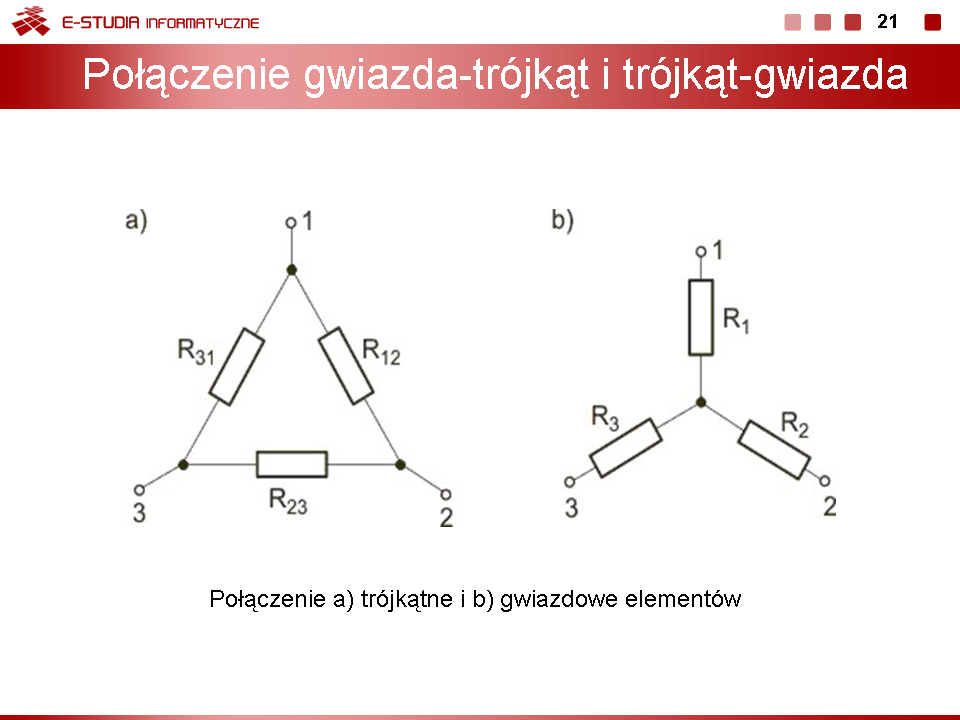
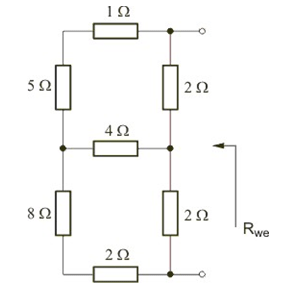
Wyznaczyć rezystancję wypadkową obwodu przedstawionego na rysunku poniżej. Rozwiązanie Po likwidacji połączenia szeregowego rezystorów ( i oraz i ) należy zastosować transformację trójkąt-gwiazda lub gwiazda-trójkąt w odniesieniu do wybranych trzech rezystorów obwodu, a następnie wykorzystać uproszczenia wynikające z powstałych połączeń szeregowych i równoległych w obwodzie. Po wykonaniu tych działań otrzymuje się . |