PEE Moduł 1: Różnice pomiędzy wersjami
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 228: | Linia 228: | ||
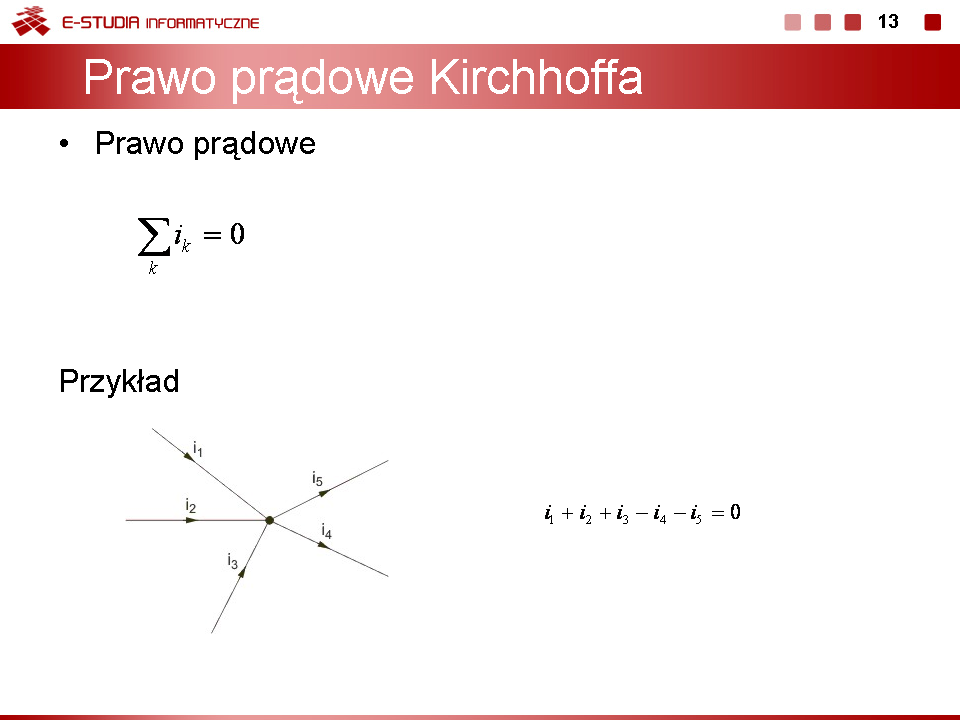
|valign="top"|''Przykład'' | |valign="top"|''Przykład'' | ||
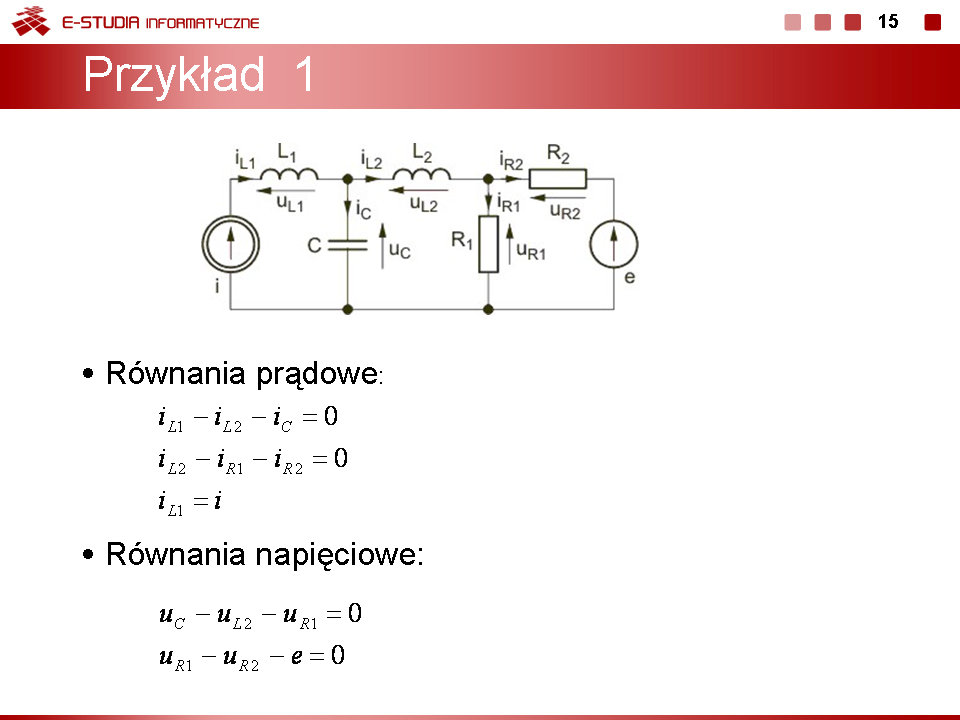
Napiszmy równania Kirchhoffa dla obwodu z rysunku na slajdzie | Napiszmy równania Kirchhoffa dla obwodu z rysunku na slajdzie obok. | ||
Zgodnie z prawami Kirchhoffa równania obwodu przyjmą następującą postać: | Zgodnie z prawami Kirchhoffa równania obwodu przyjmą następującą postać: | ||
| Linia 243: | Linia 243: | ||
Przedstawiony tu układ równań jest wystarczający do uzyskania wszystkich innych wielkości prądowych bądź napięciowych w obwodzie. Należy go jedynie uzupełnić o równania definicyjne wiążące prąd i napięcie każdego elementu. Po takim uzupełnieniu uzyskuje się pełny opis obwodu a jego rozwiązanie pozwala wyznaczyć rozpływ prądów i rozkład napięć w obwodzie. | Przedstawiony tu układ równań jest wystarczający do uzyskania wszystkich innych wielkości prądowych bądź napięciowych w obwodzie. Należy go jedynie uzupełnić o równania definicyjne wiążące prąd i napięcie każdego elementu. Po takim uzupełnieniu uzyskuje się pełny opis obwodu a jego rozwiązanie pozwala wyznaczyć rozpływ prądów i rozkład napięć w obwodzie. | ||
Szczególnie proste zależności otrzymuje się dla obwodu rezystancyjnego, zawierającego oprócz źródeł wymuszających jedynie rezystory oraz (ewentualnie) źródła sterowane o rzeczywistych współczynnikach sterowania. Dla takich obwodów równania elementów rezystancyjnych są dane w postaci zależności algebraicznych, które wstawione do równań Kirchhoffa pozwalają utworzyć układ równań algebraicznych o liczbie zmiennych równych liczbie równań | Szczególnie proste zależności otrzymuje się dla obwodu rezystancyjnego, zawierającego oprócz źródeł wymuszających jedynie rezystory oraz (ewentualnie) źródła sterowane o rzeczywistych współczynnikach sterowania. Dla takich obwodów równania elementów rezystancyjnych są dane w postaci zależności algebraicznych, które wstawione do równań Kirchhoffa pozwalają utworzyć układ równań algebraicznych o liczbie zmiennych równych liczbie równań. | ||
|} | |} | ||
| Linia 250: | Linia 250: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M1_Slajd15.png]] | |valign="top" width="500px"|[[Grafika:PEE_M1_Slajd15.png]] | ||
|valign="top"| | |valign="top"|Sposób tworzenia takiego układu równań pokażemy na przykładzie obwodu ze slajdu obok. | ||
|} | |} | ||
Wersja z 07:39, 24 sie 2006

|

|
Wykład 1 Podstawowe prawa obwodów elektrycznych |

|
Sposób tworzenia takiego układu równań pokażemy na przykładzie obwodu ze slajdu obok. |
|
| Zadania sprawdzające
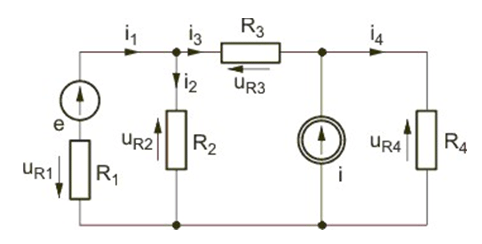
Stosując prawa Kirchhoffa wyznaczyć prądy w obwodzie przedstawionym na rysunku poniżej, jeśli , , , , a wartości źródeł są następujące: , . Rozwiązanie Korzystając z praw Kirchhoffa otrzymuje się układ równań opisujących obwód w postaci Po wstawieniu wartości liczbowych parametrów i rozwiązaniu układu równań otrzymuje się: , , oraz .
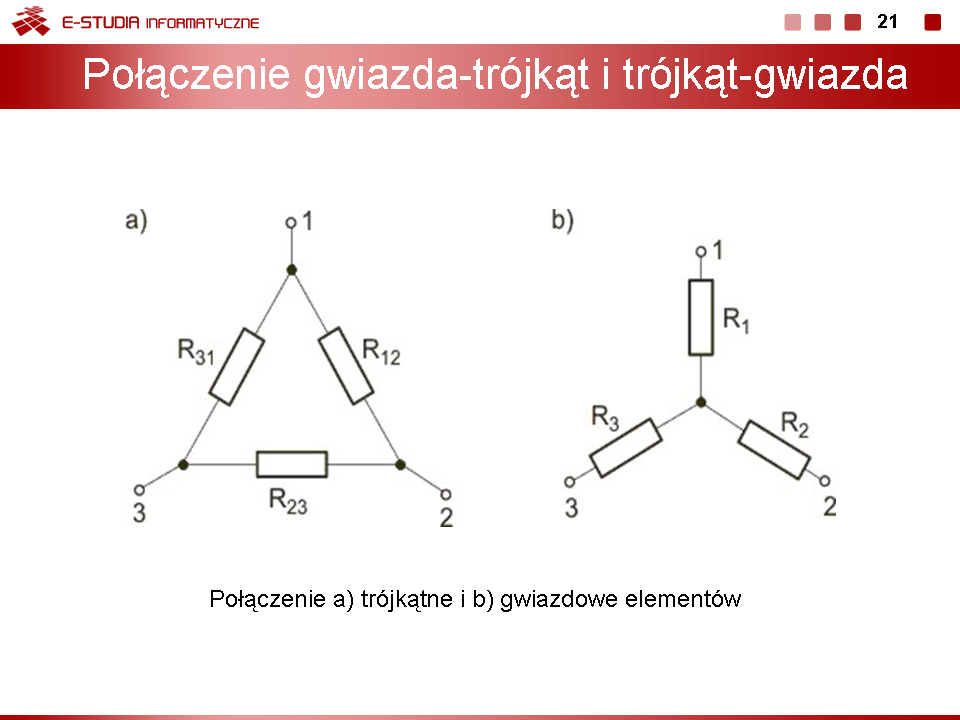
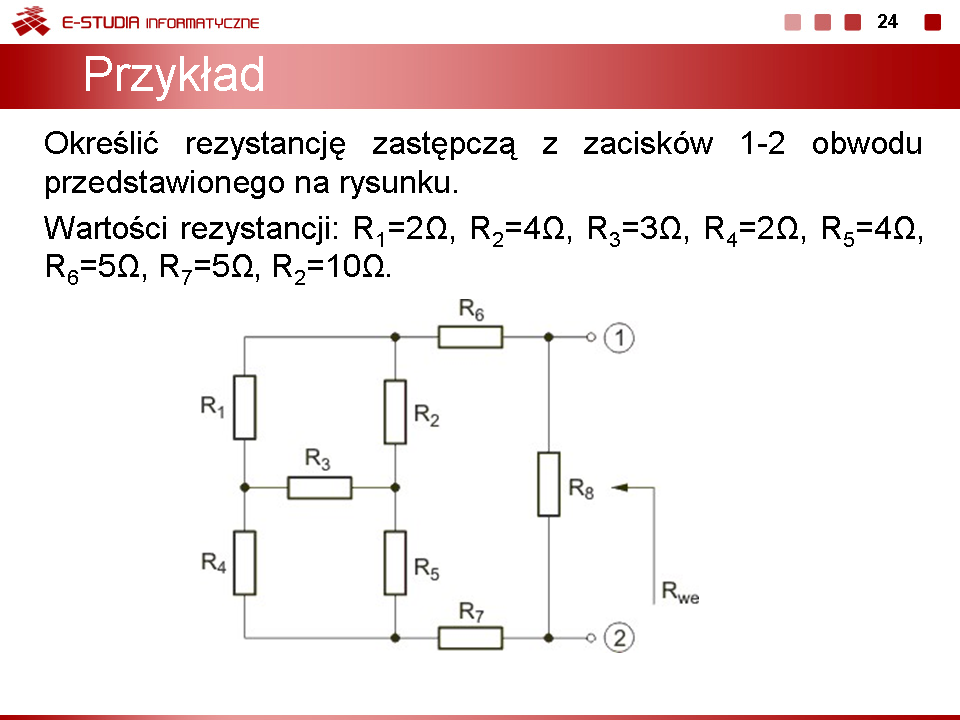
Wyznaczyć rezystancję wypadkową obwodu przedstawionego na rysunku poniżej. Rozwiązanie Po likwidacji połączenia szeregowego rezystorów ( i oraz i ) należy zastosować transformację trójkąt-gwiazda lub gwiazda-trójkąt w odniesieniu do wybranych trzech rezystorów obwodu, a następnie wykorzystać uproszczenia wynikające z powstałych połączeń szeregowych i równoległych w obwodzie. Po wykonaniu tych działań otrzymuje się . |