TTS Moduł 8

Głównymi celami Wykładu 8 jest zapoznanie studiującego z tak ważnymi narzędziami techniki mikrofalowej, jak: wytwarzanie drgań harmonicznych o sinusoidalnym przebiegu i o kontrolowanej amplitudzie i częstotliwości, modulacja i demodulacja sygnałów, detekcja, przemiana częstotliwości.

---

Materiał obu części Wykładu jest obszerny i zapoznaje on studiującego z wieloma nowymi zagadnieniami, technikami i z wielką liczbą nowych pojęć.

---

Na rysunku obok widzimy obraz sygnału o częstotliwości 100MHz otrzymany na ekranie analizatora widma. Sygnał poddany został modulacji amplitudy, a świadczą o tym dwie wstęgi boczne oddalone od prążka fali nośnej o 10 kHz. Jak skonstruowany jest oscylator mikrofalowy, jak go zaprojektować, aby uzyskać sygnał „czysty” w sensie widmowym? Jak skonstruować mechanizm przestrajania i modulacji częstotliwości generatora? Jak przeprowadzić proces modulacji przed wysłaniem sygnału w eter? Jak odzyskać informację po odbiorze sygnału? Oto seria pytań, na które Czytelnik znajdzie odpowiedź w tym wykładzie.

---

O generatorze i warunkach generacji można mówić na kilka sposób, gdyż opracowano wiele modeli opisujących pracę generatora. Jednym z najpopularniejszych jest model dwójnikowy. Na rysunku pokazano ideową strukturę oscylatora, zawierającą trzy podstawowe składniki: element aktywny (np. tranzystor...) umożliwiający powstanie oscylacji, obwód strojenia z rezonatorem, który decyduje o częstotliwości generacji, obciążenie, odbierające wytworzony sygnał. Między rezonatorem a elementem aktywnym a rezonatorem wybrano parę zacisków. W stanie ustalonym sinusoidalnych oscylacji między zaciskami panuje napięcie o amplitudzie zespolonej $U$, oraz płyną prądy o zespolonych amplitudach $I_a$ – w stronę obwodu aktywnego - i $I_c$ w stronę rezonatora. Wymienione prądy łączy oczywisty związek. Na jego podstawie można zdefiniować dwie admitancje: obwodu aktywnego $Y_a$ i obwodu strojenia z rezonatorem $Y_C$ – patrz rysunek. Prowadzi to do admitancyjnego warunku generacji. W powyższym wywodzie pominięto wpływ harmonicznych sygnału generowanego.

---

Analiza bilansu mocy w obwodzie generatora wymaga wprowadzenia pojęcia mocy ujemnej. Moc $P_c$ absorbowana przez rezonator i obciążenie jest dodatnia, jest to moc tracona. Moc $P_a$ jest ujemna, gdy konduktancja Moc $G_a$ jest ujemna. Oznacza to, że konduktancja $G_a$ „pompuje” moc prądu zmiennego do obwodu zewnętrznego. Warunek bilansu mocy jest spełniony w stanie ustalonym generacji. Jednak w stanie narastania lub gaśnięcie oscylacji suma mocy $P_a+P_C$ jest różne od zera. Aby wyjaśnić ten fakt wygodnie jest przyjąć, że prąd $I_c$ jest w fazie z $U$, co oznacza, że prąd $I_a$ jest przesunięty o $180^{\circ }$ względem $U$. Element aktywny, np. tranzystor, jest nieliniowy, co oznacza, że prąd $|I_a|$ tylko do pewnej granicy jest proporcjonalne do $|U_a|$ . W rezultacie moc $P_a$ jest proporcjonalna do $|U{|}^2$ jedynie dla małych amplitud i przechodzi ze wzrostem $|U|$ przez swoje maksimum. Obwód strojenia jako bierny nie wykazuje nieliniowości i wykres $P_C(|U|)$ jest parabolą. Na rysunku b) pokazano wykresy obu mocy. Punkt przecięcia paraboli $P_C$ z linią mocy $P_a$ określa stan ustalony, w którym spełniony jest bilans mocy. Generację inicjują szumy elementu aktywnego. Dla małych amplitud moc dostarczana przez obwód aktywny przewyższa moc traconą, gdyż $P_a+P_c<0$. Nadwyżka mocy powoduje, że amplituda drgań narasta, wzrasta energia zgromadzona w polu elektromagnetycznym obwodu rezonansowego. Proces narastania amplitudy trwa tak długo, aż spełniony zostanie bilans mocy. Gdy $P_a+P_c<0$ , drgania gasną. Na rysunku c) pokazano inny, typowy dla generatora obcowzbudnego, przebieg mocy $P_a$. Proces samowzbudzenia nie nastąpi, ponieważ dla małych napięć bilans mocy jest niekorzystny, moc tracona przewyższa moc oddaną przez obwód aktywny. Doprowadzenie mocy z zewnątrz może wprowadzić obwód w stan, gdzie $P_a+P_c<0$. Powstaje pytanie, który z punktów przecięcia charakterystyk, A czy B będzie punktem stabilnych oscylacji. Łatwo zauważyć, że będzie nim punkt B, w którym jest spełniony warunek:

---

Przeanalizujemy dokładniej admitancyjny warunek generacji. Admitancja $Y_a$ zależy od wielu zmiennych: warunków polaryzacji elementu aktywnego $(U_0,I_0)$ , częstotliwości $f$ i amplitudy sygnału oscylacji $|U|$. Dla małych sygnałów $Y_a=Y_{a0}$. Admitancja obwodowa $Y_c$ jest sumą 2 składników: admitancji rezonatora $Y_r$ i admitancji obciążenia $Y_L$ – patrz rysunek. Dla uproszczenia przyjmiemy założenie, że $Y_L$ jest czysto rzeczywiste. Admitancja rezonatora $Y_r$ jest silnie zależna od częstotliwości. Warunek admitancyjny generacji można teraz zapisać jako dwa oddzielne warunki: amplitudy i fazy. Na rysunku pokazano graficzną interpretację admitancyjnego warunku generacji. Linia niebieska to admitancja obwodowa, silnie zależna od częstotliwości, Linia czerwona opisuje zachowanie admitancji obwodu aktywnego. Ze wzrostem amplitudy wartość $Y_a$ zmienia się od $Y_{a0}$ do wartości odpowiadającej punktowi przecięcia. Tak więc położenie punktu przecięcia na linii $Y_a$ określa amplitudę oscylacji, a na linii $Y_C$ częstotliwość oscylacji.

---

Oscylator można przedstawić w ogólnej postaci obwodu zastępczego z rysunku a). Wybieramy wrota w prowadnicy łączącej obwód strojenia z obwodem aktywnym. W ustalonym stanie generacji rozchodzą się fale o amplitudach $U_i$ i $U_r$. W tej wybranej płaszczyźnie określane są ${\mathrm{\Gamma }}_a$ współczynnik odbicia obwodu aktywnego i ${\mathrm{\Gamma }}_c$ współczynnik odbicia obwodu strojenia: Reflektancyjny warunek generacji jest zapisem oczywistego faktu, że jeden współczynnik jest odwrotnością drugiego: Oznaczymy moduły i argumenty obu współczynników odbicia: dla obwodu aktywnego ${\mathrm{\Gamma }}_a=|{\mathrm{\Gamma }}_a|e^{j{\gamma }_a}$ i dla obwodu strojenia ${\mathrm{\Gamma }}_c=|{\mathrm{\Gamma }}_c|e^{j{\gamma }_c}$ . Warunek generacji można zapisać dwoma równościami: warunkiem amplitudy, oraz warunkiem fazy. Współczynnik odbicia obwodu aktywnego ${\mathrm{\Gamma }}_a={\mathrm{\Gamma }}_{a0}(U_0,I_0,\omega )S(|U_r|)$ jest funkcją kilku zmiennych, podobnie jak admitancja $Y_a$. Natomiast współczynnik odbicia obwodu strojenia ${\mathrm{\Gamma }}_S(\omega )$ jest funkcją częstotliwości. Ilustracja warunku generacji na płaszczyźnie zespolonej wymaga wykreślenia zależności ${\mathrm{\Gamma }}_S(\omega )$ i odwrotności $1/{\mathrm{\Gamma }}_a(P)$, co pokazano na rysunku b). Punkt przecięcia wskazuje stan ustalony generacji. Położenie tego punktu na linii ${\mathrm{\Gamma }}_S(\omega )$ wyznacza częstotliwość oscylacji, a na linii $1/{\mathrm{\Gamma }}_a(P)$ wyznacza moc oscylacji.

---

Tranzystor jest uniwersalnym elementem aktywnym, używanym do wzmocnienia i generacji sygnału od kilku Hz do 200 GHz. Wykorzystując wielką aktywność tranzystora opracowano wiele rozmaitych konfiguracji obwodów oscylujących. W pasmie fal mikrofalowych i milimetrowych najlepsze rezultaty uzyskuje się stosując prostą strukturę dwójnikową. W układzie oddzielono część aktywną umożliwiającą spełnienie warunku amplitudy, od części określającą częstotliwość generacji, zwaną obwodem strojenia. Część mocy wyprowadzana na zewnątrz oscylatora reprezentowana jest przez impedancję obciążęnia. Dla układu dwójnikowego najwygodniej oprzeć analizę warunków pracy oscylatora tranzystorowego o reflektancyjny warunek generacji. Określmy przez ${\mathrm{\Gamma }}_{a0}$ - współczynnik odbicia dla małych sygnałów, aby napisać warunek samodzielnego startu oscylacji. Rolą obwodu aktywnego jest uczynić odpowiednio dużym moduł współczynnika odbicia $|{\mathrm{\Gamma }}_{a0}|$ w żądanym pasmie częstotliwości, aby, mimo strat obwodu strojenia, spełnić warunek amplitudy. Decydująca rolę gra obwód sprzężenia, zwykle indukcyjność lub odcinek linii zwartej. Obwód strojenia zapewnia spełnienie warunku fazy, ewentualnie umożliwia przestrajanie, przy możliwie dużej dobroci, aby sygnał był „czysty”. Obwód wyjściowy nie gra zwykle istotnej roli, czasami potrzebny jest do spełnienia warunku szerokopasmowych oscylacji.

---

Przykład: Przygotowano obwód aktywny do pracy w obwodzie oscylatora w pasmie 8 GHz. Wybrano tranzystor FET N325 o częstotliwości granicznej 18 GHz. Elementy obwodu pokazano na rysunku a). Na rysunku b) pokazano wyniki obliczeń współczynnika odbicia ${\mathrm{\Gamma }}_{a0}(f)$ dla obwodu sprzężenia w postaci odcinka linii bezstratnej o $Z_0=150\mathrm{\Omega }$ , dla 3 długości tej linii. W każdym przypadku uzyskano $|S_{11}|$ przekraczające wartość 6 dla środka pasma, co gwarantuje uzyskanie oscylacji.

---

Źródła sygnałów powinny mieć możliwość zmiany, przestrajania częstotliwości generacji. Znane są dwie techniki przestrajania: Przestrajanie mechaniczne dokonywane jest zwykle przez zmianę wymiarów rezonatora, albo też przez wprowadzenie do jego objętości elementu metalowego lub dielektrycznego, zaburzającego pole EM i zmieniającego jego częstotliwość rezonansową. Przestrajanie mechaniczne jest powolne. Przestrajanie elektryczne dokonywane jest przez sprzężenie z rezonatorem elementu o zmiennej reaktancji. Przestrajanie elektryczne pozwala na szybką zmianę częstotliwości oscylacji. W szczególności w zależności od przyjętego rozwiązania rozróżniamy: Przestrajanie napięciowe, najczęściej z użyciem diody waraktorowej o zmiennej pojemności (tzw. VCO - ang. Voltage Control Oscillator). VCO umożliwiają szybką modulację częstotliwości. Przestrajanie prądowe przez zmianę prądu elektromagnesu, w polu magnetycznym którego umieszczono rezonator ferrimagnetyczny (tzw. CCO - ang. Current Control Oscillator). CCOs umożliwiają wobulację, technikę wykorzystywaną w miernictwie mikrofalowym w wobulatorach i syntezerach.

---

Układ generatora wraz ze wzmacniaczem separującym wykonane są zwykle na podłożu ceramicznym, w technologii hybrydowych układów scalonych. Schemat układu generatora pokazano na rysunku. Generator z rezonatorem YIG konstruowany jest zwykle w wersji szerokopasmowej. Pasmo przestrajania jest bardzo duże, $f_{max}/f_{min}\approx 3:1$ ( od 2GHz do 6GHz). Indukcyjność $L_M$ i obwód korygujący zapewniają szerokopasmową „aktywność” warunkującą powstanie oscylacji. $R$ rezonator silnie sprzężony i oddalony o $\theta$ spełnia warunek fazy. Oscylator jest przestrajany przez zmianę prądu cewki elektromagnesu. Szybkość przestrajania ograniczona jest dużą indukcyjnością cewki elektromagnesu; z tego powodu oscylatory tego typu stosowane są w wobulatorach, czyli wolno przestrajanych generatorach pomiarowych.

---

Na rysunku pokazano podstawową strukturę oscylatora tranzystorowego z diodą waraktorową. Obwód rezonansowy, z którym sprzężony jest waraktor może być konstruowany w rozmaity sposób. Może to być obwód typu LC ze skupioną indukcyjnością, może też zawierać elementy linii długiej. Obwód taki nadaje się szczególnie do wykonania w technologii układów scalonych hybrydowych albo monolitycznych. Szybkość przestrajania generatorów z diodami waraktorowymi jest bardzo duża. Częstotliwość oscylacji może być kontrolowana napięciem polaryzacji diody waraktorowej, co daje możliwość modulacji częstotliwości, zarówno analogowej jak i cyfrowej. Możliwość tą należy mieć na uwadze, gdyż jest to praktycznie jedyny sposób na modulację częstotliwości fali nośnej przez bezpośrednią ingerencję w warunek generacji. Modulację amplitudy albo fazy sygnału wykonuje się poza układem oscylatora. Układy generatorów projektowane są zwykle z następnym stopniem wzmacniacza pełniącego rolę separatora pracy oscylatora od zmian obciążenia.

---

Pokazana na ryunku struktura obwodu generatora jest prosta. Rolę indukcyjności $L$ w obwodzie sprzężenia pełni linia zwarta na końcu. Odległość elektryczna $\theta$ rezonatora od tranzystora może być fizycznie zmieniana przesuwem walca dielektrycznego tworzącego rezonator. Właściwy dobór tej odległości pozwala spełnić warunek fazy. Przestrajanie mechaniczne rezonatora dielektrycznego w granicach 10% można zrealizować przez zbliżanie denka metalowego, lub innego dielektryka. Przestrajaniu rezonatota towarzyszy przestrajanie oscylatora. Możliwe jest także przestrajanie elektryczne, waraktorem sprzężonym z linią, w granicach 0,1%. Rozwiązanie to stosuje się do specjalnych zastosowań generatorów przeznaczonych do pracy w układach stabilizacji fazowej.

---

W obszarze zastosowań telekomunikacyjnych (telefonia, radio, telewizja, telewizja satelitarna, itp.) wielokrotnie rozwiązywany jest problem transmisji informacji z punktu do punktu, lub z punktu do wielu punktów. Sama informacja zapisana jest zwykle w postaci sygnału elektrycznego, ale nie przesyłamy jej bezpośrednio, lecz używamy do tego celu fali nośnej, którą modulujemy sygnałem zawierającym informację. Tak więc zapamiętajmy: Fala nośna jest sygnałem elektrycznym, najczęściej sinusoidalnym, poddawanym procesowi modulacji. Fala modulująca jest sygnałem zawierającym informację, użytym do kontroli/modulacji fali nośnej. Fala zmodulowana to końcowy efekt procesu modulacji fali nośnej przez falę modulującą. Fala zmodulowana przesyłana jest następnie od nadajnika do odbiornika. W odbiorniku odebrany sygnał poddawany jest często złożonym procesom. Ich celem jest odzyskanie informacji. Pomijając w tym momencie konieczne wielokrotne wzmacnianie odebranego sygnału, to procesy usuwania fali nośnej i odzyskiwania informacji/fali modulującej nazywamy demodulacją. Podstawowe rodzaje modulacji stosowane przy „zapisywaniu” informacji na falę nośną to: modulacja amplitudy, modulacja kąta, modulacja częstotliwości, modulacja fazy, modulacja impulsowa Ze względu na sposób zapisu informacji mówimy ponadto o: modulacji analogowej modulacji cyfrowej. Informacja, taka jak zapis dźwięku czy też obrazu, może być przekształcona do formy cyfrowej, jako ciąg liczb najczęściej w postaci binarnej. Dlatego modulacja cyfrowa jest coraz powszechniej stosowana.

---

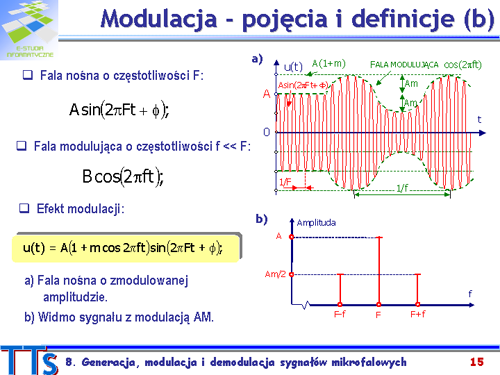
Obiektem modulacji jest fala nośna, charakteryzowana wartościami amplitudy $A$, częstotliwości $F$ i fazy $\varphi$. Fala modulująca opisana jest wartościami amplitudy B i częstotliwości $f<<F$. Informację niesie zwykle przebieg $B(t)$ i $f(t)$, np. w przypadku rejestracji głosu. Efektem modulacji jest fala $u(t)$ o amplitudzie zmieniającej się z częstotliwością $f$ , współczynnik $m\approx B$ jest nazywany wskaźnikiem modulacji. Otrzymana zależność jest sumą trzech składników, które rozpoznajemy jako: falę nośną- $\frac{Am}{2}sin[2\pi (F-f)t+\varphi ]$ wstęgę górną, $Asin(2\pi Ft+\varphi )$ , wstęgę dolną, $Asin(2\pi Ft+\varphi )$ . Na rysunku a) pokazano przebieg czasowy $u(t)$ sygnału o zmodulowanej amplitudzie. Pierwszy fragment wykresu przedstawia czystą falę nośna. Drugi odcinek to fala nośna zmodulowana sygnałem o stałej amplitudzie Am i częstotliwości $f$. Na rysunku b) pokazano charakterystykę widmową sygnału o zmodulowanej amplitudzie. Wysokość wstęg bocznych, dolnej i górnej zależy od głębokości modulacji $m$.

---

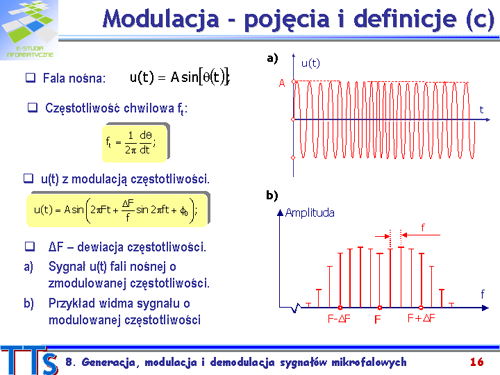
Bardzo chętnie stosowanym rodzajem modulacji jest modulacja częstotliwości. Ten rodzaj modulacji wraz z i modulacją fazy należą do tzw. modulacji kąta. W tym przypadku amplituda $A$ jest stała, a modulowany jest kąt $\varphi (t)$. W przypadku modulacji częstotliwości częstotliwość chwilowa $f_t(t)$ zmienia się wokół wartości średniej $F$. Maksymalne odchylenie $\mathrm{\Delta }F\approx B$ częstotliwości chwilowej $f_t$ od wartości średniej $F$ nazywane jest szczytową dewiacją częstotliwości. Na rysunku a) pokazano przykład przebiegu $u(t)$ zgodnej z powyższą zależnością. Po rozwinięciu zależności na $u(t)$ w szereg Fouriera otrzymuje się nieskończenie wiele składowych, wstęg bocznych wokół częstotliwości $F$ fali nośnej. Amplituda n-tej wstęgi bocznej jest proporcjonalna do $A{J}_n(\mathrm{\Delta }F/f)$. Pojawia się tutaj funkcja Bessela n-tego rzędu, od parametru $\mathrm{\Delta }F/f$. Rzut oka na wykresy rodziny funkcji Bessela pozwala wyciągnąć wniosek, że amplitudy kolejnych składowych szybko maleją ze wzrostem $n$ .