TTS Moduł 8: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 43: | Linia 43: | ||
* obciążenie, odbierające wytworzony sygnał. | * obciążenie, odbierające wytworzony sygnał. | ||
Między rezonatorem a elementem aktywnym a rezonatorem wybrano parę zacisków. W stanie ustalonym sinusoidalnych oscylacji między zaciskami panuje napięcie o amplitudzie zespolonej <math>U\,</math> , oraz płyną prądy o zespolonych amplitudach <math>I_a\,</math> – w stronę obwodu aktywnego - i <math>I_c \,</math> w stronę rezonatora. | Między rezonatorem a elementem aktywnym a rezonatorem wybrano parę zacisków. W stanie ustalonym sinusoidalnych oscylacji między zaciskami panuje napięcie o amplitudzie zespolonej <math>U\,</math>, oraz płyną prądy o zespolonych amplitudach <math>I_a\,</math> – w stronę obwodu aktywnego - i <math>I_c \,</math> w stronę rezonatora. | ||
Wymienione prądy łączy oczywisty związek. Na jego podstawie można zdefiniować dwie admitancje: obwodu aktywnego <math>Y_a \,</math> i obwodu strojenia z rezonatorem <math>Y_C \,</math> – patrz rysunek. Prowadzi to do '''admitancyjnego warunku generacji'''. | Wymienione prądy łączy oczywisty związek. Na jego podstawie można zdefiniować dwie admitancje: obwodu aktywnego <math>Y_a \,</math> i obwodu strojenia z rezonatorem <math>Y_C \,</math> – patrz rysunek. Prowadzi to do '''admitancyjnego warunku generacji'''. | ||
W powyższym wywodzie pominięto wpływ harmonicznych sygnału generowanego. | W powyższym wywodzie pominięto wpływ harmonicznych sygnału generowanego. | ||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:TTS_M8_Slajd5.png]] | |||
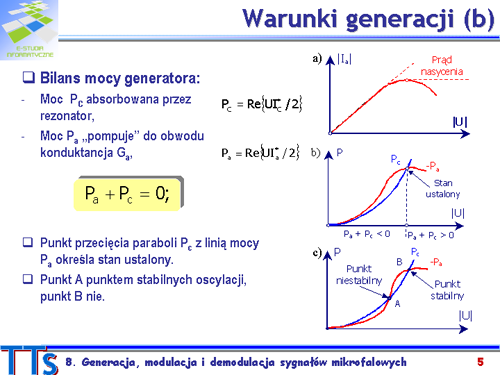
|valign="top"|Analiza bilansu mocy w obwodzie generatora wymaga wprowadzenia pojęcia mocy ujemnej. Moc <math>P_c \,</math> absorbowana przez rezonator i obciążenie jest dodatnia, jest to moc tracona. Moc <math>P_a \,</math> jest ujemna, gdy konduktancja Moc <math>G_a \,</math> jest ujemna. Oznacza to, że konduktancja <math>G_a \,</math> „pompuje” moc prądu zmiennego do obwodu zewnętrznego. | |||
Warunek bilansu mocy jest spełniony w stanie ustalonym generacji. Jednak w stanie narastania lub gaśnięcie oscylacji suma mocy <math>P_a+P_C\,</math> jest różne od zera. Aby wyjaśnić ten fakt wygodnie jest przyjąć, że prąd <math>I_c\,</math> jest w fazie z <math>U\,</math>, co oznacza, że prąd <math>I_a\,</math> jest przesunięty o <math>180^\circ\,</math> względem <math>U\,</math>. Element aktywny, np. tranzystor, jest nieliniowy, co oznacza, że prąd <math>|I_a|\,</math> tylko do pewnej granicy jest proporcjonalne do <math>|U_a|\,</math> . W rezultacie moc <math>P_a \,</math> jest proporcjonalna do <math>|U|^2\,</math> jedynie dla małych amplitud i przechodzi ze wzrostem <math>|U|\,</math> przez swoje maksimum. | |||
Obwód strojenia jako bierny nie wykazuje nieliniowości i wykres <math>P_C(|U|)\,</math> jest parabolą. Na rysunku b) pokazano wykresy obu mocy. Punkt przecięcia paraboli <math>P_C\,</math> z linią mocy <math>P_a\,</math> określa stan ustalony, w którym spełniony jest bilans mocy. | |||
Generację inicjują szumy elementu aktywnego. Dla małych amplitud moc dostarczana przez obwód aktywny przewyższa moc traconą, gdyż <math>P_a+P_c<0\,</math>. Nadwyżka mocy powoduje, że amplituda drgań narasta, wzrasta energia zgromadzona w polu elektromagnetycznym obwodu rezonansowego. Proces narastania amplitudy trwa tak długo, aż spełniony zostanie bilans mocy. Gdy <math>P_a + P_c < 0\,</math> , drgania gasną. | |||
Na rysunku c) pokazano inny, typowy dla generatora obcowzbudnego, przebieg mocy <math>P_a\,</math>. Proces samowzbudzenia nie nastąpi, ponieważ dla małych napięć bilans mocy jest niekorzystny, moc tracona przewyższa moc oddaną przez obwód aktywny. Doprowadzenie mocy z zewnątrz może wprowadzić obwód w stan, gdzie <math>P_a+P_c<0\,</math>. Powstaje pytanie, który z punktów przecięcia charakterystyk, A czy B będzie punktem stabilnych oscylacji. Łatwo zauważyć, że będzie nim punkt B, w którym jest spełniony warunek: | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:TTS_M8_Slajd6.png]] | |||
|valign="top"|Przeanalizujemy dokładniej admitancyjny warunek generacji. Admitancja <math>Y_a\,</math> zależy od wielu zmiennych: warunków polaryzacji elementu aktywnego <math>(U_0, I_0)\,</math> , częstotliwości <math>f\,</math> i amplitudy sygnału oscylacji <math>|U|\,</math>. Dla małych sygnałów <math>Y_a=Y_{a0}\,</math>. Admitancja obwodowa <math>Y_c\,</math> jest sumą 2 składników: admitancji rezonatora <math>Y_r\,</math> i admitancji obciążenia <math>Y_L\,</math> – patrz rysunek. | |||
Dla uproszczenia przyjmiemy założenie, że <math>Y_L\,</math> jest czysto rzeczywiste. Admitancja rezonatora <math>Y_r\,</math> jest silnie zależna od częstotliwości. '''Warunek admitancyjny generacji''' można teraz zapisać jako dwa oddzielne warunki: amplitudy i fazy. | |||
Na rysunku pokazano graficzną interpretację admitancyjnego warunku generacji. Linia niebieska to admitancja obwodowa, silnie zależna od częstotliwości, Linia czerwona opisuje zachowanie admitancji obwodu aktywnego. Ze wzrostem amplitudy wartość <math>Y_a\,</math> zmienia się od <math>Y_{a0}\,</math> do wartości odpowiadającej punktowi przecięcia. Tak więc położenie punktu przecięcia na linii <math>Y_a\,</math> określa amplitudę oscylacji, a na linii <math>Y_C\,</math> częstotliwość oscylacji. | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:TTS_M8_Slajd7.png]] | |||
|valign="top"|Oscylator można przedstawić w ogólnej postaci obwodu zastępczego z rysunku a). Wybieramy wrota w prowadnicy łączącej obwód strojenia z obwodem aktywnym. W ustalonym stanie generacji rozchodzą się fale o amplitudach <math>U_i\,</math> i <math>U_r\,</math>. W tej wybranej płaszczyźnie określane są <math>\Gamma_a\,</math> współczynnik odbicia obwodu aktywnego i <math>\Gamma_c\,</math> współczynnik odbicia obwodu strojenia: | |||
'''Reflektancyjny warunek generacji''' jest zapisem oczywistego faktu, że jeden współczynnik jest odwrotnością drugiego: | |||
Oznaczymy moduły i argumenty obu współczynników odbicia: dla obwodu aktywnego <math>\Gamma_a=|\Gamma_a|e^{j\gamma_a}</math> i dla obwodu strojenia <math>\Gamma_c=|\Gamma_c|e^{j\gamma_c}</math> . Warunek generacji można zapisać dwoma równościami: warunkiem amplitudy, oraz warunkiem fazy. | |||
Współczynnik odbicia obwodu aktywnego <math>\Gamma_a=\Gamma_{a0}(U_0, I_0, \omega)S(|U_r|)</math> jest funkcją kilku zmiennych, podobnie jak admitancja <math>Y_a\,</math>. Natomiast współczynnik odbicia obwodu strojenia <math>\Gamma_S(\omega)\,</math> jest funkcją częstotliwości. Ilustracja warunku generacji na płaszczyźnie zespolonej wymaga wykreślenia zależności <math>\Gamma_S(\omega)\,</math> i odwrotności <math>1/{\Gamma_a}(P)\,</math>, co pokazano na rysunku b). | |||
Punkt przecięcia wskazuje stan ustalony generacji. Położenie tego punktu na linii <math>\Gamma_S(\omega)\,</math> wyznacza częstotliwość oscylacji, a na linii <math>1/{\Gamma_a}(P)\,</math> wyznacza moc oscylacji. | |||
Wersja z 13:33, 23 sie 2006

|
Materiał obu części Wykładu jest obszerny i zapoznaje on studiującego z wieloma nowymi zagadnieniami, technikami i z wielką liczbą nowych pojęć. |