PF Moduł 5: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 259: | Linia 259: | ||
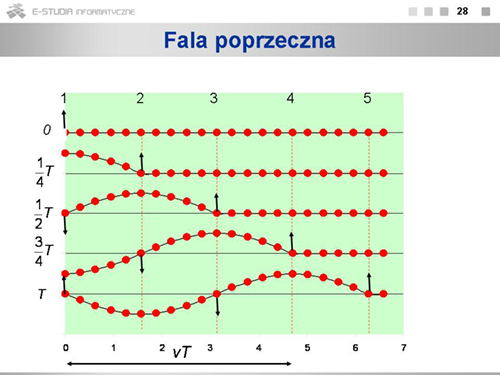
Rysunek pokazuje ruch cząsteczek podczas rozchodzenia się fali poprzecznej. Numerami <math>1, 2,...\</math> oznaczone są cząstki odległe od siebie o <math>\frac{1}{4} vT\,</math>, czyli odległość, jaką fala przebywa w czasie <math>\frac{1}{4}\,</math> okresu drgań. W chwili <math>t=0\,</math> fala biegnąca w prawo dochodzi do cząstki <math>1,</math>. Cząstka ta rozpoczyna ruch ku górze, pociągając za sobą kolejne cząstki. Po upływie <math>\frac{1}{4}\,</math> okresu cząstka 1 osiąga maksymalne wychylenie, a ruch ku górze rozpoczyna cząstka <math>2,</math>. Po następnej ćwiartce okresu cząstka 1 wraca do położenia równowagi i rozpoczyna ruch w dół, cząstka <math>2,</math> osiąga maksymalne wychylenie, a cząstka <math>3,</math> zaczyna przemieszczać się do góry. Po upływie pełnego okresu w chwili <math>t=T\,</math> pierwsza cząstka wraca do stanu, w jakim była w chwili <math>t=0\,</math>, a fala, przebywając drogę <math>vT\,</math>, dociera do cząstki <math>5,</math>. | Rysunek pokazuje ruch cząsteczek podczas rozchodzenia się fali poprzecznej. Numerami <math>1, 2,...\</math> oznaczone są cząstki odległe od siebie o <math>\frac{1}{4} vT\,</math>, czyli odległość, jaką fala przebywa w czasie <math>\frac{1}{4}\,</math> okresu drgań. W chwili <math>t=0\,</math> fala biegnąca w prawo dochodzi do cząstki <math>1,</math>. Cząstka ta rozpoczyna ruch ku górze, pociągając za sobą kolejne cząstki. Po upływie <math>\frac{1}{4}\,</math> okresu cząstka 1 osiąga maksymalne wychylenie, a ruch ku górze rozpoczyna cząstka <math>2,</math>. Po następnej ćwiartce okresu cząstka 1 wraca do położenia równowagi i rozpoczyna ruch w dół, cząstka <math>2,</math> osiąga maksymalne wychylenie, a cząstka <math>3,</math> zaczyna przemieszczać się do góry. Po upływie pełnego okresu w chwili <math>t=T\,</math> pierwsza cząstka wraca do stanu, w jakim była w chwili <math>t=0\,</math>, a fala, przebywając drogę <math>vT\,</math>, dociera do cząstki <math>5,</math>. | ||
|} | |||
---- | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="450px" valign="top"|[[Grafika:PF_M5_Slajd29.png]] | |||
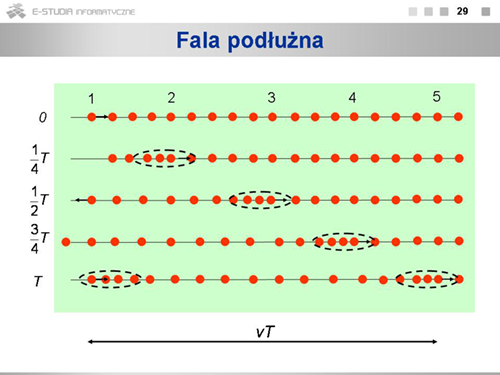
|valign="top"|Falą podłużną nazywamy falę, której kierunek rozchodzenia się jest równoległy do kierunku drgań cząstek. | |||
Rysunek pokazuje ruch cząstek podczas rozchodzenia się w ośrodku fali podłużnej. Widać, że rozchodzenie się fali podłużnej związane jest z powstawaniem w ośrodku postępujących po sobie zagęszczeń i rozrzedzeń cząstek. Zagęszczenia i rozrzedzenia przesuwają się w ośrodku z prędkością <math>v\,</math>. | |||
|} | |||
---- | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="450px" valign="top"|[[Grafika:PF_M5_Slajd30.png]] | |||
|valign="top"|Podczas rozchodzenia się fali w drganiach biorą udział nie tylko cząstki leżące na osi <math>x\,</math>, jak na poprzednich rysunkach, lecz układ cząstek znajdujących się w pewnej objętości. Zbiór punktów, do których fala dochodzi w danej chwili nazywamy czołem fali. Zbiór punktów drgających w tej samej fazie nazywamy powierzchnią falową. Przez każdy punkt biorący udział w ruchu falowym można przeprowadzić powierzchnię falową. Powierzchni falowych jest więc nieskończenie wiele, ale czoło fali jest tylko jedno. Spośród wszystkich możliwych kształtów powierzchni falowych wyróżniamy takie, które są płaszczyznami i powierzchniami kulistymi. Fale takie nazywamy odpowiednio falą płaską i falą kulistą. | |||
|} | |||
---- | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="450px" valign="top"|[[Grafika:PF_M5_Slajd31.png]] | |||
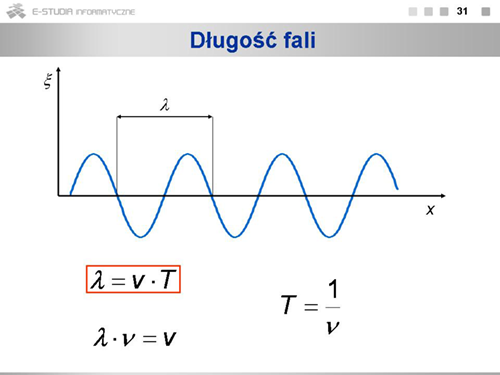
|valign="top"|Rysunek przedstawia wychylenia cząstek z położenia równowagi <math>\xi(x)\,</math> dla cząstek o różnych wartościach <math>x\,</math>. Zauważmy, że wykres ten może dotyczyć zarówno fali poprzecznej, jak i podłużnej. Długością fali nazywamy odległość, na jaką rozchodzi się fala w czasie równym okresowi drgań ośrodka. Można też powiedzieć, że długość fali to najmniejsza odległość między cząstkami drgającymi w jednakowej fazie. Długość fali związana jest okresem drgań prostym wzorem: <math>\lambda=v\cdot T\,</math> . | |||
|} | |||
---- | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="450px" valign="top"|[[Grafika:PF_M5_Slajd32.png]] | |||
|valign="top"|Równaniem fali nazywamy zależność wychylenia <math>\xi\,</math> drgającej cząstki od czasu <math>t\,</math> i od współrzędnych tej cząstki <math>(x, y, z)\,</math>: <math>\xi=\xi(x, y, z, t)\,</math> . Określimy to wyrażenie dla fali płaskiej biegnącej w kierunku osi <math>x\,</math>. Powierzchnie falowe są płaszczyznami prostopadłymi do osi <math>x\,</math>, więc wychylenie zależy tylko od <math>x\,</math> i <math>t\,</math>: <math>\xi=\xi(x, t)\,</math> . Drgania punktów leżących w płaszczyźnie <math>x=0\,</math> można opisać wzorem: <math>\xi(0, t)=a cos(\omega t +\varphi)\,</math> . Jak będą drgały punkty w płaszczyźnie odpowiadającej dowolnej wartości <math>x\,</math>? Drogę <math>x\,</math> fala przebędzie w czasie <math>\tau=x/v</math> . O taki czas będą opóźnione drgania w punkcie <math>x\,</math> w stosunku do <math>x=0\,</math>: | |||
<math>\xi(x, t)=a cos[\omega (t-\tau) +\varphi]=a cos \left[\omega\left(t-\frac{x}{v} \right) \right+\varphi]</math> | |||
|} | |||
---- | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="450px" valign="top"|[[Grafika:PF_M5_Slajd33.png]] | |||
|valign="top"|Argument funkcji cosinus nazywamy fazą. Z jaką prędkością przesuwa się dana wartość fazy? Wyrażenie: <math>\omega\left(t-\frac{x}{v} \right) +\varphi=const</math> wiąże wartości <math>x\,</math> i <math>t\,</math>, dla których faza ma daną wartość. Po zróżniczkowaniu tego wyrażenia otrzymujemy: <math>v=\frac<dx><dt></math> . Prędkość v nazywamy prędkością fazową, bo jest to prędkość przemieszczania się fazy. | |||
Wersja z 07:17, 21 sie 2006

|

|
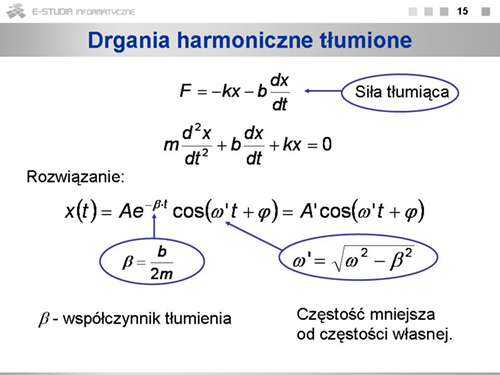
Sprawdźmy, czy nasze równanie będzie spełnione przez funkcję , gdzie , i są dowolnymi parametrami. Obliczamy pierwszą i drugą pochodną wychylenia po czasie i podstawiamy do równania. |

|
Okres i częstotliwość drgań
Okresem nazywamy czas jednego pełnego drgania. Po upływie okresu drgające ciało jest znów w takiej samej fazie. Okres powiązany jest z częstością wzorem: |

|
Prędkość i przyspieszenie
Prędkość i przyspieszenie w ruchu harmonicznym obliczamy jako pierwszą i drugą pochodną wychylenia po czasie. |

|
Energię kinetyczną w ruchu harmonicznym obliczamy, podstawiając do wzoru na energię kinetyczną prędkość w postaci . |
|
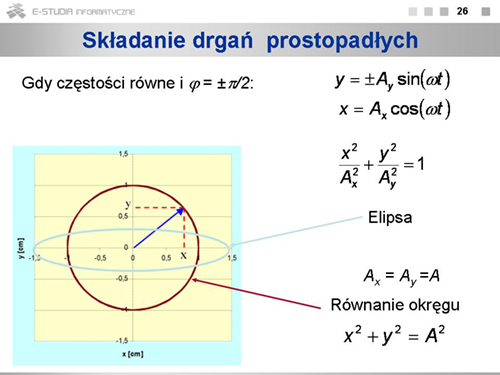
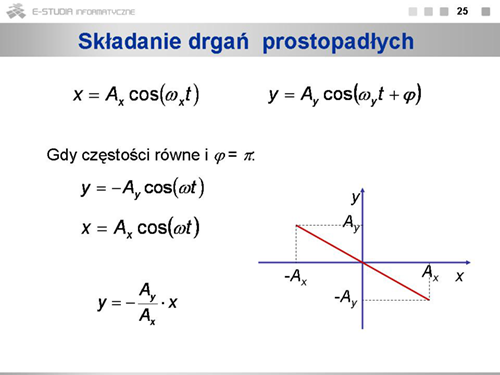
Jeśli częstości drgań są jednakowe i różnica faz wynosi , to ruch będzie ruchem harmonicznym wzdłuż prostej o równaniu . |