PF Moduł 5: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 247: | Linia 247: | ||
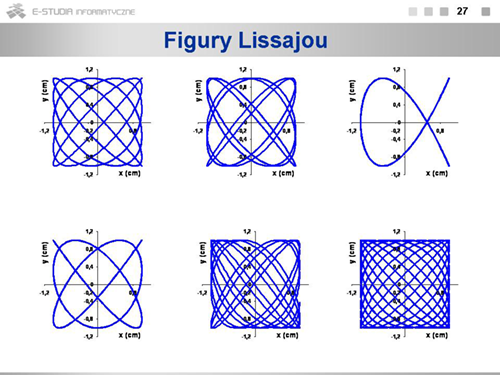
Stosunek liczby punktów stycznych do obu boków prostokąta wyznacza stosunek częstości obu ruchów składowych: <math>\omega_x/{\omega_y}\,</math> Rysunek pokazuje przykłady takich figur. | Stosunek liczby punktów stycznych do obu boków prostokąta wyznacza stosunek częstości obu ruchów składowych: <math>\omega_x/{\omega_y}\,</math> Rysunek pokazuje przykłady takich figur. | ||
|} | |||
---- | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="450px" valign="top"|[[Grafika:PF_M5_Slajd28.png]] | |||
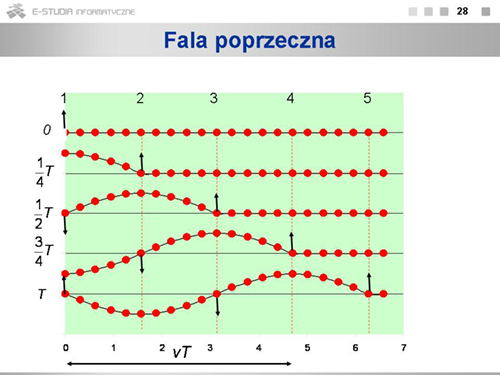
|valign="top"|'''Rozchodzenie się fal w ośrodku sprężystym''' | |||
Jeśli jakimś miejscu ośrodka sprężystego wywołamy drganie, to drgająca cząstka pociągnie za sobą kolejne cząstki i ruch drgający będzie się przenosić od cząstki do cząstki z pewną prędkością <math>v\,</math>. Takie rozchodzenie się drgań w ośrodku nazywamy falą. Należy podkreślić, że poszczególne cząstki ośrodka nie przemieszczają się, wykonują tylko drgania wokół swoich położeń równowagi. Jeśli drgania zachodzą w kierunku prostopadłym do kierunku rozchodzenia się fali, falę nazywamy falą poprzeczną. | |||
Rysunek pokazuje ruch cząsteczek podczas rozchodzenia się fali poprzecznej. Numerami <math>1, 2,...\</math> oznaczone są cząstki odległe od siebie o <math>\frac{1}{4} vT\,</math>, czyli odległość, jaką fala przebywa w czasie <math>\frac{1}{4}\,</math> okresu drgań. W chwili <math>t=0\,</math> fala biegnąca w prawo dochodzi do cząstki <math>1,</math>. Cząstka ta rozpoczyna ruch ku górze, pociągając za sobą kolejne cząstki. Po upływie <math>\frac{1}{4}\,</math> okresu cząstka 1 osiąga maksymalne wychylenie, a ruch ku górze rozpoczyna cząstka <math>2,</math>. Po następnej ćwiartce okresu cząstka 1 wraca do położenia równowagi i rozpoczyna ruch w dół, cząstka <math>2,</math> osiąga maksymalne wychylenie, a cząstka <math>3,</math> zaczyna przemieszczać się do góry. Po upływie pełnego okresu w chwili <math>t=T\,</math> pierwsza cząstka wraca do stanu, w jakim była w chwili <math>t=0\,</math>, a fala, przebywając drogę <math>vT\,</math>, dociera do cząstki <math>5,</math>. | |||
Wersja z 06:56, 21 sie 2006

|

|
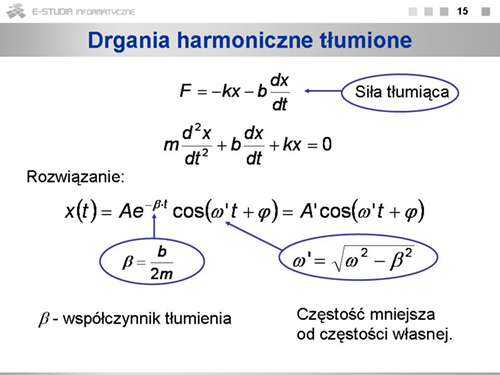
Sprawdźmy, czy nasze równanie będzie spełnione przez funkcję , gdzie , i są dowolnymi parametrami. Obliczamy pierwszą i drugą pochodną wychylenia po czasie i podstawiamy do równania. |

|
Okres i częstotliwość drgań
Okresem nazywamy czas jednego pełnego drgania. Po upływie okresu drgające ciało jest znów w takiej samej fazie. Okres powiązany jest z częstością wzorem: |

|
Prędkość i przyspieszenie
Prędkość i przyspieszenie w ruchu harmonicznym obliczamy jako pierwszą i drugą pochodną wychylenia po czasie. |

|
Energię kinetyczną w ruchu harmonicznym obliczamy, podstawiając do wzoru na energię kinetyczną prędkość w postaci . |
|
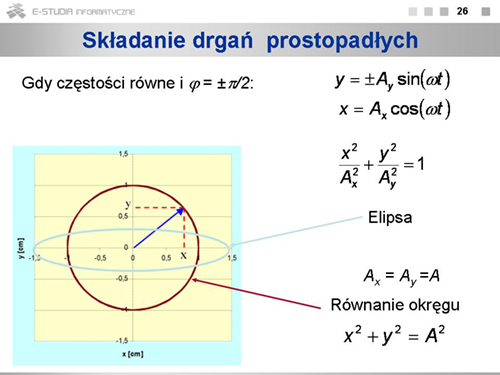
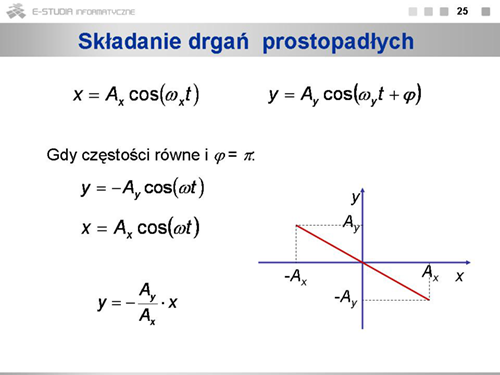
Jeśli częstości drgań są jednakowe i różnica faz wynosi , to ruch będzie ruchem harmonicznym wzdłuż prostej o równaniu . |