PF Moduł 5

---

Wstęp W życiu codziennym często spotykamy się z ruchami periodycznymi, gdy ciało porusza się tam i z powrotem, wracając co pewien czas do tego samego punktu. Może to być ruch huśtawki, drgania strun w instrumentach muzycznych, ruch ciężarka wiszącego na sprężynie, czy drgania szyb okiennych przy hałaśliwej ulicy. Ruch taki nazywamy ruchem okresowym, drgającym lub oscylacyjnym. Drgania dotyczą często periodycznych zmian innych wielkości niż położenie ciała, na przykład napięcia elektrycznego lub ciśnienia. Ruchy drgające można opisać, w sposób dokładny lub przybliżony, za pomocą wyrażeń zawierających funkcje sinus i cosinus. Funkcje te nazywamy funkcjami harmonicznymi, zaś opis taki nosi nazwę analizy harmonicznej. W przypadkach niektórych ruchów drgających, zwanych ruchami harmonicznymi, opis ten jest szczególnie prosty. Siły wywołujące te ruchy nazywamy siłami harmonicznymi. Ruchy sinusoidalne, czyli takie, które można opisać funkcjami sinus i cosinus, są najbardziej powszechną formą ruchu, dlatego są ważnym przedmiotem badań fizyki. Pamiętajmy, że ruchy harmoniczne są ruchami drgającymi, jednak nie wszystkie ruchy należące do klasy ruchów okresowych, drgających lub oscylacyjnych są ruchami harmonicznymi. Jeśli drga cząstka ośrodka sprężystego, drgania te przenoszą się na kolejne cząstki i w ośrodku rozchodzi się fala. W tym wykładzie omówione będą tylko fale w ośrodkach sprężystych, lecz pamiętajmy, że takimi samymi równaniami można opisać wiele zjawisk falowych: od fal rozchodzących się w strunie, poprzez fale dźwiękowe, aż do całej klasy fal elektromagnetycznych. Jak dowiemy się w dalszej części kursu, każda poruszająca się cząstka jest w istocie falą, tak więc równanie falowe spełnia fundamentalną rolę w opisie świata.

---

5.1. Równanie ruchu harmonicznego Ruch punktu materialnego nazywamy harmonicznym, jeśli porusza się on pod wpływem siły $F$ o wartości wprost proporcjonalnej do wychylenia z położenia równowagi $x$ i skierowanej przeciwnie do wychylenia. O zwrocie siły mówi znak minus we wzorze $F=-kx$, gdzie $k$ jest współczynnikiem proporcjonalności.

---

Jeśli siłę harmoniczną podstawimy do równania wyrażającego II zasadę dynamiki, otrzymamy równanie różniczkowe drugiego rzędu. Widzimy, że rozwiązaniem tego równania jest taka funkcja, której druga pochodna ma tą samą postać, co sama funkcja z przeciwnym znakiem (z dokładnością do stałej). Funkcjami takim są sinus i cosinus.

---

Sprawdźmy, czy nasze równanie będzie spełnione przez funkcję $x(t)=Acos(\omega \cdot t+\phi )$ , gdzie $A$, $\omega$ i $\phi$ są dowolnymi parametrami. Obliczamy pierwszą i drugą pochodną wychylenia $x$ po czasie $t$ i podstawiamy do równania.

---

Funkcja $x(t)=Acos(\omega \cdot t+\phi )$ spełnia równanie ruchu pod warunkiem, że stała $\omega$ spełnia związek: ${\omega }^2=k/m$. Stałą $\omega$ nazywamy częstością drgań własnych. Argument funkcji cosinus $(\omega \cdot t+\phi )$ to faza ruchu, $\phi$ stanowi fazę początkową w chwili $t=0$. Największe wychylenie z położenia równowagi nazywamy amplitudą drgań. Wynosi ona $A$, bowiem największa i najmniejsza wartość funkcji cosinus to 1 i -1.

---

Okres i częstotliwość drgań Okresem nazywamy czas jednego pełnego drgania. Po upływie okresu drgające ciało jest znów w takiej samej fazie. Okres powiązany jest z częstością wzorem: $T=2\pi /\omega$

---

Odwrotność okresu, czyli liczbę drgań w jednostce czasu nazywamy częstotliwością. Jednostką częstotliwości jest hertz $(1Hz=1s^{-1})$. Jeśli czas będziemy mierzyć od takiego momentu, że faza początkowa $\phi =-\pi /2$ , to ruch harmoniczny będzie opisany funkcją sinus. Jak widać wybór funkcji sinus czy cosinus jest w istocie wyborem fazy początkowej.

---

Prędkość i przyspieszenie Prędkość i przyspieszenie w ruchu harmonicznym obliczamy jako pierwszą i drugą pochodną wychylenia $x$ po czasie.

---

Wykres przedstawia zależność położenia, prędkości i przyspieszenia w ruchu harmonicznym od czasu. W momentach, gdy wychylenie z położenia równowagi jest maksymalne $(x=A)$, prędkość jest równa zeru, natomiast przyspieszenie ma wartość maksymalną, a znak przeciwny do wychylenia. Gdy drgające ciało znajduje się w położeniu równowagi $(x=0)$, przyspieszenie jest zerowe, a prędkość maksymalna.

---

Energia w ruchu harmonicznym Ciało wychylone z położenia równowagi, na które działa siła harmoniczna, ma pewną energię potencjalną. Energię tę można wyznaczyć, obliczając pracę jaką musimy wykonać, aby przesunąć ciało z położenia równowagi, $x=0$, do punktu o danym $x$. Zmiana energii potencjalnej $d{E}_p$ równa jest pracy, jaką wykonuje siła równoważąca siłę harmoniczną na drodze $dx$. Po obliczeniu całki w granicach od zera do $x$, otrzymujemy wzór na energię potencjalną ciała wychylonego z położenia równowagi o $x$: $E_p(x)=k{x}^2/2$ .

---

Energię kinetyczną w ruchu harmonicznym obliczamy, podstawiając do wzoru na energię kinetyczną $E_k=m{v}^2/2$ prędkość w postaci $v=-\omega Asin(\omega t+\varphi )$ .

---

Energia całkowita ciała poruszającego się ruchem harmonicznym to suma energii potencjalnej i kinetycznej. Wyciągamy wspólny czynnik przed nawias i zauważamy, że suma kwadratów sinusa i cosinusa równa jest 1. W ten sposób we wzorze na energię całkowitą znikło wyrażenie zależne od czasu. Oznacza to, że energia całkowita w ruchu harmonicznym nie zależy od czasu – jest w każdej chwili taka sama. Inaczej, energia całkowita jest zachowana. Zmieniają się natomiast energie kinetyczna i potencjalna, ale w ten sposób, że gdy jedna z nich rośnie, to druga maleje tak, że suma pozostaje stała. Wynik ten jest konsekwencją zasady zachowania energii mechanicznej pokazując, że siły harmoniczne są siłami zachowawczymi. Rzeczywiście, odchylenie ciała od położenia równowagi, to dostarczenie mu energii potencjalnej. Jeżeli potem nie ingerujemy w ruch ciała, to uzyskiwana w czasie ruchu do położenia równowagi energia kinetyczna jest równoważna traconej przez ciało energii potencjalnej. Po minięciu położenia równowagi sytuacja jest odwrotna - ciało traci energię kinetyczną, ale zyskuje potencjalną itd.

---

Pierwszy rysunek przedstawia zależność od położenia energii kinetycznej i potencjalnej oraz będącej ich sumą energii całkowitej. Widać, że energia kinetyczna jest największa w położeniu równowagi $(x=0)$, a energia potencjalna jest równa wtedy zeru. Gdy ciało jest maksymalnie wychylone $(x\pm A)$, energia kinetyczna jest równa zeru, a potencjalna maksymalna. Drugi rysunek pokazuje, jak zależy od czasu energia kinetyczna i potencjalna. Dla porównania przedstawiono również zależność od czasu położenia i prędkości. Zwróćmy uwagę, że zarówno energia kinetyczna, jak i potencjalna przyjmują tylko dodatnie wartości, a okres ich zmian jest dwa razy mniejszy niż okres zmian położenia i prędkości.

---

Drgania harmoniczne tłumione Rozważaliśmy dotąd wyidealizowany ruch harmoniczny, w którym nie występowały żadne siły oporu. Nasze doświadczenie życiowe wskazuje jednak, że każde drganie swobodne z czasem zanika, jego amplituda maleje i końcu ruch ustaje. Zanikanie drgań powodują siły oporu powietrza lub innych oporów występujących w układzie drgającym. Opory te są zwykle tym większe, im większa jest prędkość ciała. Czujemy to wyraźnie po wysunięciu ręki przez okno jadącego samochodu lub pociągu. Dla niewielkich prędkości siła oporu jest wprost proporcjonalna do prędkości. Równanie ruchu z uwzględnieniem siły oporu $F_o=-b\frac{dx}{dt}$ jest trudniejsze do rozwiązanie, dlatego podajemy tu końcową postać.

---

Zauważmy, że rozwiązanie dla drgań tłumionych ma postać bardzo podobną do rozwiązania opisującego drgania swobodne. Istotne są dwie różnice. Po pierwsze amplituda maleje wykładniczo z czasem. Po drugie częstość drgań tłumionych jest mniejsza niż drgań swobodnych, a więc tłumienie wydłuża okres.

---

Aby wyrażenie na okres miało sens, wyrażenie pod pierwiastkiem musi być większe od zera. Oznacza to, że aby zachodziły drgania, współczynnik tłumienia nie może być zbyt wielki. A co dzieje się, kiedy współczynnik tłumienia nie spełnia tego warunku? Wtedy tłumienie jest tak duże, że w ogóle nie dochodzi do drgań. Układ wraca do stanu równowagi w sposób wykładniczy.

---

Na ilustracji pokazane są wychylenia z położenia równowagi dla drgań swobodnych i tłumionych – górny wykres dla niezbyt dużej wartości współczynnika tłumienia, dolny dla współczynnika tłumienia tak dużego, że nie dochodzi do drgań.

---

Drgania harmoniczne wymuszone Dobrze wiemy, że aby długo huśtać się na huśtawce tak, jak dama na tym pięknym obrazie, potrzebny jest ktoś, kto będzie huśtawkę popychał w odpowiednich momentach. W ogólności siłę podtrzymującą drganie, zwaną też siłą wymuszającą, przedstawiamy jako siłę zależną sinusoidalnie od czasu. Na przykład może ona mieć postać: $F_w=F_0(co{s}_w\cdot t)$ . Równanie ruchu uwzględnia zarówno siłę wymuszającą, jak i tłumiącą drgania. Zwróćmy uwagę, że częstość siły wymuszającej ${\omega }_w$ jest w ogólnym przypadku inna niż częstość drgań własnych $\omega$ .

---

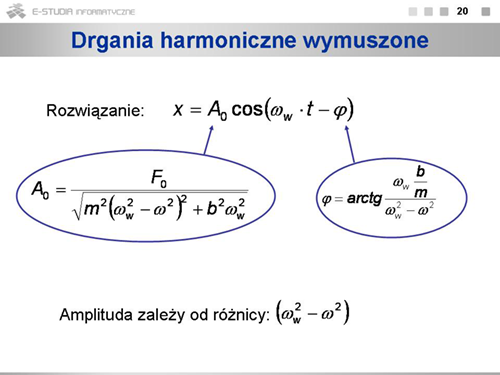
Rozwiązanie równania dla drgań wymuszonych ma podobną postać, co rozwiązanie dla drgań swobodnych. Należy zauważyć, że: Układ drga z częstością siły wymuszającej i jest ruchem nie tłumionym (amplituda nie maleje z upływem czasu). Amplituda drgań zależy zarówno od współczynnika tłumienia, jak i od różnicy pomiędzy częstością drgań własnych układu i częstością siły wymuszającej.

---

Analizując wzór na amplitudę drgań wymuszonych, widzimy, że można dobrać taką częstość siły wymuszającej, aby amplituda była maksymalna. Taki stan nazywamy rezonansem. Kiedy brak jest tłumienia $(b=0)$, a częstość rezonansowa równa jest częstości drgań własnych układu $({\omega }_w=\omega )$ , amplituda dąży do nieskończoności! Drgania stają się niezwykle gwałtowne. Dla wartości współczynników tłumienia różnych od zera amplituda osiąga największą wartość (czyli występuje rezonans) dla częstości określonych wzorem: ${\omega }_w=\sqrt{{\omega }^2-b^2/2m^2}$ , a więc mniejszych od częstości drgań własnych. Rysunek przedstawia kilka krzywych rezonansowych, czyli zależności amplitudy drgań od częstości siły wymuszającej dla kilku wartości współczynników tłumienia $\beta$ . Widać, że im większy współczynnik tłumienia, tym niższą wartość osiąga amplituda i tym bardziej częstość rezonansowa różni się od częstości drgań własnych, która tu wynosi $1s^{-1}$ .

---

Składanie drgań równoległych Jaki będzie wynik nałożenia się dwóch drgań harmonicznych o kierunkach równoległych, ale różnych częstościach, amplitudach i fazach? Wychylenie wypadkowe będzie sumą obu wychyleń. Intuicyjnie przewidujemy, że w chwili, gdy oba wychylenia są w tym samym kierunku - otrzymamy wzmocnienie, kiedy w przeciwnym - osłabienie sumarycznego wychylenia, $x$. Szczególnie ciekawy jest przypadek, kiedy obie częstości mają zbliżone wartości. Dla uproszczenia przyjmiemy, że amplitudy i fazy są takie same, a różnica ich częstości $\mathrm{\Delta }\omega$ jest niewielka. Po wykonaniu przekształceń trygonometrycznych otrzymujemy wzór przestawiający drganie harmoniczne, ale z amplitudą, która zmienia się periodycznie z częstością znacznie mniejszą od $\omega$ . Zjawisko to nazywamy dudnieniem.

---

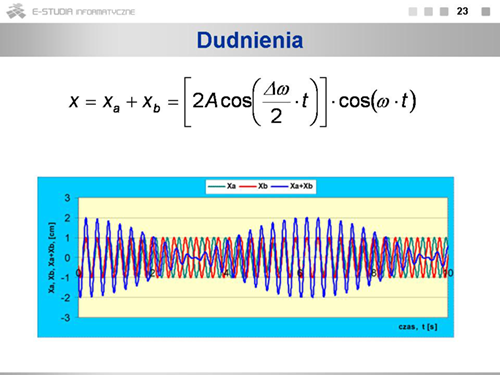
Wykres przedstawia zależność wychyleń drgań składowych $x_a$ i $x_b$ oraz ich sumy $x_a+x_b$ . Amplitudy drgań składowych są jednakowe i mają wartość 1 cm, natomiast amplituda drgań wypadkowych wolno oscyluje od zera do wartości 2 cm.

---

Składanie drgań prostopadłych Kiedy drgania punktu materialnego odbywają się równocześnie w dwóch prostopadłych do siebie kierunkach, na przykład wzdłuż osi $x$ i $y$ prostokątnego układu współrzędnych, to wypadkowy ruch tego punktu na płaszczyźnie można opisać z pomocą równań: $x=A_{x}cos({\omega }_{x}t)$ oraz $y=A_{y}cos({\omega }_{y}t+\phi )$ . Jeśli częstości drgań są jednakowe i różnica faz wynosi zero, to ruch wypadkowy będzie odbywał się wzdłuż prostej o równaniu $y=(A_y/A_x)\cdot x$ . Będzie to również drgania harmoniczne.