PF Moduł 16: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 341: | Linia 341: | ||
: <math>\nu'=\frac{(n+n_0)}{t}=\frac{\frac{vt}{\lambda}+\frac{v_0 t}{\lambda}}{t}=\frac{v+v_0}{\lambda}</math> | : <math>\nu'=\frac{(n+n_0)}{t}=\frac{\frac{vt}{\lambda}+\frac{v_0 t}{\lambda}}{t}=\frac{v+v_0}{\lambda}</math> | ||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="450px" valign="top"|[[Grafika:PF_M16_Slajd29.png]] | |||
|valign="top"|Ponieważ <math>\lambda=v/{\nu}</math> otrzymujemy: | |||
: <math>\nu'=\frac{\nu}{v}(v+v_0)=\nu\left(1+\frac{v_0}{v} \right)</math> | |||
a więc częstotliwość dźwięku odbierana przez obserwatora zbliżającego się do nieruchomego źródła, <math>\nu'\,</math>, jest większa od częstotliwości wysyłanej przez źródło, <math>\nu\,</math>. Odbierany dźwięk jest wyższy. | |||
Kiedy oddalamy się od nieruchomego źródła dźwięku to zmniejsza się liczba fal docierających do nas w danym czasie i ton słyszanego dźwięku jest niższy. Rozumując jak wyżej, mamy bowiem: | |||
: <math>\nu'=\nu \left(1-\frac{v_0}{v} \right)</math> | |||
a więc częstotliwość dźwięku odbieranego jest mniejsza od częstotliwości dźwięku wysyłanego. | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="450px" valign="top"|[[Grafika:PF_M16_Slajd30.png]] | |||
|valign="top"|Kiedy my się nie poruszamy, ale porusza się w naszym kierunku źródło dźwięku (na przykład zbliżający się samochód), to obrazowo możemy powiedzieć, że źródło (samochód) stara się dogonić uciekającą falę. W czasie jednego okresu fala przesunie się o odcinek , ale źródło przesunie się o odcinek , gdzie vz jest prędkością źródła. Długość fali będzie więc zmniejszona o odcinek jaki przebywa źródło w czasie jednego okresu: | |||
Wersja z 02:30, 18 sie 2006

|
|
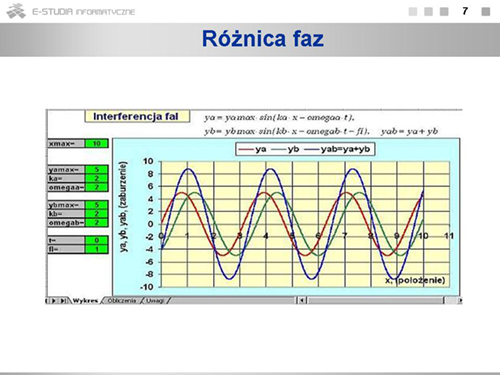
Kiedy inne parametry fal (na przykład częstość, amplituda) będą się różnić, fala wypadkowa nie musi być falą sinusoidalną. Możesz to sprawdzić sam, korzystając z załączonej ilustracji interaktywnej. |