PF Moduł 16: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 312: | Linia 312: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="450px" valign="top"|[[Grafika:PF_M16_Slajd27.png]] | |width="450px" valign="top"|[[Grafika:PF_M16_Slajd27.png]] | ||
|valign="top"|Efekty dyfrakcyjne możemy obserwować nie tylko dla światła widzialnego i dla fal przechodzących przez szczeliny. Ważną i wartościową z punktu widzenia badania struktur krystalicznych jest dyfrakcja odbiciowa wiązek promieni Roentgena na kryształach. Zjawisko dyfrakcji zachodzi na zbudowanej z atomów sieci krystalicznej i polega na nałożeniu się fal odbitych od płaszczyzn utworzonych przez atomy. Kryształ stanowi rodzaj trójwymiarowej siatki dyfrakcyjnej dla promieniowania o długościach fal porównywalnych z odległościami międzyatomowymi w krysztale. | |valign="top"|'''Prawo Bragga''' | ||
Efekty dyfrakcyjne możemy obserwować nie tylko dla światła widzialnego i dla fal przechodzących przez szczeliny. Ważną i wartościową z punktu widzenia badania struktur krystalicznych jest dyfrakcja odbiciowa wiązek promieni Roentgena na kryształach. Zjawisko dyfrakcji zachodzi na zbudowanej z atomów sieci krystalicznej i polega na nałożeniu się fal odbitych od płaszczyzn utworzonych przez atomy. Kryształ stanowi rodzaj trójwymiarowej siatki dyfrakcyjnej dla promieniowania o długościach fal porównywalnych z odległościami międzyatomowymi w krysztale. | |||
Przykład struktury sieci, przedstawiony w dwóch wymiarach, pokazuje rysunek. Kolorem czerwonym zaznaczone są węzły sieci, na których zachodzi zjawisko dyfrakcji. Odległość pomiędzy płaszczyznami poziomymi wynosi <math>d\,</math>. Kąt między płaszczyzną kryształu a promieniami padającymi równy jest <math>\theta\,</math>. Padające na kolejne płaszczyzny fale płaskie ulegają odbiciu i jeśli różnica dróg optycznych fal odbitych od poszczególnych warstw równa jest całkowitej wielokrotności długości fali padającej, to wypadkowa fala odbita ma maksymalną amplitudę. Warunek powstawania maksimów dyfrakcyjnych zwany jest prawem Bragga i wynika bezpośrednio z zależności geometrycznych widocznych na rysunku. Aby po odbiciu uformowane zostało czoło zgodnych w fazie fal musi być spełniony warunek <math>2d sin\theta=n\lambda</math> , gdzie <math>n=1, 2, 3,...\,</math> | Przykład struktury sieci, przedstawiony w dwóch wymiarach, pokazuje rysunek. Kolorem czerwonym zaznaczone są węzły sieci, na których zachodzi zjawisko dyfrakcji. Odległość pomiędzy płaszczyznami poziomymi wynosi <math>d\,</math>. Kąt między płaszczyzną kryształu a promieniami padającymi równy jest <math>\theta\,</math>. Padające na kolejne płaszczyzny fale płaskie ulegają odbiciu i jeśli różnica dróg optycznych fal odbitych od poszczególnych warstw równa jest całkowitej wielokrotności długości fali padającej, to wypadkowa fala odbita ma maksymalną amplitudę. Warunek powstawania maksimów dyfrakcyjnych zwany jest prawem Bragga i wynika bezpośrednio z zależności geometrycznych widocznych na rysunku. Aby po odbiciu uformowane zostało czoło zgodnych w fazie fal musi być spełniony warunek <math>2d sin\theta=n\lambda</math> , gdzie <math>n=1, 2, 3,...\,</math> | ||
Prawo Bragga znajduje zastosowanie do badania struktury sieci krystalicznej, na przykład określania odległości międzypłaszczyznowych. Z drugiej strony, umożliwia także analizę składu widmowego promieniowania Roentgena, stanowiąc element metod spektroskopii rentgenowskiej. Stosując kryształy o znanych parametrach sieci krystalicznej, można określić długość padającej fali, stosując promieniowanie o znanej długości można określić odległości pomiędzy płaszczyznami struktury krystalicznej. Z kolei, jeśli na określony kryształ rzucimy wiązkę promieniowania o różnych długościach fali (niemonochromatycznego), to w wyniku odbicia braggowskiego możemy otrzymać promieniowanie monochromatyczne o długościach fali spełniających prawo Bragga. | |||
Wersja z 02:02, 18 sie 2006

|
|
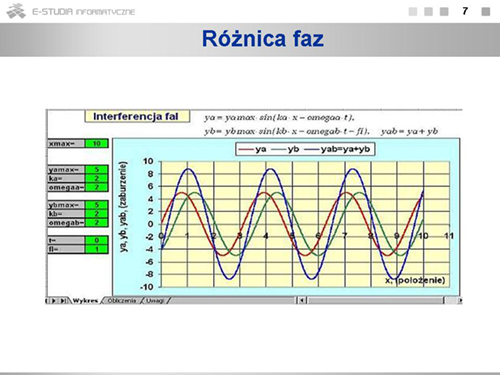
Kiedy inne parametry fal (na przykład częstość, amplituda) będą się różnić, fala wypadkowa nie musi być falą sinusoidalną. Możesz to sprawdzić sam, korzystając z załączonej ilustracji interaktywnej. |