PF Moduł 16: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 233: | Linia 233: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="450px" valign="top"|[[Grafika: | |width="450px" valign="top"|[[Grafika:PF_M16_Slajd21.png]] | ||
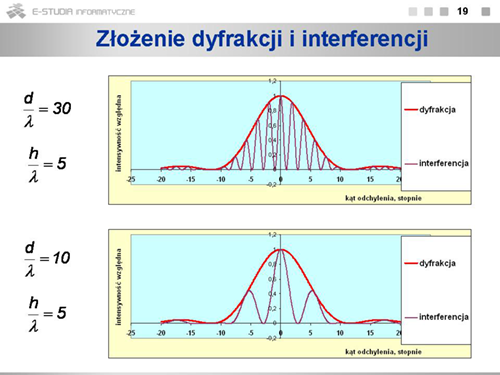
|valign="top"|Siatką dyfrakcyjną nazywamy układ wielu szczelin. Charakteryzuje ją wielkość zwana stałą siatki <math>d\,</math>, która równa jest odległości pomiędzy dwiema sąsiednimi szczelinami, szerokość szczeliny <math>h\,</math> oraz liczba szczelin <math>N\,</math>. Oczekujemy, że w przypadku siatki dyfrakcyjnej efekt interferencyjny będzie silniejszy, bo sumować się będą składniki pochodzące od każdej pary sąsiednich szczelin. Wystąpią też efekty dodatkowe związane z interferencją pomiędzy innymi kombinacjami dwóch szczelin w siatce. Warunek wzmocnienia dla par sąsiednich szczelin będzie taki sam jak dla układu dwóch szczelin, czyli kąt odchylenia określony będzie stosunkiem długości fali padającej do stałej siatki. Podobnie jak w przypadku dwóch szczelin o określonych szerokościach wystąpią też efekty dyfrakcyjne zależne od szerokości samych szczelin <math>h\,</math>. Zapiszmy więc warunek wzmocnienia w postaci: <math>sin\theta=n\frac{\lambda}{d}</math> , gdzie <math>n=1, 2, 3,...\,</math> | |valign="top"|Siatką dyfrakcyjną nazywamy układ wielu szczelin. Charakteryzuje ją wielkość zwana stałą siatki <math>d\,</math>, która równa jest odległości pomiędzy dwiema sąsiednimi szczelinami, szerokość szczeliny <math>h\,</math> oraz liczba szczelin <math>N\,</math>. Oczekujemy, że w przypadku siatki dyfrakcyjnej efekt interferencyjny będzie silniejszy, bo sumować się będą składniki pochodzące od każdej pary sąsiednich szczelin. Wystąpią też efekty dodatkowe związane z interferencją pomiędzy innymi kombinacjami dwóch szczelin w siatce. Warunek wzmocnienia dla par sąsiednich szczelin będzie taki sam jak dla układu dwóch szczelin, czyli kąt odchylenia określony będzie stosunkiem długości fali padającej do stałej siatki. Podobnie jak w przypadku dwóch szczelin o określonych szerokościach wystąpią też efekty dyfrakcyjne zależne od szerokości samych szczelin <math>h\,</math>. Zapiszmy więc warunek wzmocnienia w postaci: <math>sin\theta=n\frac{\lambda}{d}</math> , gdzie <math>n=1, 2, 3,...\,</math> | ||
Wielkość <math>n\,</math> nazywamy rzędem widma. | Wielkość <math>n\,</math> nazywamy rzędem widma. | ||
Wersja z 20:43, 17 sie 2006

|
|
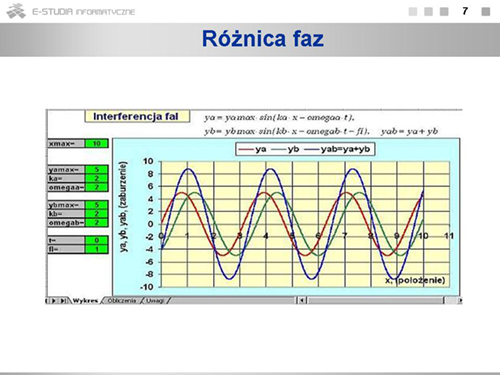
Kiedy inne parametry fal (na przykład częstość, amplituda) będą się różnić, fala wypadkowa nie musi być falą sinusoidalną. Możesz to sprawdzić sam, korzystając z załączonej ilustracji interaktywnej. |