PF Moduł 16: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 211: | Linia 211: | ||
Jest to końcowy wzór zależny wyłącznie od wielkości mierzalnych. Indeksami "i" i "d" oznaczyliśmy kąty odpowiadające interferencji i dyfrakcji. Symbolem d oznaczona jest odległość pomiędzy szczelinami, a symbolem h, szerokość każdej ze szczelin. <math>I_m\,</math> jest maksymalną intensywnością odpowiadającą promieniom biegnącym na wprost. | Jest to końcowy wzór zależny wyłącznie od wielkości mierzalnych. Indeksami "i" i "d" oznaczyliśmy kąty odpowiadające interferencji i dyfrakcji. Symbolem d oznaczona jest odległość pomiędzy szczelinami, a symbolem h, szerokość każdej ze szczelin. <math>I_m\,</math> jest maksymalną intensywnością odpowiadającą promieniom biegnącym na wprost. | ||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="450px" valign="top"|[[Grafika:PF_M16_Slajd19.png]] | |||
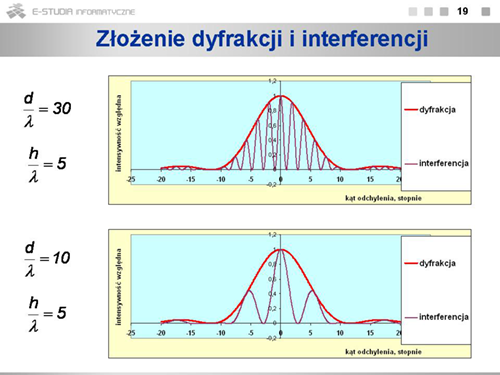
|valign="top"|Obraz interferencyjno - dyfrakcyjny określony powyższym wzorem pokazany jest na rysunku. Widzimy tu szereg maksimów interferencyjnych (fioletowa linia), których intensywność określona jest przez efekty dyfrakcyjne (czerwona linia). Dolny wykres odpowiada trzy razy mniejszej odległości między szczelinami d niż górny. Zmniejszenie odległości wpłynęło na poszerzenie linii. | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="450px" valign="top"|[[Grafika:PF_M16_Slajd20.png]] | |||
|valign="top"|Szerokość szczelin <math>h\,</math> wpływa natomiast na zależność intensywności linii od kąta odchylenia <math>\theta\,</math>. Dla szerokich szczelin intensywność szybko maleje wraz z kątem <math>\theta\,</math>, dla szczelin wąskich możemy obserwować stosunkowo silne linie przy dużych kątach odchylenia. | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="450px" valign="top"|[[Grafika:PF_M16_Slajd20.png]] | |||
|valign="top"|Siatką dyfrakcyjną nazywamy układ wielu szczelin. Charakteryzuje ją wielkość zwana stałą siatki <math>d\,</math>, która równa jest odległości pomiędzy dwiema sąsiednimi szczelinami, szerokość szczeliny <math>h\,</math> oraz liczba szczelin <math>N\,</math>. Oczekujemy, że w przypadku siatki dyfrakcyjnej efekt interferencyjny będzie silniejszy, bo sumować się będą składniki pochodzące od każdej pary sąsiednich szczelin. Wystąpią też efekty dodatkowe związane z interferencją pomiędzy innymi kombinacjami dwóch szczelin w siatce. Warunek wzmocnienia dla par sąsiednich szczelin będzie taki sam jak dla układu dwóch szczelin, czyli kąt odchylenia określony będzie stosunkiem długości fali padającej do stałej siatki. Podobnie jak w przypadku dwóch szczelin o określonych szerokościach wystąpią też efekty dyfrakcyjne zależne od szerokości samych szczelin <math>h\,</math>. Zapiszmy więc warunek wzmocnienia w postaci: <math>sin\theta=n\frac{\lambda}{d}</math> , gdzie <math>n=1, 2, 3,...\,</math> | |||
Wielkość <math>n\,</math> nazywamy rzędem widma. | |||
Wersja z 20:17, 17 sie 2006

|
|
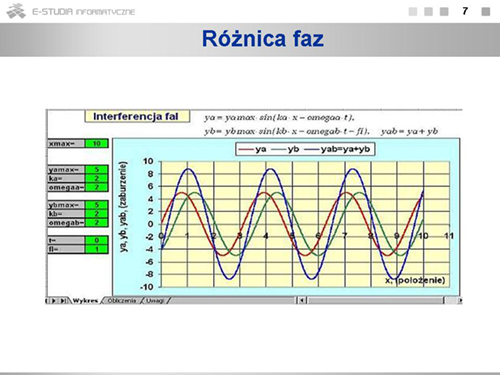
Kiedy inne parametry fal (na przykład częstość, amplituda) będą się różnić, fala wypadkowa nie musi być falą sinusoidalną. Możesz to sprawdzić sam, korzystając z załączonej ilustracji interaktywnej. |