PF Moduł 16: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 166: | Linia 166: | ||
W ten sposób różnica faz <math>\varphi\,</math> określona została przez mierzalne wielkości: szerokość szczeliny <math>h\,</math>, długość fali <math>\lambda\,</math> i kąt obserwacji <math>\theta\,</math>. Podstawiając wyznaczoną wypadkową różnicę faz do wzoru <math>E_{\theta}=E_0 \frac{sin\alpha}{\alpha}</math> , otrzymujemy wyrażenie na amplitudę fali wypadkowej. Intensywność obrazu dyfrakcyjnego proporcjonalna jest do kwadratu amplitudy. Zapiszmy więc kompletny wzór na rozkład intensywności obrazu dyfrakcyjnego zależny jedynie od mierzalnych wielkości, czyli umożliwiający weryfikację doświadczalną. Przez <math>I_{wzgl}\,</math> oznaczamy względną intensywność określoną jako stosunek intensywności dla danego kąta do intensywności maksymalnej, czyli dla kąta <math>\theta\,</math> równego zeru. | W ten sposób różnica faz <math>\varphi\,</math> określona została przez mierzalne wielkości: szerokość szczeliny <math>h\,</math>, długość fali <math>\lambda\,</math> i kąt obserwacji <math>\theta\,</math>. Podstawiając wyznaczoną wypadkową różnicę faz do wzoru <math>E_{\theta}=E_0 \frac{sin\alpha}{\alpha}</math> , otrzymujemy wyrażenie na amplitudę fali wypadkowej. Intensywność obrazu dyfrakcyjnego proporcjonalna jest do kwadratu amplitudy. Zapiszmy więc kompletny wzór na rozkład intensywności obrazu dyfrakcyjnego zależny jedynie od mierzalnych wielkości, czyli umożliwiający weryfikację doświadczalną. Przez <math>I_{wzgl}\,</math> oznaczamy względną intensywność określoną jako stosunek intensywności dla danego kąta do intensywności maksymalnej, czyli dla kąta <math>\theta\,</math> równego zeru. | ||
<math>I_{\theta}=I_0 \left(\frac{sin\alpha}{\alpha} \right)^2</math> , lub <math>I_{wzgl}=\frac{I_{\theta}}{I_0} =\left(\frac{sin\alpha}{\alpha} \right)^2</math> , gdzie <math>\alpha=\pi \left(\frac{h}{\lambda} \right)sin\theta</math> | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="450px" valign="top"|[[Grafika:PF_M16_Slajd16.png]] | |||
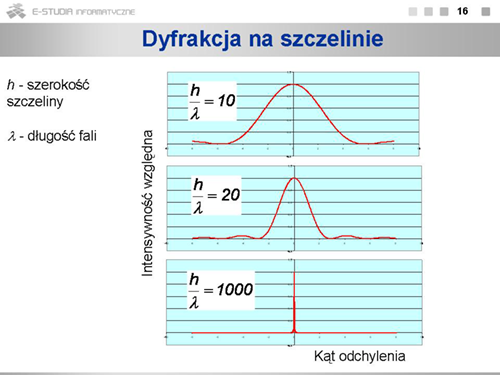
|valign="top"|Warto zobaczyć, jak zmiana intensywności zależy od szerokości szczeliny i długości fali. Z postaci wzoru na <math>I_{wzgl}\,</math> widać, że zależy nie tyle od samych tych wartości, ale od ich stosunku <math>h/{\lambda}\,</math> . Szerokość głównego maksimum dyfrakcyjnego jest tym większa, im węższa jest szczelina. Gdy szerokość szczeliny jest dużo większa od długości fali (dolny wykres) zjawiska dyfrakcji, czyli ugięcia na szczelinie, praktycznie nie obserwujemy. | |||
Wersja z 19:49, 17 sie 2006

|
|
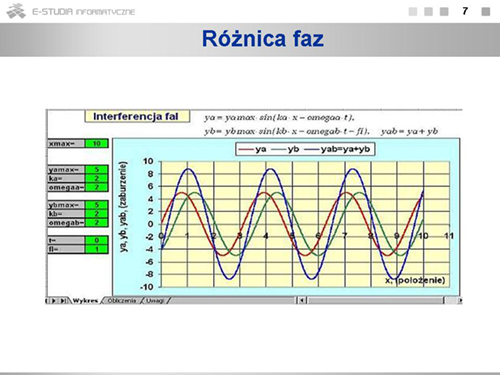
Kiedy inne parametry fal (na przykład częstość, amplituda) będą się różnić, fala wypadkowa nie musi być falą sinusoidalną. Możesz to sprawdzić sam, korzystając z załączonej ilustracji interaktywnej. |