PF Moduł 16: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 153: | Linia 153: | ||
|valign="top"|W naszym przypadku fali przechodzącej przez szczelinę, sumaryczna amplituda i sumaryczna faza będzie złożeniem n składowych i zależeć będzie, zgodnie ze wzorem <math>\Delta \varphi=\frac{2\pi}{\lambda}\Delta h sin\theta</math> od kąta <math>\theta\,</math> określającego położenie danego punktu na ekranie względem szczeliny. | |valign="top"|W naszym przypadku fali przechodzącej przez szczelinę, sumaryczna amplituda i sumaryczna faza będzie złożeniem n składowych i zależeć będzie, zgodnie ze wzorem <math>\Delta \varphi=\frac{2\pi}{\lambda}\Delta h sin\theta</math> od kąta <math>\theta\,</math> określającego położenie danego punktu na ekranie względem szczeliny. | ||
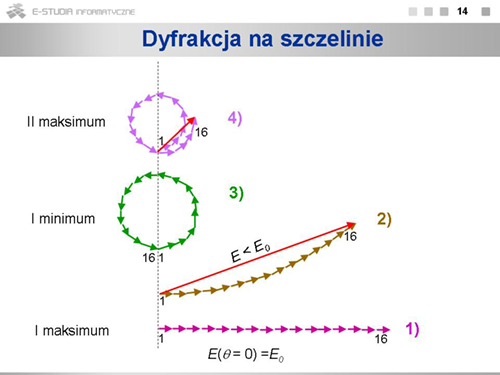
Jeśli kąt ten jest równy zeru, czyli punkt obserwacji leży na wprost szczeliny, to i <math>\Delta \varphi</math> będzie równe zeru i sumaryczna amplituda będzie algebraiczną sumą <math>n\,</math> jednakowych składników. Jeśli kąt <math>\theta\,</math> będzie inny, musimy sumować <math>n\,</math> fal składowych zgodnie z metodą strzałek fazowych. Ilustruje to rysunek, gdzie <math>n=16\,</math>. Przypadek 1) odpowiada sytuacji, gdy <math>\theta=0</math>, a więc i różnica faz <math>\Delta \varphi=0</math>. Sumaryczna amplituda jest tu maksymalna, oznaczyliśmy ją <math>E_0\,</math>. Kolejne przypadki 2), 3) i 4) odpowiadają wzrastającej wartości kąta obserwacji <math>\theta\,</math>. Przypadek 2) ilustruje sytuację, gdy <math>\theta\,</math> nieco większe od zera. Suma algebraiczna wszystkich 16 składników (długość łuku) jest taka sama, jak poprzednio, równa <math>E_0\,</math>, ale wypadkowa amplituda (wartość sumy wektorowej) jest mniejsza od <math>E_0\,</math>. W przypadku 3) sumaryczna amplituda wynosi zero, czyli będzie to pierwsze minimum. Przy dalszym wzroście kąta <math>\theta\,</math> amplituda znów będzie różna od zera, ale jej wartość stanie się o wiele mniejsza. Liczba pasków, na które podzieliliśmy w myśli szczelinę może być dowolna. Im będzie większa, tym węższe będą paski, ale końcowe przesunięcie fazowe i zmiana amplitudy będą, dla danej długości fali, określone tylko wartością kąta odchylenia <math>\theta\,</math>. (Pomocniczy wskaźnik n przestaje więc być istotny i dalej potrzebny.) Związek pomiędzy wartością kąta <math>\theta\,</math>, a amplitudą wypadkowej fali możemy znaleźć rozpatrując zależności geometryczne zilustrowane na rysunku. | Jeśli kąt ten jest równy zeru, czyli punkt obserwacji leży na wprost szczeliny, to i <math>\Delta \varphi</math> będzie równe zeru i sumaryczna amplituda będzie algebraiczną sumą <math>n\,</math> jednakowych składników. Jeśli kąt <math>\theta\,</math> będzie inny, musimy sumować <math>n\,</math> fal składowych zgodnie z metodą strzałek fazowych. Ilustruje to rysunek, gdzie <math>n=16\,</math>. Przypadek 1) odpowiada sytuacji, gdy <math>\theta=0</math>, a więc i różnica faz <math>\Delta \varphi=0</math>. Sumaryczna amplituda jest tu maksymalna, oznaczyliśmy ją <math>E_0\,</math>. Kolejne przypadki 2), 3) i 4) odpowiadają wzrastającej wartości kąta obserwacji <math>\theta\,</math>. Przypadek 2) ilustruje sytuację, gdy <math>\theta\,</math> nieco większe od zera. Suma algebraiczna wszystkich 16 składników (długość łuku) jest taka sama, jak poprzednio, równa <math>E_0\,</math>, ale wypadkowa amplituda (wartość sumy wektorowej) jest mniejsza od <math>E_0\,</math>. W przypadku 3) sumaryczna amplituda wynosi zero, czyli będzie to pierwsze minimum. Przy dalszym wzroście kąta <math>\theta\,</math> amplituda znów będzie różna od zera, ale jej wartość stanie się o wiele mniejsza. Liczba pasków, na które podzieliliśmy w myśli szczelinę może być dowolna. Im będzie większa, tym węższe będą paski, ale końcowe przesunięcie fazowe i zmiana amplitudy będą, dla danej długości fali, określone tylko wartością kąta odchylenia <math>\theta\,</math>. (Pomocniczy wskaźnik <math>n\,</math> przestaje więc być istotny i dalej potrzebny.) Związek pomiędzy wartością kąta <math>\theta\,</math>, a amplitudą wypadkowej fali możemy znaleźć rozpatrując zależności geometryczne zilustrowane na rysunku. | ||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="450px" valign="top"|[[Grafika:PF_M16_Slajd15.png]] | |||
|valign="top"|Kiedy liczba pasków będzie zmierzać do nieskończoności, a ich szerokość do zera, to łuk strzałek fazowych będzie można przybliżyć łukiem okręgu. Długość łuku jest równa <math>E_0\,</math>, a kąt <math>\varphi\,</math> pomiędzy stycznymi do łuku na obu jego końcach równy jest różnicy faz pomiędzy promieniami biegnącymi z obu krańców szczeliny. Kąt ten, mierzony w radianach, równy jest z definicji stosunkowi długości łuku, czyli <math>E_0\,</math>, do promienia <math>R\,</math> to znaczy <math>\varphi=E_0/R\,</math>. Z kolei, jak widać na rysunku, wypadkowa amplituda fali obserwowanej pod kątem <math>\theta\,</math> wynosi <math>E_{\theta}=2Rsin\alpha</math> , zaś <math>\alpha=\varphi/2</math> . Wynika z tego, że <math>E_{\theta}=E_0 \frac{sin\alpha}{\alpha}</math>. | |||
Wypadkowa różnica faz odpowiada promieniom biegnącym z dwóch krańców szczeliny i określona jest tak samo, jak różnica faz dla dwóch sąsiednich pasków, jeśli szerokość paska zamienimy szerokością szczeliny: <math>\varphi=\frac{2\pi}{\lambda}h sin\theta=2\alpha</math> , czyli <math>\alpha=\frac{\pi}{\lambda}h sin\theta</math> . | |||
W ten sposób różnica faz <math>\varphi\,</math> określona została przez mierzalne wielkości: szerokość szczeliny <math>h\,</math>, długość fali <math>\lambda\,</math> i kąt obserwacji <math>\theta\,</math>. Podstawiając wyznaczoną wypadkową różnicę faz do wzoru <math>E_{\theta}=E_0 \frac{sin\alpha}{\alpha}</math> , otrzymujemy wyrażenie na amplitudę fali wypadkowej. Intensywność obrazu dyfrakcyjnego proporcjonalna jest do kwadratu amplitudy. Zapiszmy więc kompletny wzór na rozkład intensywności obrazu dyfrakcyjnego zależny jedynie od mierzalnych wielkości, czyli umożliwiający weryfikację doświadczalną. Przez <math>I_{wzgl}\,</math> oznaczamy względną intensywność określoną jako stosunek intensywności dla danego kąta do intensywności maksymalnej, czyli dla kąta <math>\theta\,</math> równego zeru. | |||
Wersja z 19:42, 17 sie 2006

|
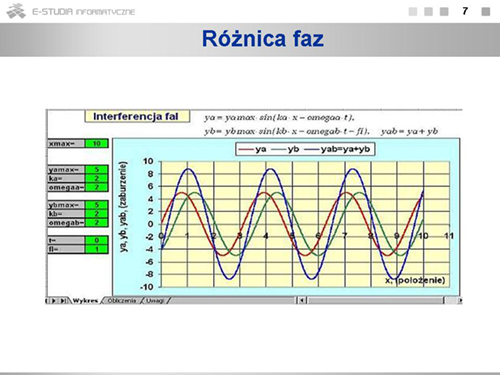
|
Kiedy inne parametry fal (na przykład częstość, amplituda) będą się różnić, fala wypadkowa nie musi być falą sinusoidalną. Możesz to sprawdzić sam, korzystając z załączonej ilustracji interaktywnej. |