PF Moduł 16

---

Wstęp Falowa natura światła była znana znacznie wcześniej niż odkryto, że jest ono falą elektromagnetyczną. Świadczyły o tym typowe zjawiska falowe, takie jak interferencja, czyli nakładanie się fal, czy dyfrakcja, czyli ugięcie na szczelinie. Warunkiem powstania trwałego obrazu interferencyjnego jest spójność światła, czyli niezmienna w czasie różnica faz między nakładającymi się falami. Naturalne źródła światła emitują światło niespójne, o przypadkowo zmieniającej się fazie. Z tego powodu nie możemy zaobserwować na ścianie wzmocnień i wygaszeń światła pochodzącego na przykład od dwóch żarówek. Takie wzmocnienia i wygaszenia wprawdzie powstają, ale ich położenia chaotycznie i szybko się zmieniają tak, że nasze oko rejestruje tylko jednolicie oświetloną płaszczyznę. Warunek spójności będzie spełniony, jeśli światło rozdzieli się, na przykład, podczas przejścia przez układ szczelin. Wtedy każda szczelina zgodnie zasadą Huyghensa będzie źródłem światła i będzie to światło spójne. W module tym omówimy zjawiska interferencji i dyfrakcji, a także efekty wynikające ze złożenia tych dwóch zjawisk. Pokażemy, jak opisane efekty można wykorzystać w siatce dyfrakcyjnej, a także do badania sieci krystalicznej przez wywołanie zjawiska dyfrakcji promieniowania rentgenowskiego na krysztale. Omówione zostanie również zjawisko Dopplera, dobrze każdemu znane z obserwacji dźwięków towarzyszących ruchowi ulicznemu.

---

Interferencja światła Doświadczenie Younga Z zasady superpozycji fal wynika, że jeśli dwie fale przemieszczają się w tym samym ośrodku, to powodowane przez nie zaburzenia w danym punkcie przestrzeni nakładają się, to znaczy, dodają lub odejmują się w zależności od tego, czy są tego samego czy różnego znaku. Zjawiska związane z nakładaniem się fal noszą nawę interferencji. Zjawisko interferencji dla fal świetlnych zostało po raz pierwszy zaobserwowane i zinterpretowane jako przejaw falowej natury światła przez Thomasa Younga w 1801 roku. Uproszczony schemat doświadczenia Younga przedstawia rysunek. Światło w postaci fali płaskiej pada na układ dwóch szczelin $S_1$ i $S_2$ w przesłonie $P$. Interesuje nas rezultat nałożenia się fal w punkcie $A$ na ekranie $E$ ustawionym za szczelinami. Światło padające symbolizują równoległe niebieskie linie (powierzchnie falowe) i strzałki (promienie) z lewej strony. Promienie świetlne, które przeszły przez szczeliny $S_1$ i $S_2$ docierają do punktu $A$, ale drogi ich $r_1$ i $r_2$ nie są takie same. Jeśli więc faza fali świetlnej była w płaszczyźnie szczelin taka sama, to w punkcie $A$ będzie różna wskutek różnicy dróg. Warunek wzmocnienia lub wygaszenia wynika z geometrycznych zależności zilustrowanych na rysunku. Trzeba tu zwrócić uwagę, że w rzeczywistości odległość ekranu od przesłony jest o wiele większa niż odległość pomiędzy szczelinami tzn. $H>>d$ . W takim przypadku promienie $r_1$ i $r_2$ są z dobrym przybliżeniem równoległe, a trójkąty $SBA$ i $S_{1}a{S}_2$ możemy uznać za podobne, co z kolei oznacza, że kąty $ASB$ i $S_2{S}_{1}a$ są sobie równe. Kąt $ASB$, który może być łatwo zmierzony, oznaczyliśmy symbolem $\theta$. Różnica dróg promieni od szczelin do punktu $A$ równa jest $dsin\theta$. Jeśli różnica ta będzie równa całkowitej wielokrotności długości fali, to nastąpi wzmocnienie, jeśli równa będzie równa nieparzystej wielokrotności połowy długości fali - nastąpi wygaszenie. Warunek uzyskania maksimum natężenia fali wypadkowej zapiszemy w postaci: $dsin\theta =n\lambda$ , warunek uzyskania minimum, czyli wygaszenia: $dsin\theta =(2n+1)\frac{\lambda }{2}=(n+\frac{1}{2})\lambda$

---

Z postaci wzorów widzimy, że im mniejsza jest odległość pomiędzy szczelinami tym większa będzie wartość kąta, dla którego wystąpi wzmocnienie (lub wygaszenie) i tym większa będzie różnica kątowa pomiędzy maksimami bądź minimami. Rysunek przedstawia ilustrację interferencji w doświadczeniu Younga dla dwóch różnych odległości pomiędzy szczelinami; z lewej - mniejszej, z prawej - większej.

---

Uogólnijmy nasze rozważania. Rozpatrzmy dwie fale o tych samych amplitudach i częstościach, ale różniące się fazą: $y_1=y_{0}sin(kx-\omega t)$ oraz $y_1=y_{0}sin(kx-\omega t-\phi )$. Jak wspominaliśmy już, w przypadku fal elektromagnetycznych, jako zaburzenie y traktujemy zazwyczaj wartość wektora natężenia pola elektrycznego. Zgodnie z zasadą superpozycji fal, zaburzenie wypadkowe w danym punkcie przestrzeni i momencie czasu będzie sumą zaburzeń pochodzących od obu fal $y_{12}=y_1+y_2$. Po zastosowaniu trygonometrycznego wzoru na sumę sinusów, otrzymujemy: $y_{12}=y_0[2sin(kx-\omega t-\phi )cos\frac{\phi }{2}]$

---

We wzorze na $y_{12}$ możemy wyodrębnić czynnik niezależny od czasu i położenia. Jest to amplituda równa $2y_{0}cos\frac{\phi }{2}$. Amplituda ta zależy od $\phi$, czyli różnicy faz pomiędzy falami. Maksymalna amplituda równa będzie podwojonej amplitudzie fal składowych, co nastąpi, kiedy różnica faz będzie równa zeru. Amplituda równa zeru będzie dla różnicy faz równej $\pi$, wtedy przeciwne w fazie zaburzenia będą się wzajemnie znosić. Dla innych różnic faz amplituda będzie przyjmować wartości pośrednie.

---

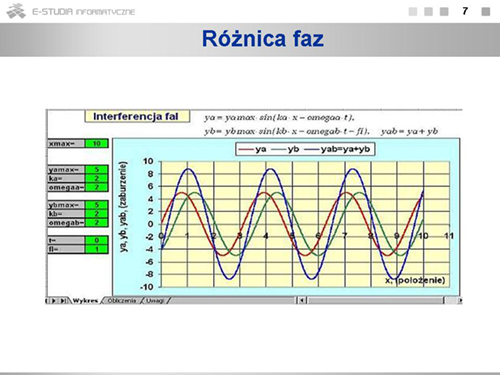
Kiedy inne parametry fal (na przykład częstość, amplituda) będą się różnić, fala wypadkowa nie musi być falą sinusoidalną. Możesz to sprawdzić sam, korzystając z załączonej ilustracji interaktywnej.

---

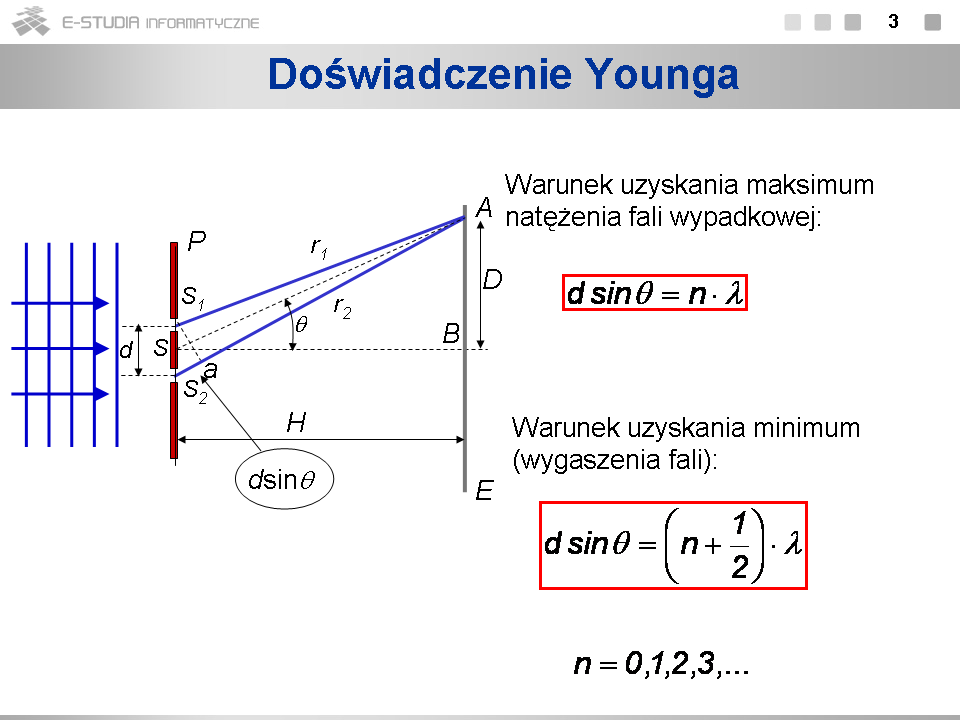
Na zakończenie dwie uwagi: W praktyce, dla spełnienia zarówno warunków równoległości promieni jak i skończonej odległości $H$ pomiędzy przesłoną i ekranem, stosuje się zwykle soczewkę skupiającą równoległe promienie w płaszczyźnie ogniskowej, gdzie umieszcza się ekran; Założyliśmy tu milcząco, że szerokość szczeliny jest zaniedbywanie mała w stosunku do odległości pomiędzy szczelinami. Przypadek ogólny, kiedy obie te wielkości są porównywalne, rozpatrzymy w następnej części tej lekcji omawiając zjawiska dyfrakcji.