PF Moduł 15: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 248: | Linia 248: | ||
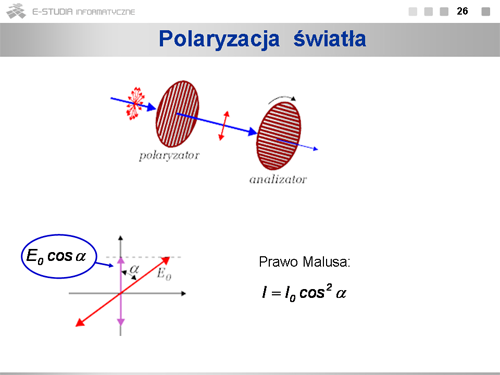
Przy kątach pośrednich natężenie przechodzącego światła będzie się zmieniać zgodnie z tzw. '''prawem Malusa'''. Sens tego prawa wyjaśnia schemat pokazany na rysunku. Jeśli czerwona strzałka pokazuje kierunek drgań wektora pola elektrycznego po przejściu światła przez polaryzator, to przy ustawieniu analizatora zgodnie ze strzałką fioletową składowa drgań po przejściu przez niego będzie <math>E_0 cos\alpha\,</math>. Natężenie promieniowania proporcjonalne jest do kwadratu amplitudy drgań, więc zależność natężenia (intensywności) promieniowania od kąta może być wyrażona w postaci <math>l=l_0 cos^2 \alpha</math>. | Przy kątach pośrednich natężenie przechodzącego światła będzie się zmieniać zgodnie z tzw. '''prawem Malusa'''. Sens tego prawa wyjaśnia schemat pokazany na rysunku. Jeśli czerwona strzałka pokazuje kierunek drgań wektora pola elektrycznego po przejściu światła przez polaryzator, to przy ustawieniu analizatora zgodnie ze strzałką fioletową składowa drgań po przejściu przez niego będzie <math>E_0 cos\alpha\,</math>. Natężenie promieniowania proporcjonalne jest do kwadratu amplitudy drgań, więc zależność natężenia (intensywności) promieniowania od kąta może być wyrażona w postaci <math>l=l_0 cos^2 \alpha</math>. | ||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="450px" valign="top"|[[Grafika:PF1_M15_Slajd27.png]] | |||
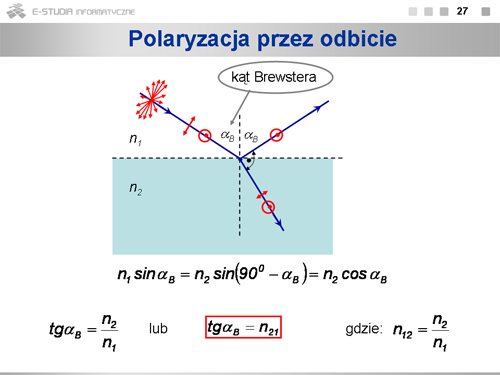
|valign="top"|Kiedy nie spolaryzowane światło pada na granicę dwóch ośrodków to światło odbite wykazuje pewien stan polaryzacji. Całkowita polaryzacja jest wtedy, kiedy kąt pomiędzy wiązką odbitą i załamaną jest kątem prostym. Kąt padania <math>\alpha\,</math>, dla którego warunek ten jest spełniony nosi nazwę '''kąta Brewstera'''. Światło załamane jest spolaryzowane w dużym stopniu w kierunku prostopadłym do kierunku polaryzacji światła odbitego. Jednak nawet przy kącie padania równym kątowi Brewstera światło to nie jest spolaryzowane całkowicie. Kiedy kąt padania równy jest kątowi Brewstera, to wykorzystując prawo załamania Sneliusa otrzymujemy: <math>tg\alpha_B=n_{21}</math>. Wielkość <math>n_{21}\,</math> określa współczynnik załamania ośrodka drugiego względem pierwszego. Określenie kąta Brewstera umożliwia znalezienie warunków, w jakich następuje całkowita polaryzacja promienia odbitego. | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="450px" valign="top"|[[Grafika:PF1_M15_Slajd28.png]] | |||
|valign="top"|'''Podwójne załamanie lub dwójłomność''', to rozdzielenie światła padającego na kryształ o strukturze nieregularnej na dwa promienie rozchodzące się z różnymi prędkościami. Kryształy dwójłomne dzielą się na jedno- i dwuosiowe. W kryształach jednoosiowych jeden promień podlega znanemu nam prawu załamania. Promień ten nazywamy '''promieniem zwyczajnym'''. Drugi promień nie zachowuje stałego stosunku sinusów kąta padania i załamania, kiedy zmienia się kąt padania. Nawet kiedy światło pada prostopadle do powierzchni kryształu następuje odchylenie tego promienia, który w związku ze swymi własnościami nazywamy '''promieniem nadzwyczajnym'''. W kryształach jednoosiowych istnieje jednak kierunek, wzdłuż którego oba promienie poruszają się z jednakową prędkością. Kierunek taki nazywamy osią optyczną kryształu. (W kryształach dwuosiowych istnieją dwa takie kierunki.) Promienie: zwyczajny i nadzwyczajny spolaryzowane są w płaszczyznach do siebie prostopadłych. Istnieją kryształy, w których jeden z promieni pochłaniany jest silniej niż drugi. Zjawisko to zwane dichroizmem wykorzystywane jest w konstrukcji przyrządów polaryzacyjnych. | |||
Wyjaśnienie natury dwójłomności, która pozwala nam uzyskać światło spolaryzowane, wiąże się z własnościami kryształów dwójłomnych, w których przenikalność elektryczna zależna jest od kierunku. Jak wiemy, wartość przenikalności elektrycznej określa współczynnik załamania <math>(n \approx \sqrt{\varepsilon})</math>, a co za tym idzie - prędkość światła w danym kierunku. | |||
Istnieją też substancje, zwane optycznie czynnymi, mające zdolność skręcania płaszczyzny polaryzacji światła spolaryzowanego, które przez nie przechodzi. W kryształach skręcenie jest najsilniejsze, gdy światło biegnie wzdłuż osi optycznej kryształu. Kąt skręcenia zwiększa się proporcjonalnie do drogi, jaką światło przebywa w krysztale. Współczynnik tej proporcjonalności nazywa się stałą skręcenia. W roztworach kąt skręcenia proporcjonalny jest też do koncentracji substancji czynnej. W tym przypadku współczynnik proporcjonalności nazywa się zdolnością skręcającą. | |||
Wersja z 12:04, 17 sie 2006

|

|
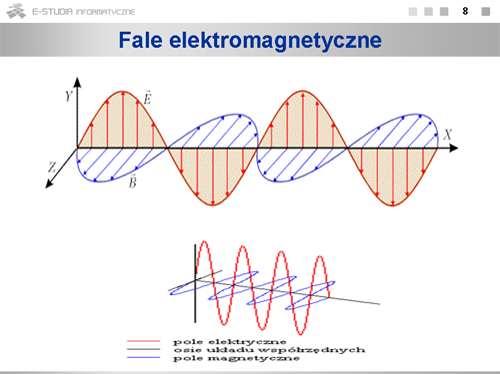
Nasze rozważania rozpoczniemy od przypomnienia równań Maxwella, które przedstawiają relacje pomiędzy zmianami pól: elektrycznego i magnetycznego w czasie i przestrzeni. |

|
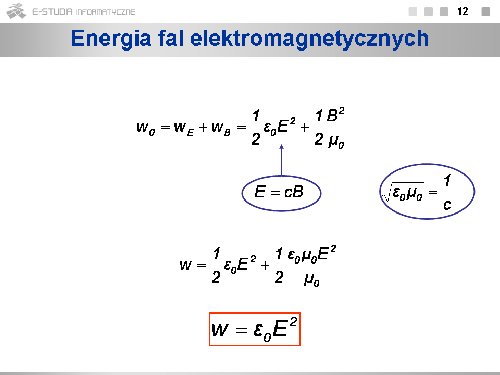
Możemy też gęstość energii fali elektromagnetycznej przedstawić w postaci: lub . |