PF Moduł 15: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 225: | Linia 225: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="450px" valign="top"|[[Grafika:PF1_M15_Slajd24.png]] | |width="450px" valign="top"|[[Grafika:PF1_M15_Slajd24.png]] | ||
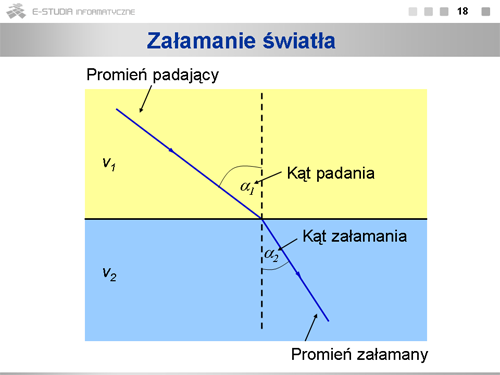
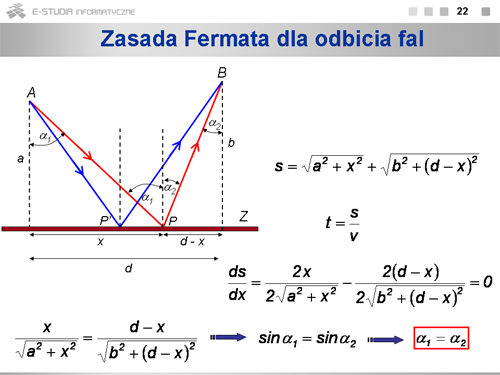
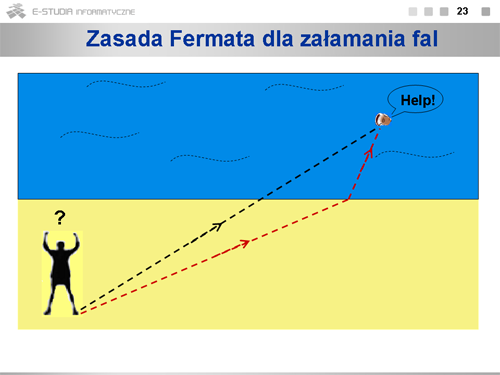
|valign="top"|Zastosujmy zasadę Fermata do zjawiska załamania fali na granicy dwóch ośrodków o współczynnikach załamania <math>n_1\,</math> i <math>n_2\,</math>. Relacje geometryczne przedstawia rysunek. Pamiętając, że współczynnik załamania jest stosunkiem prędkości światła w próżni do prędkości w danym ośrodku <math>n=\frac{c}{v}</math>, otrzymujemy wyrażenie na czas przebycia przez światło drogi od <math>A\,</math> do <math>B\,</math>: <math>t=\frac{n_1 l_1+n_2 l_2}{c}</math>. Wielkość <math>l=n_1 l_1+n_2 l_2</math> nosi nazwę drogi optycznej. Poszukujemy więc takiej wartości <math>x\,</math>, przy ustalonych położeniach punktów <math>A\,</math> i <math>B\,</math>, by droga optyczna była minimalna. W tym celu obliczamy pochodną wyrażenia, w którym drogę optyczną określamy w funkcji <math>x\,</math>: <math>l=n_1\sqrt{a^2+x^2}+n_2\sqrt{b^2+(c-x)^2}</math>. Po przyrównaniu pochodnej <math>dl/dx\,</math> do zera otrzymujemy: <math>n_1\frac{x}{\sqrt{a^2+x^2}}=n_2\frac{c-x}{\sqrt{b^2+(c-x)^2}}</math>, czyli znane prawo załamania: <math>n_1 sin\alpha_1=n_2 sin\alpha_2</math>. | |valign="top"|Zastosujmy zasadę Fermata do zjawiska załamania fali na granicy dwóch ośrodków o współczynnikach załamania <math>n_1\,</math> i <math>n_2\,</math>. Relacje geometryczne przedstawia rysunek. Pamiętając, że współczynnik załamania jest stosunkiem prędkości światła w próżni do prędkości w danym ośrodku <math>n=\frac{c}{v}</math>, otrzymujemy wyrażenie na czas przebycia przez światło drogi od <math>A\,</math> do <math>B\,</math>: <math>t=\frac{n_1 l_1+n_2 l_2}{c}</math>. Wielkość <math>l=n_1 l_1+n_2 l_2</math> nosi nazwę drogi optycznej. Poszukujemy więc takiej wartości <math>x\,</math>, przy ustalonych położeniach punktów <math>A\,</math> i <math>B\,</math>, by droga optyczna była minimalna. W tym celu obliczamy pochodną wyrażenia, w którym drogę optyczną określamy w funkcji <math>x\,</math>: <math>l=n_1\sqrt{a^2+x^2}+n_2\sqrt{b^2+(c-x)^2}</math>. Po przyrównaniu pochodnej <math>dl/dx\,</math> do zera otrzymujemy: <math>n_1\cdot\frac{x}{\sqrt{a^2+x^2}}=n_2\cdot\frac{c-x}{\sqrt{b^2+(c-x)^2}}</math>, czyli znane prawo załamania: <math>n_1 sin\alpha_1=n_2 sin\alpha_2</math>. | ||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="450px" valign="top"|[[Grafika:PF1_M15_Slajd25.png]] | |||
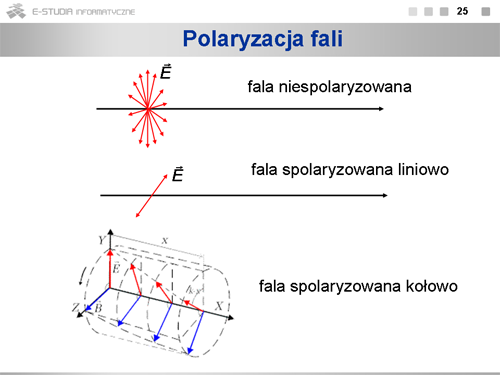
|valign="top"|'''Polaryzacja fali''' | |||
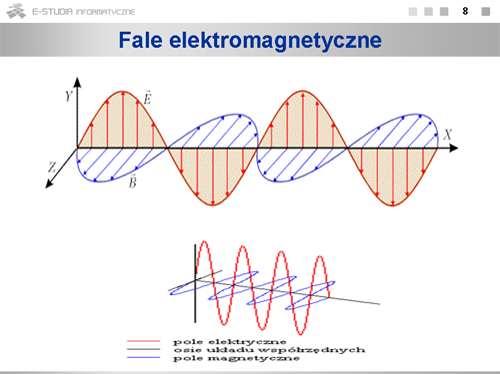
W świetle naturalnym, czyli emitowanym przez naturalne źródła takie jak żarówka lub słońce, wektor drga we wszystkich możliwych kierunkach prostopadłych do promienia. Na promieniowanie ciała świecącego składają się fale emitowane przez poszczególne atomy. Ponieważ emisja atomów odbywa się niezależnie od siebie, płaszczyzna drgań wektora <math>\overrightarrow{E}\,</math> zorientowana zupełnie przypadkowo. W fali wypadkowej drgania o różnych kierunkach występują z jednakowym prawdopodobieństwem. Taką falę nazywamy falą niespolaryzowaną. Jeśli kierunki drgań wektora <math>\overrightarrow{E}\,</math> są w jakiś sposób uporządkowane, falę nazywamy spolaryzowaną. Polaryzacja może być liniowa, gdy drgania zachodzą tylko w jednej przechodzącej przez promień płaszczyźnie. Kiedy z zachowaniem wzajemnych relacji kierunkowych, układ wektorów <math>\overrightarrow{E}\,</math> i <math>\overrightarrow{B}\,</math> wykonuje obrót wokół kierunku propagacji, to mówimy, że fala jest spolaryzowana kołowo. W zależności od kierunku tego obrotu fala może być spolaryzowana prawo- lub lewoskrętnie. W przypadku fali spolaryzowanej kołowo składowe <math>Y\,</math> i <math>Z\,</math> wektorów <math>\overrightarrow{E}\,</math> i <math>\overrightarrow{B}\,</math> będą różne w różnych punktach na osi <math>X\,</math>, przy zachowaniu bezwzględnych ich wartości. Kiedy bezwzględne wartości zmieniają się, mówimy o polaryzacji eliptycznej. | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="450px" valign="top"|[[Grafika:PF1_M15_Slajd26.png]] | |||
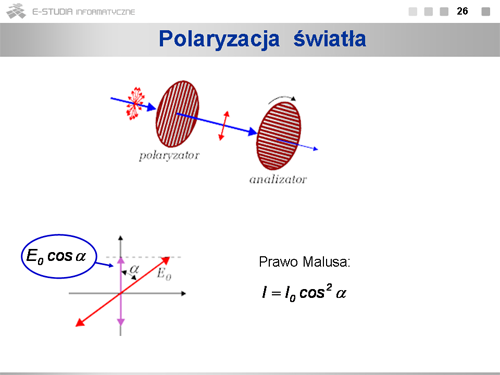
|valign="top"|Czy można "spolaryzować" światło? Gdybyśmy umieli z przypadkowo zorientowanych ciągów falowych wydzielić tylko takie, które mają zadaną stałą płaszczyznę drgań wektora elektrycznego, to moglibyśmy otrzymać światło spolaryzowane. Intuicja podpowiada nam, że w tym celu musimy światło skierować na obiekt mający własności kierunkowe w płaszczyźnie prostopadłej do kierunku rozchodzenia się fali świetlnej. Sposobów uzyskania światła spolaryzowanego jest wiele i omówimy tu niektóre z nich. | |||
'''Polaroid''' - to płytka lub błona, w której cząsteczki ułożone są tak, że tworzą strukturę łańcuchową, która po zabiegach mechanicznych i chemicznych, przepuszcza jedynie składową wektora <math>\overrightarrow{E}\,</math> równoległą do wyróżnionego kierunku w płytce. Kiedy drugą taką płytkę będziemy obracać wokół osi równoległej do kierunku padania światła zauważymy, że światło zostało spolaryzowane, bo natężenie światła przepuszczonego będzie się zmieniać. Kiedy płytki ustawimy tak, że ich kierunki polaryzacji będą się krzyżować pod kątem prostym uzyskamy wygaszenie fal, kiedy kierunki te będą równoległe, uzyskamy maksymalne przepuszczanie światła. Oznacza to, że w pierwszej płytce światło zostało liniowo spolaryzowane. | |||
Przy kątach pośrednich natężenie przechodzącego światła będzie się zmieniać zgodnie z tzw. '''prawem Malusa'''. Sens tego prawa wyjaśnia schemat pokazany na rysunku. Jeśli czerwona strzałka pokazuje kierunek drgań wektora pola elektrycznego po przejściu światła przez polaryzator, to przy ustawieniu analizatora zgodnie ze strzałką fioletową składowa drgań po przejściu przez niego będzie <math>E_0 cos\alpha\,</math>. Natężenie promieniowania proporcjonalne jest do kwadratu amplitudy drgań, więc zależność natężenia (intensywności) promieniowania od kąta może być wyrażona w postaci <math>l=l_0 cos^2 \alpha</math>. | |||
Wersja z 11:56, 17 sie 2006

|

|
Nasze rozważania rozpoczniemy od przypomnienia równań Maxwella, które przedstawiają relacje pomiędzy zmianami pól: elektrycznego i magnetycznego w czasie i przestrzeni. |

|
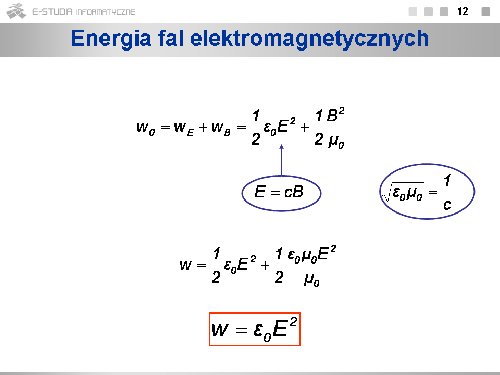
Możemy też gęstość energii fali elektromagnetycznej przedstawić w postaci: lub . |