PF Moduł 15: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 168: | Linia 168: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="450px" valign="top"|[[Grafika:PF1_M15_Slajd18.png]] | |width="450px" valign="top"|[[Grafika:PF1_M15_Slajd18.png]] | ||
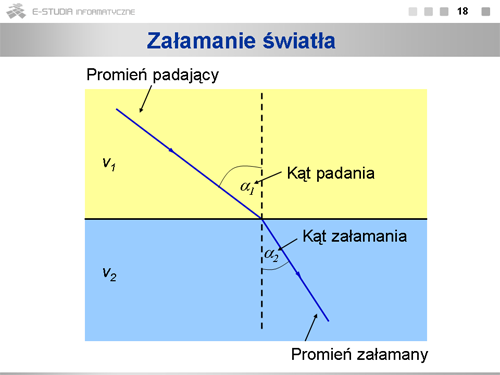
|valign="top"|Zastosujmy zasadę Huyghensa do zjawiska załamania światła na granicy dwóch ośrodków. W pierwszym prędkość światła wynosi <math>v_1\,</math>, w drugim <math> | |valign="top"|Zastosujmy zasadę Huyghensa do zjawiska załamania światła na granicy dwóch ośrodków. W pierwszym prędkość światła wynosi <math>v_1\,</math>, w drugim <math>v_2\,</math>. Kąty padania i załamania definiujemy jako kąty między normalną do granicy ośrodków a odpowiednio, promieniem padającym i załamanym. | ||
|} | |} | ||
| Linia 176: | Linia 176: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="450px" valign="top"|[[Grafika:PF1_M15_Slajd19.png]] | |width="450px" valign="top"|[[Grafika:PF1_M15_Slajd19.png]] | ||
|valign="top"|Niech czoło fali rozchodzącej się w prędkością <math>v_1\,</math> w pierwszym ośrodku o współczynniku załamania <math>n_1\,</math>, pada na granicę z drugim ośrodkiem o współczynniku załamania <math>n_2\,</math> i rozchodzi się dalej z prędkością <math>v_2\,</math>. Zgodnie z zasadą Huyghensa, w ośrodku tym rozchodzą się fale kuliste, które na rysunku pokazane są kolorem czerwonym. W czasie, kiedy światło przebiegnie w ośrodku pierwszym odcinek <math>AA'\,</math>, fala w ośrodku drugim przebiegnie odcinek <math>BB'\,</math>: <math>t_{AA'}=t_{BB'}</math>. Wyrażając czas jako iloraz drogi i prędkości mamy: <math>\frac{AA'}{v_1}=\frac{BB'}{v_2}</math> Pamiętamy przy tym, że współczynnik załamania wiąże się z prędkością fali związkiem . | |valign="top"|Niech czoło fali rozchodzącej się w prędkością <math>v_1\,</math> w pierwszym ośrodku o współczynniku załamania <math>n_1\,</math>, pada na granicę z drugim ośrodkiem o współczynniku załamania <math>n_2\,</math> i rozchodzi się dalej z prędkością <math>v_2\,</math>. Zgodnie z zasadą Huyghensa, w ośrodku tym rozchodzą się fale kuliste, które na rysunku pokazane są kolorem czerwonym. W czasie, kiedy światło przebiegnie w ośrodku pierwszym odcinek <math>AA'\,</math>, fala w ośrodku drugim przebiegnie odcinek <math>BB'\,</math>: <math>t_{AA'}=t_{BB'}</math>. Wyrażając czas jako iloraz drogi i prędkości mamy: <math>\frac{AA'}{v_1}=\frac{BB'}{v_2}</math> Pamiętamy przy tym, że współczynnik załamania wiąże się z prędkością fali związkiem <math>n=\frac{c}{v}</math>. | ||
Wykorzystując zależności geometryczne: <math>AA'=BA'sin\alpha_1</math> i <math>BB'=BA'sin\alpha_2</math>, otrzymujemy prawo Sneliusa: <math>n_1 sin\alpha_1=n_2 sin\alpha_2</math>, które można też wyrazić jako: stosunek sinusa kąta padania do sinusa kąta załamania jest stały i równy współczynnikowi załamania ośrodka drugiego względem pierwszego. | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="450px" valign="top"|[[Grafika:PF1_M15_Slajd20.png]] | |||
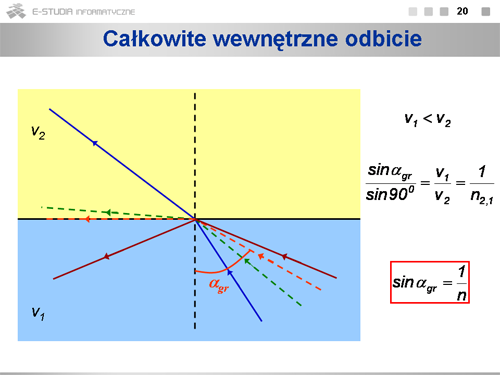
|valign="top"|Jeśli promień padający biegnie w ośrodku gęstszym optycznie (czyli <math>v_1<v_2</math>), to kąt załamania jest większy niż kąt padania. Zwiększając kąt padania dochodzimy do sytuacji, gdy kąt załamania równy jest <math>90^\circ\,</math>. Taki kąt padania nazywamy kątem granicznym. Sinus kąta granicznego jest odwrotnością współczynnika załamania ośrodka gęstszego optyczne względem ośrodka rzadszego optycznie. Jeśli światło padnie na granicę ośrodków pod kątem większym od granicznego, odbije się w całości od granicy. Jest to zjawisko całkowitego wewnętrznego odbicia. Wykorzystywane jest ono w konstrukcji światłowodów. | |||
Wersja z 11:24, 17 sie 2006

|

|
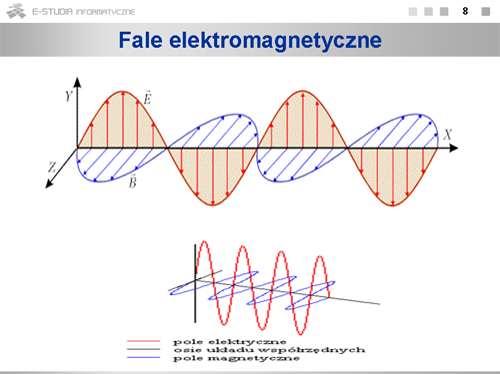
Nasze rozważania rozpoczniemy od przypomnienia równań Maxwella, które przedstawiają relacje pomiędzy zmianami pól: elektrycznego i magnetycznego w czasie i przestrzeni. |

|
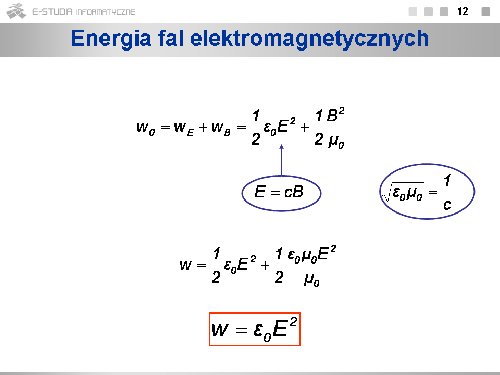
Możemy też gęstość energii fali elektromagnetycznej przedstawić w postaci: lub . |