PF Moduł 15: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 144: | Linia 144: | ||
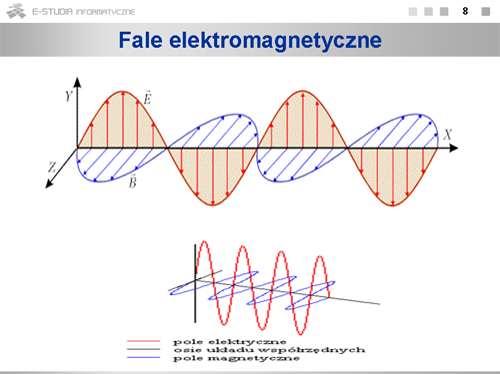
Rozchodzenie się światła, podobnie jak i fal elektromagnetycznych o innych długościach, polega na przemieszczaniu się w czasie i przestrzeni drgań wektorów natężeń pól: elektrycznego i magnetycznego. Prędkość światła w próżni oznaczyliśmy symbolem <math>c\,</math>. Jak stwierdziliśmy, w innych ośrodkach prędkość ta jest mniejsza, co wynika z równań Maxwella, i zależy od względnej przenikalności elektrycznej <math>\varepsilon\,</math> i magnetycznej <math>\mu\,</math> ośrodka. Współczynnik załamania światła w ośrodku definiujemy wzorem <math>n=\frac{c}{v}</math>, a więc prędkość światła w danym ośrodku można wyrazić następująco: <math>n=\sqrt{\varepsilon \mu}\approx \sqrt{\varepsilon}</math>. Przybliżona równość w tym wzorze wynika z faktu, że dla większości ośrodków, w których rozważamy rozchodzenie się światła, wartość przenikalności magnetycznej jest na tyle bliska jedności, że można ją tu pominąć. Otrzymujemy w ten sposób wynikającą z równań Maxwella interesującą zależność między współczynnikiem załamania i przenikalnością elektryczną dla większości (nie ferromagnetycznych) ośrodków <math>n\approx \sqrt{\varepsilon}</math>. Dodajmy do tego jeszcze, że chociaż w falach elektromagnetycznych mamy do czynienia z drganiami wektorów <math>\overrightarrow{E}\,</math> i <math>\overrightarrow{B}\,</math>, to doświadczalnie stwierdzono decydującą rolę drgań pola elektrycznego dla reakcji fotochemicznych, fotoelektrycznych czy również fizjologicznych. Dlatego w rozważaniach naszych będziemy mówić o drganiach wektora natężenia pola elektrycznego jako o drganiach wektora świetlnego. Stosunek prędkości światła w próżni do prędkości światła w danym ośrodku oznaczyliśmy symbolem <math>n\,</math> i nazywamy współczynnikiem załamania. Często nazywa się go także bezwzględnym współczynnikiem załamania, gdyż określa załamanie światła przy przejściu z próżni do ośrodka. Jeśli światło przechodzi z ośrodka <math>1\,</math>, gdzie rozchodzi się z prędkością <math>v_1\,</math> do ośrodka <math>2\,</math>, gdzie prędkość światła wynosi <math>v_2\,</math>, załamanie jest określone przez współczynnik załamania ośrodka drugiego względem ośrodka pierwszego <math>n_{2,1}=\frac{n_2}{n_1}=\frac{v_1}{v_2}</math>. | Rozchodzenie się światła, podobnie jak i fal elektromagnetycznych o innych długościach, polega na przemieszczaniu się w czasie i przestrzeni drgań wektorów natężeń pól: elektrycznego i magnetycznego. Prędkość światła w próżni oznaczyliśmy symbolem <math>c\,</math>. Jak stwierdziliśmy, w innych ośrodkach prędkość ta jest mniejsza, co wynika z równań Maxwella, i zależy od względnej przenikalności elektrycznej <math>\varepsilon\,</math> i magnetycznej <math>\mu\,</math> ośrodka. Współczynnik załamania światła w ośrodku definiujemy wzorem <math>n=\frac{c}{v}</math>, a więc prędkość światła w danym ośrodku można wyrazić następująco: <math>n=\sqrt{\varepsilon \mu}\approx \sqrt{\varepsilon}</math>. Przybliżona równość w tym wzorze wynika z faktu, że dla większości ośrodków, w których rozważamy rozchodzenie się światła, wartość przenikalności magnetycznej jest na tyle bliska jedności, że można ją tu pominąć. Otrzymujemy w ten sposób wynikającą z równań Maxwella interesującą zależność między współczynnikiem załamania i przenikalnością elektryczną dla większości (nie ferromagnetycznych) ośrodków <math>n\approx \sqrt{\varepsilon}</math>. Dodajmy do tego jeszcze, że chociaż w falach elektromagnetycznych mamy do czynienia z drganiami wektorów <math>\overrightarrow{E}\,</math> i <math>\overrightarrow{B}\,</math>, to doświadczalnie stwierdzono decydującą rolę drgań pola elektrycznego dla reakcji fotochemicznych, fotoelektrycznych czy również fizjologicznych. Dlatego w rozważaniach naszych będziemy mówić o drganiach wektora natężenia pola elektrycznego jako o drganiach wektora świetlnego. Stosunek prędkości światła w próżni do prędkości światła w danym ośrodku oznaczyliśmy symbolem <math>n\,</math> i nazywamy współczynnikiem załamania. Często nazywa się go także bezwzględnym współczynnikiem załamania, gdyż określa załamanie światła przy przejściu z próżni do ośrodka. Jeśli światło przechodzi z ośrodka <math>1\,</math>, gdzie rozchodzi się z prędkością <math>v_1\,</math> do ośrodka <math>2\,</math>, gdzie prędkość światła wynosi <math>v_2\,</math>, załamanie jest określone przez współczynnik załamania ośrodka drugiego względem ośrodka pierwszego <math>n_{2,1}=\frac{n_2}{n_1}=\frac{v_1}{v_2}</math>. | ||
Pod pojęciem natężenia lub intensywności fali świetlnej będziemy tu rozumieć wielkość proporcjonalną nie do amplitudy drgań wektora <math>\overrightarrow{E}\,</math>, a do kwadratu tej amplitudy, bowiem, jak pamiętamy, energia fali elektromagnetycznej jest proporcjonalna do kwadratu natężenia pola elektrycznego. Pod sformułowaniem "amplituda fali" będziemy więc rozumieli, amplitudę drgań elektrycznych zaś w celu wyznaczenia intensywności lub natężenia światła będziemy wyznaczać wielkość proporcjonalną do kwadratu amplitudy. | |||
Wszystkie omawiane tu zjawiska mogą być opisane z użyciem formalizmu równań Maxwella. Zjawiska te i prawidłowości nimi rządzące zostały jednak zaobserwowane znacznie wcześniej. Zostały one opisane w ramach fenomenologicznych zasad, które umożliwiały w prosty sposób zrozumienie zjawisk falowych nie rozpatrując elektromagnetycznej natury samych fal, z czego nie zdawano sobie wcześniej sprawy. Jak już powiedzieliśmy, dopiero Maxwell pokazał, że światło ma naturę fal elektromagnetycznych. | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="450px" valign="top"|[[Grafika:PF1_M15_Slajd17.png]] | |||
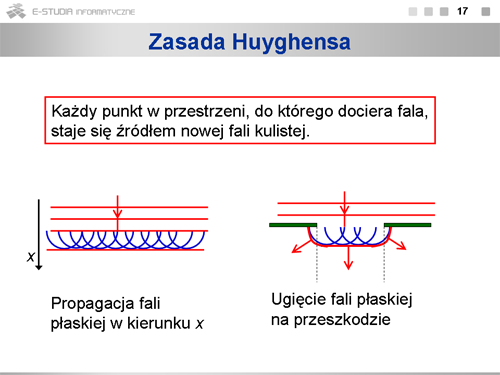
|valign="top"|Prosty opis wielu zjawisk falowych umożliwia zasada podana przez Christiana Huyghensa w 1678 roku, a więc prawie dwa wieki przed sformułowaniem przez Maxwella równań fal elektromagnetycznych. Zasada ta nie zakłada elektromagnetycznego charakteru fal świetlnych i nie wymaga znajomości prędkości ich rozchodzenia się. Mimo to jest niezwykle użyteczna do opisu wielu zjawisk obserwowanych w optyce. Warto dodać, że zasada ta ma charakter ogólny i może być stosowana do opisu różnego rodzaju fal. | |||
Zasadę Huyghensa można sformułować następująco: Każdy punkt w przestrzeni, do którego dociera fala, staje się źródłem nowej fali kulistej. | |||
Zasada ta nie jest w sprzeczności z prostoliniowym rozchodzeniem się światła, bowiem złożenie fal kulistych daje w rezultacie czoło fali rozchodzące się w określonym kierunku. | |||
Wyjaśnia również zjawisko ugięcia światła na przeszkodzie, czy po przejściu przez otwór. Jeśli na płaską przegrodę z otworem pada fala płaska w kierunku prostopadłym do przegrody, to każdy punkt otworu staje się źródłem wtórnej fali kulistej. Obwiednia tych fal wtórnych wyznacza nowe czoło fali. Widzimy, że fala przenika w obszar cienia geometrycznego, zaznaczonego na rysunku linią przerywaną. | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="450px" valign="top"|[[Grafika:PF1_M15_Slajd18.png]] | |||
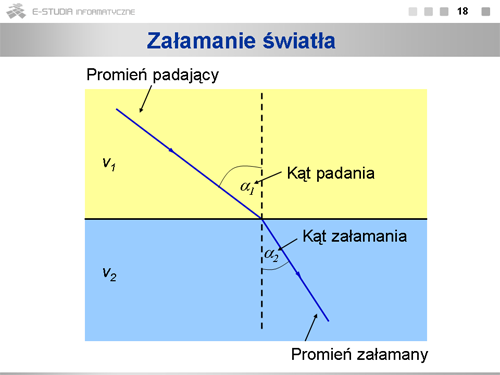
|valign="top"|Zastosujmy zasadę Huyghensa do zjawiska załamania światła na granicy dwóch ośrodków. W pierwszym prędkość światła wynosi <math>v_1\,</math>, w drugim <math>v2\,</math>. Kąty padania i załamania definiujemy jako kąty między normalną do granicy ośrodków a odpowiednio, promieniem padającym i załamanym. | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="450px" valign="top"|[[Grafika:PF1_M15_Slajd19.png]] | |||
|valign="top"|Niech czoło fali rozchodzącej się w prędkością <math>v_1\,</math> w pierwszym ośrodku o współczynniku załamania <math>n_1\,</math>, pada na granicę z drugim ośrodkiem o współczynniku załamania <math>n_2\,</math> i rozchodzi się dalej z prędkością <math>v_2\,</math>. Zgodnie z zasadą Huyghensa, w ośrodku tym rozchodzą się fale kuliste, które na rysunku pokazane są kolorem czerwonym. W czasie, kiedy światło przebiegnie w ośrodku pierwszym odcinek <math>AA'\,</math>, fala w ośrodku drugim przebiegnie odcinek <math>BB'\,</math>: <math>t_{AA'}=t_{BB'}</math>. Wyrażając czas jako iloraz drogi i prędkości mamy: <math>\frac{AA'}{v_1}=\frac{BB'}{v_2}</math> Pamiętamy przy tym, że współczynnik załamania wiąże się z prędkością fali związkiem . | |||
Wersja z 11:16, 17 sie 2006

|

|
Nasze rozważania rozpoczniemy od przypomnienia równań Maxwella, które przedstawiają relacje pomiędzy zmianami pól: elektrycznego i magnetycznego w czasie i przestrzeni. |

|
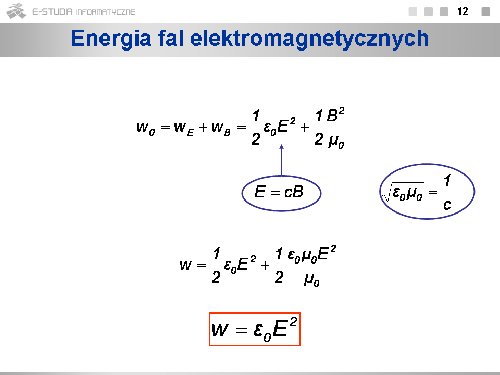
Możemy też gęstość energii fali elektromagnetycznej przedstawić w postaci: lub . |