PF Moduł 15: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 134: | Linia 134: | ||
|width="450px" valign="top"|[[Grafika:PF1_M15_Slajd15.png]] | |width="450px" valign="top"|[[Grafika:PF1_M15_Slajd15.png]] | ||
|valign="top"|Wykorzystując związki: <math>E=cB</math> oraz <math>c=\frac{1}{\sqrt{\varepsilon_0 \mu_0}}</math> możemy wzór na energię przenoszona przez jednostkową powierzchnię w jednostce czasu przedstawić jako: <math>P=\frac{EB}{\mu_0}</math>. Ponieważ, jak to już stwierdziliśmy, energia ta przenoszona jest w kierunku prostopadłym do wektorów <math>\overrightarrow{E}\,</math> i <math>\overrightarrow{B}\,</math>, możemy zdefiniować wektor, którego wartość określa energię przenoszoną przez jednostkową powierzchnię w jednostce czasu, a kierunek wskazuje kierunek przenoszenia tej energii. Pamiętając, że wektory <math>\overrightarrow{E}\,</math> i <math>\overrightarrow{B}\,</math> są do siebie prostopadłe zapisujemy wzór w postaci wektorowej: <math>\overrightarrow{P}=\frac{1}{\mu_0}\overrightarrow{E}\times \overrightarrow{B}</math>. Określony tym wzorem wektor nosi nazwę wektora Poyntinga. | |valign="top"|Wykorzystując związki: <math>E=cB</math> oraz <math>c=\frac{1}{\sqrt{\varepsilon_0 \mu_0}}</math> możemy wzór na energię przenoszona przez jednostkową powierzchnię w jednostce czasu przedstawić jako: <math>P=\frac{EB}{\mu_0}</math>. Ponieważ, jak to już stwierdziliśmy, energia ta przenoszona jest w kierunku prostopadłym do wektorów <math>\overrightarrow{E}\,</math> i <math>\overrightarrow{B}\,</math>, możemy zdefiniować wektor, którego wartość określa energię przenoszoną przez jednostkową powierzchnię w jednostce czasu, a kierunek wskazuje kierunek przenoszenia tej energii. Pamiętając, że wektory <math>\overrightarrow{E}\,</math> i <math>\overrightarrow{B}\,</math> są do siebie prostopadłe zapisujemy wzór w postaci wektorowej: <math>\overrightarrow{P}=\frac{1}{\mu_0}\overrightarrow{E}\times \overrightarrow{B}</math>. Określony tym wzorem wektor nosi nazwę wektora Poyntinga. | ||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="450px" valign="top"|[[Grafika:PF1_M15_Slajd16.png]] | |||
|valign="top"|'''Optyka geometryczna''' | |||
Rozchodzenie się światła, podobnie jak i fal elektromagnetycznych o innych długościach, polega na przemieszczaniu się w czasie i przestrzeni drgań wektorów natężeń pól: elektrycznego i magnetycznego. Prędkość światła w próżni oznaczyliśmy symbolem <math>c\,</math>. Jak stwierdziliśmy, w innych ośrodkach prędkość ta jest mniejsza, co wynika z równań Maxwella, i zależy od względnej przenikalności elektrycznej <math>\varepsilon\,</math> i magnetycznej <math>\mu\,</math> ośrodka. Współczynnik załamania światła w ośrodku definiujemy wzorem <math>n=\frac{c}{v}</math>, a więc prędkość światła w danym ośrodku można wyrazić następująco: <math>n=\sqrt{\varepsilon \mu}\approx \sqrt{\varepsilon}</math>. Przybliżona równość w tym wzorze wynika z faktu, że dla większości ośrodków, w których rozważamy rozchodzenie się światła, wartość przenikalności magnetycznej jest na tyle bliska jedności, że można ją tu pominąć. Otrzymujemy w ten sposób wynikającą z równań Maxwella interesującą zależność między współczynnikiem załamania i przenikalnością elektryczną dla większości (nie ferromagnetycznych) ośrodków <math>n\approx \sqrt{\varepsilon}</math>. Dodajmy do tego jeszcze, że chociaż w falach elektromagnetycznych mamy do czynienia z drganiami wektorów <math>\overrightarrow{E}\,</math> i <math>\overrightarrow{B}\,</math>, to doświadczalnie stwierdzono decydującą rolę drgań pola elektrycznego dla reakcji fotochemicznych, fotoelektrycznych czy również fizjologicznych. Dlatego w rozważaniach naszych będziemy mówić o drganiach wektora natężenia pola elektrycznego jako o drganiach wektora świetlnego. Stosunek prędkości światła w próżni do prędkości światła w danym ośrodku oznaczyliśmy symbolem <math>n\,</math> i nazywamy współczynnikiem załamania. Często nazywa się go także bezwzględnym współczynnikiem załamania, gdyż określa załamanie światła przy przejściu z próżni do ośrodka. Jeśli światło przechodzi z ośrodka <math>1\,</math>, gdzie rozchodzi się z prędkością <math>v_1\,</math> do ośrodka <math>2\,</math>, gdzie prędkość światła wynosi <math>v_2\,</math>, załamanie jest określone przez współczynnik załamania ośrodka drugiego względem ośrodka pierwszego <math>n_{2,1}=\frac{n_2}{n_1}=\frac{v_1}{v_2}</math>. | |||
Wersja z 11:07, 17 sie 2006

|

|
Nasze rozważania rozpoczniemy od przypomnienia równań Maxwella, które przedstawiają relacje pomiędzy zmianami pól: elektrycznego i magnetycznego w czasie i przestrzeni. |

|
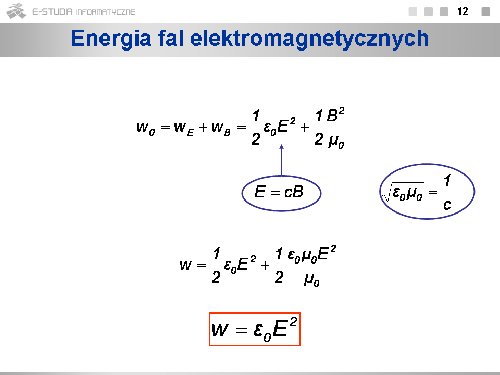
Możemy też gęstość energii fali elektromagnetycznej przedstawić w postaci: lub . |