PF Moduł 15: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 126: | Linia 126: | ||
|width="450px" valign="top"|[[Grafika:PF1_M15_Slajd14.png]] | |width="450px" valign="top"|[[Grafika:PF1_M15_Slajd14.png]] | ||
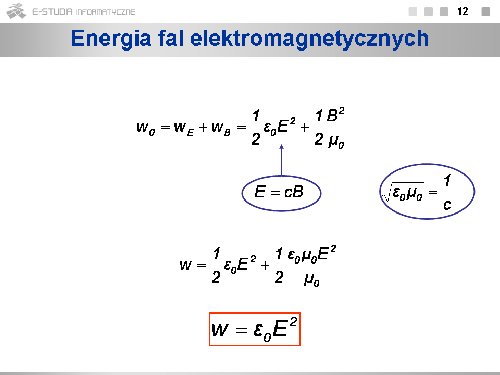
|valign="top"|Określmy teraz energię transportowaną przez falę elektromagnetyczną w próżni w jednostce czasu. Kierunek transportu energii pokrywa się z kierunkiem rozchodzenia się fali i jest prostopadły do kierunków wektorów <math>\overrightarrow{E}\,</math> i <math>\overrightarrow{B}\,</math>. W czasie <math>dt\,</math> fala przesuwa się o odcinek <math>c\dot dt\,</math>. Przez powierzchnię <math>S\,</math> prostopadłą do kierunku rozchodzenia się fali przetransportowana jest energia zawarta w objętości <math>S\cdot c \cdot dt\,</math>. Energia ta wynosi: <math>dW=wdV\,</math> Energia przenoszona przez jednostkową powierzchnię <math>w\,</math> jednostce czasu wynosi więc: <math>P=\frac{1}{S}\frac{dW}{dt}=\varepsilon_0 cE^2</math> | |valign="top"|Określmy teraz energię transportowaną przez falę elektromagnetyczną w próżni w jednostce czasu. Kierunek transportu energii pokrywa się z kierunkiem rozchodzenia się fali i jest prostopadły do kierunków wektorów <math>\overrightarrow{E}\,</math> i <math>\overrightarrow{B}\,</math>. W czasie <math>dt\,</math> fala przesuwa się o odcinek <math>c\dot dt\,</math>. Przez powierzchnię <math>S\,</math> prostopadłą do kierunku rozchodzenia się fali przetransportowana jest energia zawarta w objętości <math>S\cdot c \cdot dt\,</math>. Energia ta wynosi: <math>dW=wdV\,</math> Energia przenoszona przez jednostkową powierzchnię <math>w\,</math> jednostce czasu wynosi więc: <math>P=\frac{1}{S}\frac{dW}{dt}=\varepsilon_0 cE^2</math> | ||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="450px" valign="top"|[[Grafika:PF1_M15_Slajd15.png]] | |||
|valign="top"|Wykorzystując związki: <math>E=cB</math> oraz <math>c=\frac{1}{\sqrt{\varepsilon_0 \mu_0}}</math> możemy wzór na energię przenoszona przez jednostkową powierzchnię w jednostce czasu przedstawić jako: <math>P=\frac{EB}{\mu_0}</math>. Ponieważ, jak to już stwierdziliśmy, energia ta przenoszona jest w kierunku prostopadłym do wektorów <math>\overrightarrow{E}\,</math> i <math>\overrightarrow{B}\,</math>, możemy zdefiniować wektor, którego wartość określa energię przenoszoną przez jednostkową powierzchnię w jednostce czasu, a kierunek wskazuje kierunek przenoszenia tej energii. Pamiętając, że wektory <math>\overrightarrow{E}\,</math> i <math>\overrightarrow{B}\,</math> są do siebie prostopadłe zapisujemy wzór w postaci wektorowej: <math>\overrightarrow{P}=\frac{1}{\mu_0}\overrightarrow{E}\times \overrightarrow{B}</math>. Określony tym wzorem wektor nosi nazwę wektora Poyntinga. | |||
Wersja z 10:56, 17 sie 2006

|

|
Nasze rozważania rozpoczniemy od przypomnienia równań Maxwella, które przedstawiają relacje pomiędzy zmianami pól: elektrycznego i magnetycznego w czasie i przestrzeni. |

|
Możemy też gęstość energii fali elektromagnetycznej przedstawić w postaci: lub . |