PF Moduł 15: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 110: | Linia 110: | ||
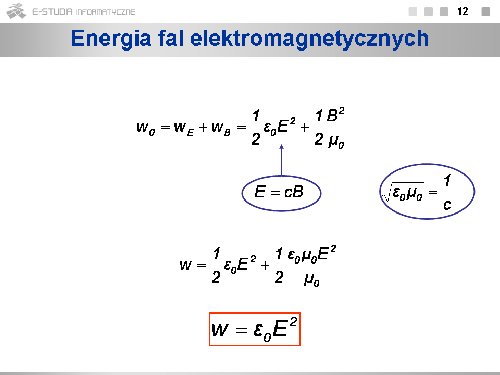
Jeśli fala elektromagnetyczna jest w stanie pobudzić do działania telewizor, czy telefon komórkowy, to musi przenosić energię z jednego miejsca przestrzeni do drugiego. Skorzystajmy ze wzorów na gęstość energii pola elektrycznego oraz na gęstość energii pola magnetycznego. Gęstość energii, to energia przypadająca na jednostkę objętości. Całkowita energia fali elektromagnetycznej zmagazynowana w jednostce objętości jest sumą energii pola elektrycznego i pola magnetycznego. Po uwzględnieniu związku między wartościami <math>E\,</math> i <math>B\,</math> dla fali elektromagnetycznej <math>E=cB\,</math>, otrzymujemy wzór na gęstość energii fali: <math>w=\varepsilon_0 E^2</math>. | Jeśli fala elektromagnetyczna jest w stanie pobudzić do działania telewizor, czy telefon komórkowy, to musi przenosić energię z jednego miejsca przestrzeni do drugiego. Skorzystajmy ze wzorów na gęstość energii pola elektrycznego oraz na gęstość energii pola magnetycznego. Gęstość energii, to energia przypadająca na jednostkę objętości. Całkowita energia fali elektromagnetycznej zmagazynowana w jednostce objętości jest sumą energii pola elektrycznego i pola magnetycznego. Po uwzględnieniu związku między wartościami <math>E\,</math> i <math>B\,</math> dla fali elektromagnetycznej <math>E=cB\,</math>, otrzymujemy wzór na gęstość energii fali: <math>w=\varepsilon_0 E^2</math>. | ||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="450px" valign="top"|[[Grafika:PF1_M15_Slajd13.png]] | |||
|valign="top"|Możemy też gęstość energii fali elektromagnetycznej przedstawić w postaci: <math>w=\frac{B^2}{\mu_0}</math> lub <math>w=\sqrt{\frac{\varepsilon_0}{\mu_0}}\cdot EB</math>. | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="450px" valign="top"|[[Grafika:PF1_M15_Slajd14.png]] | |||
|valign="top"|Określmy teraz energię transportowaną przez falę elektromagnetyczną w próżni w jednostce czasu. Kierunek transportu energii pokrywa się z kierunkiem rozchodzenia się fali i jest prostopadły do kierunków wektorów <math>\overrightarrow{E}\,</math> i <math>\overrightarrow{B}\,</math>. W czasie <math>dt\,</math> fala przesuwa się o odcinek <math>c\dot dt\,</math>. Przez powierzchnię <math>S\,</math> prostopadłą do kierunku rozchodzenia się fali przetransportowana jest energia zawarta w objętości <math>S\cdot c \cdot dt\,</math>. Energia ta wynosi: <math>dW=wdV\,</math> Energia przenoszona przez jednostkową powierzchnię <math>w\,</math> jednostce czasu wynosi więc: <math>P=\frac{1}{S}\frac{dW}{dt}=\varepsilon_0 cE^2</math> | |||
Wersja z 10:45, 17 sie 2006

|

|
Nasze rozważania rozpoczniemy od przypomnienia równań Maxwella, które przedstawiają relacje pomiędzy zmianami pól: elektrycznego i magnetycznego w czasie i przestrzeni. |

|
Możemy też gęstość energii fali elektromagnetycznej przedstawić w postaci: lub . |