PF Moduł 15: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 4: | Linia 4: | ||
|} | |} | ||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="450px" valign="top"|[[Grafika:PF1_M15_Slajd2.png]] | |||
|valign="top"|'''Wstęp''' | |||
Równania Maxwella w elegancki sposób opisują wszystkie zjawiska dotyczące pola elektrycznego i magnetycznego. Można z nich wyprowadzić znane dawniej prawa empiryczne takie, jak prawo Faradaya czy prawo Ampera. Ale równania Maxwella zawierają jeszcze więcej informacji. Po odpowiednim ich przekształceniu otrzymujemy równanie falowe, a prędkość opisywanej przez nie fali równa jest prędkości światła w próżni. Światło jest więc falą elektromagnetyczną. W tym wykładzie dowiemy się, jakie są jeszcze inne rodzaje fal elektromagnetycznych. Telefony komórkowe, radio, telewizja, łączność satelitarna, nawigacja morska i lotnicza, systemy radiolokacji - wszystko to opiera się na czterech równaniach Maxwella. O elektromagnetycznej naturze światła wiemy od czasów Maxwella, czyli końca XIX wieku. Ale już dwa wieki wcześniej opisywano światło jako falę. Sformułowane przez Pierre'a Fermata w 1650 roku i Christiana Huyghensa w 1678 roku zasady stanowią podstawę optyki geometrycznej. Pokażemy, jak podstawowe prawa optyki: prawo odbicia i załamania światła można uzyskać z tych zasad. | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="450px" valign="top"|[[Grafika:PF1_M15_Slajd3.png]] | |||
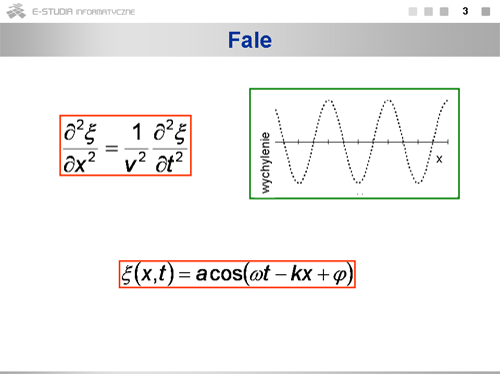
|valign="top"|'''Propagacja fal elektromagnetycznych''' | |||
Przypomnijmy sobie podstawowe fakty o propagacji fal. Fala to rozchodzenie się w ośrodku drgań cząsteczek. Wychylenie <math>\xi\,</math> z położenia równowagi cząstek biorących udział w ruchu falowym, opisuje wzór: <math>\xi (x,t)=acos(\omega t-kx+\varphi)</math>, gdzie <math>k=\frac{2\pi}{\lambda}</math> jest liczbą falową, <math>\omega=\frac{2\pi}{T}</math> częstością, a <math>\varphi\,</math> - fazą początkową. Funkcja <math>\xi (x,t)=acos(\omega t-kx+\varphi)</math> jest rozwiązaniem równania falowego: | |||
: <math>\frac{\partial^2 \xi}{\partial x^2}=\frac{1}{v^2}\frac{\partial^2 \xi}{\partial t^2}</math>. | |||
|} | |||
<hr width="100%"> | |||
Wersja z 09:21, 17 sie 2006

|