Laboratorium wirtualne 1/Moduł 5 - ćwiczenie 5

---

---

Tradycyjna analiza widmowa Fouriera jako superpozycja funkcji sinus i cosinus jest niemal wszechobecna w dziedzinie identyfikacji i analizy sygnałów pomiarowych. Użyteczność transformaty Fouriera zawiera się w jej zdolności do analizy przebiegu czasowego sygnału pod kątem jego „zawartości częstotliwościowej”. Należy podkreślić, że tradycyjna analiza częstotliwościowa nie nadaje się do obserwacji właściwości sygnałów niestacjonarnych. Wymagana jest tutaj analiza wykorzystująca łączne czasowo-częstotliwościowe (t/f) reprezentacje sygnałów (JFTA - Joint Time-Frequency Analysis). Tego rodzaju analizę zapewnia krótkoczasowa transformata Fouriera, czy też transformata Gabora. Rodzajem analizy czasowo-częstotliwościowej jest również transformacja falkowa. Najbardziej charakterystyczne dla transformaty falkowej jest to, że indywidualne funkcje falkowe są dobrze zlokalizowane w czasie (lub przestrzeni – dla obrazów) i jednocześnie dobrze opisują sygnał w dziedzinie częstotliwości, ściśle biorąc tzw. skali. Ponadto w odróżnieniu od funkcji sinus i cosinus, które definiują unikalną transformatę Fouriera, nie ma pojedynczego, unikalnego zbioru falkowych funkcji bazowych. Falki różnią się między sobą zwartością lokalizacji czasowej oraz płynnością i gładkością kształtów. Wynikająca stąd zdolność falek do opisu sygnałów „z nieciągłościami”, przy ograniczonej liczbie współczynników oraz z lokalizacją w czasie, stanowi o jej przewadze nad transformatą Fouriera.

---

Krótkoczasowa transformata Fouriera (STFT – Short-Time Fourier Transform) stanowi wzorcowy przykład algorytmu analizy czasowo-częstotliwościowej. Umożliwia ona wydobycie z sygnału informacji o tym, jak zmienia się jego widmo w czasie, czyli jednoczesną obserwację jego właściwości zarówno w dziedzinie czasu jak i częstotliwości. Wycinek sygnału (blok próbek o rozmiarze L) przeznaczony do analizy jest sukcesywnie dzielony na segmenty, z których każdy podlega analizie widmowej niezależnie. Podobnie jak w przypadku tradycyjnym, aby usunąć gwałtowne zmiany (cięcia) sygnału na krańcach przedziałów, stosuje się różne okna czasowe w odniesieniu do wspomnianych segmentów. Przesuwając okno w czasie, wzdłuż sygnału, wyznacza się jego zawartość widmową wewnątrz przedziału czasowego, którego długość jest określona szerokością okna. Krótkoczasową transformatę Fouriera sygnału $x(t)$, w odniesieniu do okna $\phi (t)$ rozmieszczonego w pozycji $(\tau ,\xi )$ na płaszczyźnie t/f zdefiniować można jako (1). W odróżnieniu od tradycyjnej transformaty Fouriera, dla której do wyznaczenia pojedynczej składowej konieczna jest znajomość funkcji $x(t)$ na całej osi czasu, w tym przypadku, wymagana jest znajomość $x(t)$ tylko w przedziale określonym przez położenie $\phi (t-\tau )$. Dyskretna wersja powyższego równania przyjmuje postać: $X({\tau }_n,{\xi }_k)=T_p\sum _{i=0}^{N-1}x(t_i)\phi (t_i-{\tau }_n)e^{-j{\xi }_k{t}_i}$ gdzie $T_p$ oznacza okres próbkowania sygnału. Dla przypadku unormowanego, gdy $T_p=1$ otrzymujemy zależność (2).

---

Kształt okna czasowego $\phi (t)$ rozmieszczonego w pozycji $(\tau ,\xi )$ na płaszczyźnie t/f odgrywa kluczową rolę w przypadku STFT. Iloczyn szerokości okna w dziedzinie czasu ${\mathrm{\Delta }}_t$ i szerokości okna w dziedzinie częstotliwości ${\mathrm{\Delta }}_{\omega }$ jest wielkością stałą dla danego okna. Stąd też, poprawiając rozdzielczość w dziedzinie czasu, będziemy ją pogarszać w dziedzinie częstotliwości i odwrotnie. Zatem szerokość okna wybierana jest na drodze kompromisu. Interpretacja położenia okna czasowo-częstotliwościowego na płaszczyźnie t/f przedstawiona jest na rysunku 1.

---

Na rysunku 2 pokazany jest przykład zastosowania rozkładu STFT do sygnału o postaci: $x(t)=sin2\pi f_{1}t+sin2\pi f_{2}t+\alpha [\delta (t-t_1)+\delta (t-t_2)]$ dla różnych szerokości (promieni) ${\mathrm{\Delta }}_t$ okna czasowego $\phi (t)$. W przypadku zastosowania szerokiego okna czasowego, otrzymuje się bardzo dużą rozdzielczość częstotliwościową i bardzo małą rozdzielczość czasową. W miarę zwężania okna czasowego poprawia się rozdzielczość czasowa kosztem częstotliwościowej.

---

Znany jest pewien przypadek szczególny, w którym okno czasowe ma kształt gaussowski opisany wzorem (3). Okazuje się, że widmo tego okna ma również kształt gaussowski: $\mathrm{\Phi }(\omega )=G_{\alpha }(\omega )=e^{-\alpha {\omega }^2},\alpha >0$ Okno to, od nazwiska pierwszego użytkownika, nosi miano okna Gabora. Iloczyn szerokości okna Gabora w dziedzinie czasu ${\mathrm{\Delta }}_t$ i szerokości okna w dziedzinie częstotliwości ${\mathrm{\Delta }}_{\omega }$ osiąga minimum i wynosi: ${\mathrm{\Delta }}_t{\mathrm{\Delta }}_{\omega }=\frac{1}{2}$ Analityczny zapis transformaty Gabora przedstawia zależność (4). Inaczej: $G(\tau ,\xi )=⟨x(t),g_{\alpha }(t-\tau )e^{j\xi t}⟩$ Do celów obliczeń numerycznych wprowadza się pojęcie dyskretnej transformaty Gabora, określanej w skończonym zbiorze punktów na płaszczyźnie t/f. Zdyskretyzowana wersja transformaty (w sensie położenia okna na płaszczyźnie t/f) jest opisana następującą zależnością: Parser nie mógł rozpoznać (błąd składni): {\displaystyle G(\tau_n, \xi_k)=\int_{-\infty}^{+\infty} {x(t){g_{\alpha}^{*}(t-\tau_n)e^{-j\xi_k t}}\, dt}

---

Praktyczny algorytm obliczeniowy dyskretnego rozkładu Gabora ma postać określoną wzorem (5). Współczynniki rozkładu Gabora są wyznaczane za pomocą algorytmu STFT z równania (6) gdzie $N$ oznacza liczbę przedziałów częstotliwości, $T_p$ okres próbkowania, $\gamma [n]$ funkcję dualną do $g_{\alpha }[n]$.

---

Rysunek 3 przedstawia panel czołowy wirtualnego przyrządu pomiarowego JTFA (Joint Time-Frequency Analyser) skonstruowanego przez autorów. Przyrząd ten jest udostępniony w sieci jako aplet poprzez dowolną przeglądarkę WWW Przyrząd JTFA może być wykorzystywany do analizy czasowo-częstotliwościowej dowolnych sygnałów jednowymiarowych zapisanych uprzednio w plikach. Istnieje też możliwość wczytania sygnału przy pomocy karty zbierania danych zainstalowanej w komputerze. Jeśli używamy karty zbierania danych musimy określić parametry związane z pobraniem sygnału. W szczególności są to parametry sygnału: częstotliwość próbkowania (Sampling Rate) i ilość próbek (# of Samples) oraz parametry związane z kartą: numer kanału (Channel), z którego odczytujemy dane i wzmocnienie w kanale (Gain). Po wybraniu opcji ACQ SIGNAL nastąpi pobranie sygnału. Zakres częstotliwości analizy jest zawarty w przedziale od składowej stałej do częstotliwości Nyquista, tj. połowy częstotliwości próbkowania. Najwyższa możliwa do uzyskania częstotliwość próbkowania zależy od użytej karty zbierania danych i od możliwości komputera. Częstotliwość próbkowania nie wpływa na wyniki obliczeń, ale jest odzwierciedlana jako oś y widma mocy i spektrogramu. Sygnał wczytany poprzez kartę można zapisać w pliku w celu późniejszego jego wykorzystania (opcja SAVE). Z kolei wybranie polecenia READ FILE umożliwia wczytanie sygnału zapisanego w pliku. Dane w pliku powinny mieć format wektora kolumnowego liczb (znaki ASCII). Nazwa wczytanego pliku jest zawsze widoczna w polu File Name. Wirtualny przyrząd pomiarowy JTFA wykorzystuje następujące pola wyświetlania danych (rys.3): wyświetlacz widmo mocy / widmo chwilowe (power spectrum / instantenous spectrum) pokazuje klasyczne widmo mocy albo widmo chwilowe w zależności od ustawień, wyświetlacz spektrogramu pokazuje widmo w skali czasu dla wybranej metody analizy; wartości widma są w tym przypadku symbolizowane przy użyciu kolorów, wyświetlacz sygnału analizowanego w czasie. Sposób wyświetlania danych można zmienić przez przestawienie przełącznika Linear/dB i/lub Cursor. Przełączenie Linear/dB zmienia sposób prezentowania spektrogramu ze skali liniowej na decybelową i odwrotnie. Przełącznik Cursor włącza lub wyłącza wyświetlanie kursorów. Jeśli kursory są włączone wyświetlacz widma mocy zamienia się w wyświetlacz widma chwilowego. Widmo chwilowe jest liczone dla czasu wskazywanego przez kursor (oś x). Do trybu wyświetlania widma mocy można w dowolnej chwili powrócić wciskając przycisk Power Spectrum. W opisywanym przyrządzie wirtualnym do analizy czasowo-częstotliwościowej sygnału jednowymiarowego można wykorzystać jeden z algorytmów: krótkoczasową transformatę Fouriera (STFT) transformację Gabora i inne Najprostszą z tych metod jest STFT (Short Time Fourier Transform). Przed jej użyciem należy określić okno analizy (Window Type) oraz długość okna (Window Length), tak aby uzyskać najlepszy kompromis pomiędzy rozdzielczością w czasie i częstotliwości. Można wybrać okna: prostokątne, Hanninga, Hamminga, Blackmana-Harris’a, Blackmana. Jeśli wydłużamy okno uzyskujemy lepszą rozdzielczość w częstotliwości, ale rozdzielczość w czasie staje się gorsza i na odwrót. Transformacja Gabora jest bardziej skomplikowana obliczeniowo, ale w wyniku uzyskujemy lepszą rozdzielczość czasowo-częstotliwościową. Przed wybraniem tej metody musimy podać wartości: Order, Var i Window Length. Oknem stosowanym w metodzie Gabora jest optymalne okno Gaussa opisane przez podanie długości (Length) i wariancji (Var). Wartość rządu (Order) określa rozdzielczość, ale jednocześnie poziom niepożądanych interferencji pomiędzy elementami analizowanego sygnału. Im wyższy jest rząd tym lepsza jest rozdzielczość czasowo-częstotliwościowa. Jednocześnie ze zwiększaniem rzędu coraz bardziej widoczne są pasożytnicze interferencje. Także czas obliczeń jest proporcjonalny do rzędu. Zwykle wybranie rzędu na poziomie trzy do pięciu daje najlepszy kompromis pomiędzy rozdzielczością i zawartością pasożytniczych interferencji. Pewną eliminację pasożytniczych interferencji można również uzyskać zmniejszając wariancję okna Gaussa (Var), ale jednocześnie ulega pogorszeniu rozdzielczość czasowo-częstotliwościowa.

---

Na rysunku 4 pokazane są wyniki analizy STFT otrzymane przy wykorzystaniu opisywanego wyżej wirtualnego przyrządu pomiarowego do przeprowadzania analiz czasowo-częstotliwościowych. Sygnał badany, spróbkowany z częstotliwością 500Hz, składa się z dwóch części wyciętych oknami Gaussa (przedziały czasowe $0.08÷0.15sek.$ i $0.25÷0.58sek.$). Część pierwszą stanowi sygnał sinusoidalny o częstotliwości 156Hz, część druga to złożenie dwóch sygnałów: sinusoidalnego o częstotliwości 50Hz oraz sinusoidalnego o częstotliwości liniowo zmiennej w zakresie $90÷240Hz$. Na dole rysunku 11 pokazany jest przebieg czasowy tego sygnału. Po środku przedstawiony jest obraz widma mocy badanego sygnału. Z widma mocy można wywnioskować, jakie składowe częstotliwościowe występują w sygnale badanym, ale nic nie można powiedzieć o chwilach czasu występowania składowych sygnału związanego z tymi częstotliwościowymi. Równie trudno jest określić charakter zmian częstotliwościowych. Natomiast obserwując rozkład na płaszczyźnie t/f, możemy podać zarówno czas występowania składowych sygnału o określonej zawartości częstotliwościowej, jak i charakter zmian częstotliwościowych. Niestety wartości czasu i częstotliwości można określić tylko z pewnym prawdopodobieństwem wyznaczonym przez parametry okna. Zastosowanie wąskiego okna czasowego (i tym samym szerokiego w dziedzinie częstotliwości) objawia się dużym rozmyciem umiejscowienia prążków w dziedzinie częstotliwości i stosunkowo dobrym umiejscowieniem prążków w czasie (rysunek z prawej). Zastosowanie szerokiego okna czasowego (rysunek z lewej) daje dobrą lokalizację częstotliwościową i złą czasową.

---

Na rysunku 5 pokazano wyniki analizy czasowo-częstotliwościowej opisanego poprzednio sygnału, przeprowadzonej tym razem z użyciem transformaty Gabora. Zastosowanie okna Gabora umożliwia osiągnięcie optymalnych rozdzielczości zarówno w dziedzinie czasu, jak i częstotliwości.

---

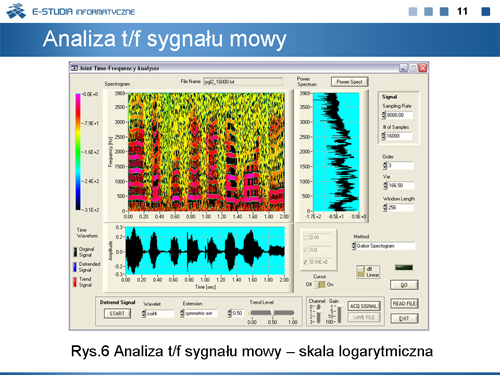
Na rysunku 6 zaprezentowany jest przykład użycia analizy czasowo-częstotliwościowej do sygnału mowy. Obserwacja spektrogramu pozwala zilustrować mechanizm mowy ludzkiej. Rysunek u góry (część górna lewa) obrazuje energię sygnału jako funkcję czasu i częstotliwości. Można z niego łatwo odczytać, jakie składowe częstotliwościowe występują w poszczególnych dźwiękach. Odpowiadające częstotliwościom kolory odzwierciedlają intensywności poszczególnych składowych. Rysunek u góry po prawej to widmo mocy przetwarzanego sygnału. Od razu widać, że niesie ono dużo mniej informacji niż spektrogram. Spektrogram wykreślony w skali logarytmicznej lepiej obrazuje duże różnice amplitud poszczególnych składowych częstotliwościowych.

---

Innym zastosowaniem analizy czasowo-częstotliwościowej jest detekcja mocno zaszumionych sygnałów. W ogólności szumy równomiernie rozprzestrzeniają energię zarówno w dziedzinie czasu jak i częstotliwości. Sygnały użyteczne z kolei, często koncentrują swoją energię w relatywnie krótkich zakresach czasowych, albo wąskich zakresach częstotliwościowych. Konwersja zaszumionego sygnału do domeny czas-częstotliwość zwykle znacząco poprawia lokalną wartość współczynnika SNR (Signal-to-Noise-Ratio). Rysunek 7 przedstawia zaszumiony sygnał o częstotliwości zmiennej wykładniczo. Szumy dominują zarówno w przebiegu czasowym, jak i widmie mocy. Analizując te przebiegi praktycznie niemożliwe jest wykrycie właściwego sygnału. Jednak po przejściu do dziedziny czas-częstotliwość od razu można go wykryć, oraz podać zarówno umiejscowienie w czasie jak i charakter zmian częstotliwości. Co więcej bazując na reprezentacji czasowo-częstotliwościowej danego sygnału można zamaskować współczynniki związane z szumem i, korzystając z transformacji odwrotnej, odtworzyć postać sygnału bez szumu.

---