CWGIĆwiczenie 2

Ćwiczenia 2. Elementy wspólne i przynależne w odwzorowaniach przestrzennych Zadanie2.1. Wyznaczyć krawędź przecięcia się dwu płaszczyzn określonych śladami a i b Krawędź przecięcia się płaszczyzn równoległych do osi $x$ jest prostą również równoległą do osi $x$. W celu wyznaczenia rzutów krawędzi niezbędne jest przeprowadzenie operacji pozwalających określić usytuowanie tych rzutów względem osi x. W tym celu, oprócz rzutni pionowej i poziomej, wprowadzamy dodatkową rzutnię boczną, prostopadłą do tych dwóch. Wyznaczamy trzecie rzuty płaszczyzn $\alpha$ i $\beta$. W tym rzucie płaszczyzny przyjmą postać rzutujących, a więc otrzymamy trzecie rzuty śladów płaszczyzn będących jednocześnie ich rzutami. Trzecie rzuty płaszczyzn (ślady płaszczyzn) przecinają się w punkcie $k^{‴}$, który będzie jednocześnie trzecim rzutem krawędzi. Powracając do układu dwóch rzutni, pionowej i poziomej otrzymamy poszukiwane rzuty krawędzi przecięcia się płaszczyzn $k^{\prime }$, $k^{″}$.

---

Zadanie 2.2. Wyznaczyć punkt przebicia prostej $m$ z pasem płaszczyzny zawartym między prostymi $\alpha (a||b)$ Rozwiązując zadanie musimy się zastanowić nad trybem postępowania. W tym przypadku powinniśmy postąpić w sposób następujący: przez prostą $m$ poprowadzić dowolną płaszczyznę $\beta$, najwygodniej rzutująca (pionowo-zutującą,) wyznaczyć krawędź $k$, przecięcia się płaszczyzny $\beta$ z płaszczyzna $\alpha (a||b)$, punkt, w którym krawędź $k$ przetnie daną prostą $m$ jest poszukiwanym punktem $P$, przebicia prostej $m$ z płaszczyzną $\alpha$ Jak widać z przedstawionego schematu postępowania punkty należące do krawędzi $k$ będą należały jednocześnie do płaszczyzn $\alpha$ i $\beta$. Zatem punkt przecięcia się prostej $m$ z krawędzią $k$ będzie punktem wspólnym prostej $m$ i płaszczyzny $\alpha$ (będzie punktem przebicia płaszczyzny $\alpha (a||b)$ przez prostą $m$ - rys. C2.2b). Dla wygody dalszego postępowania poprowadźmy przez prostą $m$ płaszczyznę pionowo-rzutujacą $\beta$. Ponieważ płaszczyzna $\beta$ jest rzutująca, to wszystkie elementy płaskie znajdujące się w tej płaszczyźnie w rzucie pionowym będą leżały na rzucie pionowym płaszczyzny $\beta$ (ślad pionowy płaszczyzny $v_{\beta }$ będzie pokrywał się z rzutem płaszczyzny $\beta$). Zatem rzut pionowy krawędzi $k^{″}$, przecięcia się płaszczyzn $\alpha$ i $\beta$ będzie również pokrywał się z rzutem pionowym płaszczyzny $\beta$. Krawędź $k$ należy również do płaszczyzny $\alpha$, a więc rzut pionowy krawędzi $k^{″}$ przecina proste $a^{″}$ i $b^{″}$, tworzące tą płaszczyznę, odpowiednio w punktach $1^{″}$ i $2^{″}$. Rzuty poziome tych punktów wyznaczymy na rzutach poziomych prostych $a$ i $b$. Następnie znajdujemy punkt przecięcia się wyznaczonej krawędzi z prostą $m$. W rzucie pionowym obie proste pokrywają się, więc wyznaczenie tego punktu jest niemożliwe, natomiast w rzucie poziomym bez trudu wyznaczymy rzut poziomy $P^{\prime }$ poszukiwanego punktu przebicia $P$. Na odnoszącej i rzutach pionowych prostych $k$ i $m$ będzie znajdował się rzut pionowy punktu przebicia $P^{″}$. Do pełnego rozwiązania zadania niezbędne jest ustalenie widoczności prostej $m$, przy założeniu, że pas między prostymi $a$ i $b$ jest nieprzezroczysty. W tym celu w miejscu przecięcia się rzutów prostej $m$ z prostą należącą do płaszczyzny $\alpha$ ( np. $a$) obieramy punkty i analizujemy, które z nich mają większą głębokość (dla rzutów pionowych) względnie wysokość (dla rzutów poziomych). Np. analizując punkty: punkt $2^{″}$, należący do prostej $m$ oraz punkt $3^{″}$ należący do prostej $b$, widzimy w rzucie poziomym, że punkt $3$ ma większą głębokość, a więc prosta $m$ w tym punkcie, w rzucie pionowym jest widoczna, prosta $b$ jest niewidoczna, co oznaczamy linią kreskową aż do punktu przebicia $P^{″}$. Analogiczne postępowanie przeprowadzamy dla punktów $4^{\prime }$ i $5^{\prime }$, należących do prostych $a$ i $m$.

---

Zadanie 2.3. Wyznaczyć linię przenikania dwóch figur płaskich, trójkąta $PQR$ z równoległobokiem $ABCD$. Przyjmując, że płaszczyzny figur są nieprzezroczyste ustalić ich widoczność. Linia przenikania figur płaskich to nic innego jak odcinek krawędzi przecięcia się płaszczyzn, zdefiniowanych przez te figury, wspólny dla obu płaszczyzn. Należy, zatem wyznaczyć wspólną krawędź przecięcia się płaszczyzn reprezentowanych przez trójkąt i równoległobok. Krawędź wyznaczymy metodą pośrednią, poszukując punktów przebicia bokiem jednej z figur płaszczyzny drugiej figury. Wyznaczenie dwóch punktów przebicia, czyli dwóch punktów wspólnych tych płaszczyzn określi nam krawędź przecięcia się płaszczyzn (dwa punkty, jednoznacznie, określają prostą). 1). Wyznaczmy punkt przebicia boku $CD$ równoległoboku z płaszczyzną trójkąta $PQR$. W tym celu poprowadzimy płaszczyznę pionowo - rzutującą $\alpha$ przez bok $CD$ równoległoboku. Płaszczyzna jest rzutująca, a więc krawędź przecięcia się tej płaszczyzny z płaszczyzną równoległoboku $k_1$ będzie leżała w płaszczyźnie $\alpha$, ale również w płaszczyźnie trójkąta. Rzut pionowy tej krawędzi będzie pokrywał się z rzutem pionowym płaszczyzny $\alpha$ oraz z rzutem pionowym boku $C^{″}{D}^{″}$. Przynależność krawędzi $k_1$ do płaszczyzny trójkąta oznacza, że punkty $1^{″}$ i $2^{″}$ są rzutami punktów przecięcia się krawędzi z rzutami boków $P^{″}{Q}^{″}$ oraz $R^{″}{Q}^{″}$. Rzuty poziome tych punktów znajdziemy na przecięciu się odnoszących prostopadłych do osi $x$ z rzutami poziomymi boków trójkąta $P^{\prime }{Q}^{\prime }$ oraz $R^{\prime }{Q}^{\prime }$. W ten sposób znajdujemy rzuty krawędzi $k_1{\text{'}}^{\prime }$ oraz $k_1\text{'}$. W rzucie poziomym otrzymamy szukany punkt przebicia $II\text{'}$ boku $C^{\prime }{D}^{\prime }$ równoległoboku z płaszczyzną trójkąta. Rzut pionowy tego punktu wyznaczymy jako przecięcie odnoszącej z rzutem pionowym krawędzi $k_1{\text{'}}^{\prime }$ (oraz boku $C^{″}{D}^{″}$). 2). Podobną konstrukcję przeprowadzamy z inną parą np.: boku trójkąta oraz płaszczyzny równoległoboku $ABCD$. Wybierzmy do rozważań bok $RQ$ trójkąta, przez który poprowadzimy płaszczyznę $\beta$ a następnie, w drodze postępowania analogicznego jak poprzednio, wyznaczymy krawędź przecięcia się płaszczyzny $\beta$ z płaszczyzną równoległoboku oraz w konsekwencji punkt przebicia $III$ boku $QR$ z równoległobokiem $ABCD$. Podobnie jak w poprzednim zadaniu ustalamy widoczność poszczególnych krawędzi analizując odpowiednio wysokość i głębokość punktów znajdujących się na przecięciu się rzutów poszczególnych boków figur płaskich. Dla rzutu pionowego analizujemy głębokości punktów 2 i 3, dla rzutu poziomego – wysokości punktów 7 i 8. Po analizie oznaczamy krawędzie i płaszczyzny widoczne oraz niewidoczne.

---

Zadanie 2.3. Wyznaczyć punkty przebicia ostrosłupa ABCW prostą n. Ustalmy tok postępowania przy rozwiązaniu tego zadania: przez dowolny punkt $1$ leżący na prostej $n$ oraz wierzchołek $W$ ostrosłupa poprowadźmy prostą $a$, dwie proste przecinające się $a$ i $n$ określają płaszczyznę $\alpha$. Wyznaczamy przekrój ostrosłupa płaszczyzną $\alpha$, w punktach przecięcia się boków wielokąta przekroju z prostą $n$ wyznaczymy poszukiwane punkty przebicia ścian ostrosłupa z prostą $n$. 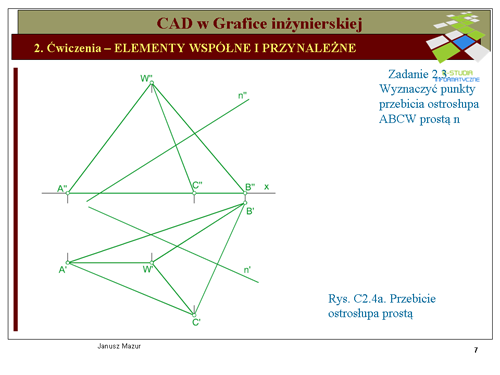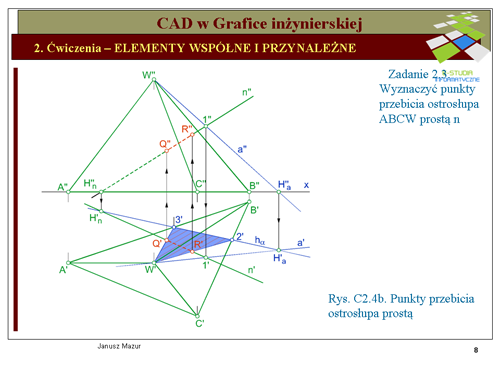Obierając punkt $1$ na prostej $n$ oraz prowadząc prostą $a$ przez punkt $1$ i wierzchołek $W$ ostrosłupa wyznaczamy przekrój ostrosłupa płaszczyzną określoną przez te proste. Wierzchołek W będzie stanowił jeden z wierzchołków figury płaskiej, będącej poszukiwanym przekrojem. Mając dane rzuty prostych $n$ i $a$ możemy wyznaczyć ich ślady poziome $H_a$ i $H_n$. Łącząc ze sobą te ślady wyznaczymy ślad poziomy $h_{\alpha }$ płaszczyzny $\alpha$. Jak widać na rzucie poziomym ślad $h_{\alpha }$ (prosta leżąca na rzutni poziomej) przecina nam podstawę ostrosłupa w punktach $2^{\prime }$ i $3^{\prime }$ (podstawa ostrosłupa z założenia leży na rzutni poziomej). Łącząc rzuty poziome punktów $2^{\prime }$ i $3^{\prime }$ z rzutem poziomym $W^{\prime }$ wierzchołka, wyznaczymy rzut poziomy ($W^{\prime }{2}^{\prime }{3}^{\prime }$) trójkąta, który jest rzutem poszukiwanego przekroju. Prosta $n$ przecina boki przekroju w punktach $Q^{\prime }$ i $R^{\prime }$, które są punktami przebicia prostej $n$ ze ścianami ostrosłupa. Rzuty pionowe punktów przebicia znajdziemy na rzucie pionowym $n^{″}$ prostej oraz odnoszących punktów $Q^{\prime }$ i $R^{\prime }$. Ustalamy widoczność prostej $n$, przyjmując, że ściany ostrosłupa są nieprzezroczyste. Widoczność prostej $n$ w rzucie pionowym określamy analizując widoczność ścian ostrosłupa (ocenę przeprowadzamy w rzucie poziomym). Widać wyraźnie, że ściana $BCW$ jest widoczna w rzucie pionowym, natomiast ściana $ABW$ jest niewidoczna w rzucie pionowym. Prosta $n$ w rzucie pionowym będzie niewidoczna aż do punktu $R$ prostej ze ścianą $BCW$. Zaznaczamy to odpowiednio linią kreskową. Widoczność prostej $n$ w rzucie poziomym jest oczywista. Wszystkie ściany są widoczne z wyjątkiem podstawy. Prosta $n$, zatem jest niewidoczna wyłącznie między ścianami ostrosłupa, co odpowiednio zaznaczamy na rzucie poziomym przekroju.

---