CWGIĆwiczenie 2: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 49: | Linia 49: | ||
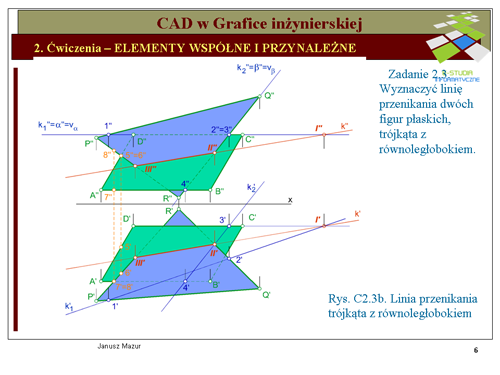
1). Wyznaczmy punkt przebicia boku '''''CD''''' równoległoboku z płaszczyzną trójkąta '''''PQR'''''. W tym celu poprowadzimy płaszczyznę pionowo - rzutującą <math>\alpha\,</math> przez bok '''''CD''''' równoległoboku. Płaszczyzna jest rzutująca, a więc krawędź przecięcia się tej płaszczyzny z płaszczyzną równoległoboku <math>k_1\,</math> będzie leżała w płaszczyźnie <math>\alpha\,</math>, ale również w płaszczyźnie trójkąta. Rzut pionowy tej krawędzi będzie pokrywał się z rzutem pionowym płaszczyzny <math>\alpha\,</math> oraz z rzutem pionowym boku <math>C''D''</math>. Przynależność krawędzi <math>k_1\,</math> do płaszczyzny trójkąta oznacza, że punkty <math>1''</math> i <math>2''</math> są rzutami punktów przecięcia się krawędzi z rzutami boków <math>P''Q''</math> oraz <math>R''Q''</math>. Rzuty poziome tych punktów znajdziemy na przecięciu się odnoszących prostopadłych do osi '''''x''''' z rzutami poziomymi boków trójkąta <math>P'Q'</math> oraz <math>R'Q'</math>. W ten sposób znajdujemy rzuty krawędzi <math>{k_1}''</math> oraz <math>{k_1}'</math>. W rzucie poziomym otrzymamy szukany punkt przebicia <math>{II}'</math> boku <math>C'D'</math> równoległoboku z płaszczyzną trójkąta. | 1). Wyznaczmy punkt przebicia boku '''''CD''''' równoległoboku z płaszczyzną trójkąta '''''PQR'''''. W tym celu poprowadzimy płaszczyznę pionowo - rzutującą <math>\alpha\,</math> przez bok '''''CD''''' równoległoboku. Płaszczyzna jest rzutująca, a więc krawędź przecięcia się tej płaszczyzny z płaszczyzną równoległoboku <math>k_1\,</math> będzie leżała w płaszczyźnie <math>\alpha\,</math>, ale również w płaszczyźnie trójkąta. Rzut pionowy tej krawędzi będzie pokrywał się z rzutem pionowym płaszczyzny <math>\alpha\,</math> oraz z rzutem pionowym boku <math>C''D''</math>. Przynależność krawędzi <math>k_1\,</math> do płaszczyzny trójkąta oznacza, że punkty <math>1''</math> i <math>2''</math> są rzutami punktów przecięcia się krawędzi z rzutami boków <math>P''Q''</math> oraz <math>R''Q''</math>. Rzuty poziome tych punktów znajdziemy na przecięciu się odnoszących prostopadłych do osi '''''x''''' z rzutami poziomymi boków trójkąta <math>P'Q'</math> oraz <math>R'Q'</math>. W ten sposób znajdujemy rzuty krawędzi <math>{k_1}''</math> oraz <math>{k_1}'</math>. W rzucie poziomym otrzymamy szukany punkt przebicia <math>{II}'</math> boku <math>C'D'</math> równoległoboku z płaszczyzną trójkąta. | ||
Rzut pionowy tego punktu wyznaczymy jako przecięcie odnoszącej z rzutem pionowym krawędzi <math>{k_1}''</math> (oraz boku <math>C''D''</math>). | |||
2). Podobną konstrukcję przeprowadzamy z inną parą np.: boku trójkąta oraz płaszczyzny równoległoboku '''''ABCD'''''. Wybierzmy do rozważań bok '''''RQ''''' trójkąta, przez który poprowadzimy płaszczyznę <math>\beta\,</math> a następnie, w drodze postępowania analogicznego jak poprzednio, wyznaczymy krawędź przecięcia się płaszczyzny <math>\beta\,</math> z płaszczyzną równoległoboku oraz w konsekwencji punkt przebicia '''''III''''' boku '''''QR''''' z równoległobokiem '''''ABCD'''''. | |||
Podobnie jak w poprzednim zadaniu ustalamy widoczność poszczególnych krawędzi analizując odpowiednio wysokość i głębokość punktów znajdujących się na przecięciu się rzutów poszczególnych boków figur płaskich. Dla rzutu pionowego analizujemy głębokości punktów 2 i 3, dla rzutu poziomego – wysokości punktów 7 i 8. Po analizie oznaczamy krawędzie i płaszczyzny widoczne oraz niewidoczne. | |||
|} | |} | ||
<hr width="100%"></math> | <hr width="100%"></math> | ||
Wersja z 16:23, 7 sie 2006
</math>