CWGIĆwiczenie 2: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 32: | Linia 32: | ||
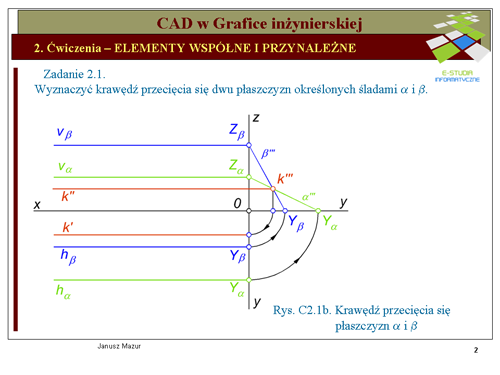
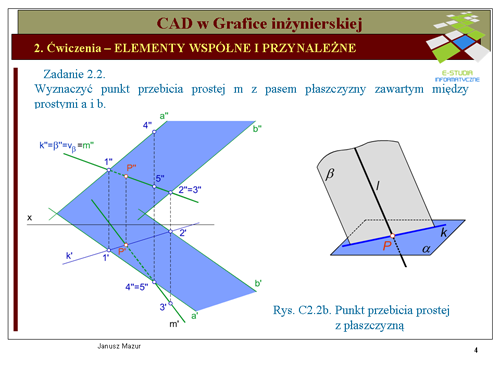
Jak widać z przedstawionego schematu postępowania punkty należące do krawędzi '''''k''''' będą należały jednocześnie do płaszczyzn <math>\alpha\,</math> i <math>\beta\,</math>. Zatem punkt przecięcia się prostej '''''m''''' z krawędzią '''''k''''' będzie punktem wspólnym prostej '''''m''''' i płaszczyzny <math>\alpha\,</math> (będzie punktem przebicia płaszczyzny <math>\alpha (a||b)\,</math> przez prostą '''''m''''' - rys. C2.2b). | Jak widać z przedstawionego schematu postępowania punkty należące do krawędzi '''''k''''' będą należały jednocześnie do płaszczyzn <math>\alpha\,</math> i <math>\beta\,</math>. Zatem punkt przecięcia się prostej '''''m''''' z krawędzią '''''k''''' będzie punktem wspólnym prostej '''''m''''' i płaszczyzny <math>\alpha\,</math> (będzie punktem przebicia płaszczyzny <math>\alpha (a||b)\,</math> przez prostą '''''m''''' - rys. C2.2b). | ||
Dla wygody dalszego postępowania poprowadźmy przez prostą '''''m''''' płaszczyznę pionowo-rzutujacą <math>\beta\,</math>. Ponieważ płaszczyzna <math>\beta\,</math> jest rzutująca, to wszystkie elementy płaskie znajdujące się w tej płaszczyźnie w rzucie pionowym będą leżały na rzucie pionowym płaszczyzny <math>\beta\,</math> (ślad pionowy płaszczyzny | Dla wygody dalszego postępowania poprowadźmy przez prostą '''''m''''' płaszczyznę pionowo-rzutujacą <math>\beta\,</math>. Ponieważ płaszczyzna <math>\beta\,</math> jest rzutująca, to wszystkie elementy płaskie znajdujące się w tej płaszczyźnie w rzucie pionowym będą leżały na rzucie pionowym płaszczyzny <math>\beta\,</math> (ślad pionowy płaszczyzny <math>v_{\beta}\,</math> będzie pokrywał się z rzutem płaszczyzny <math>\beta\,</math>). Zatem rzut pionowy krawędzi <math>k''</math>, przecięcia się płaszczyzn <math>\alpha\,</math> i <math>\beta\,</math> będzie również pokrywał się z rzutem pionowym płaszczyzny <math>\beta\,</math>. Krawędź '''''k''''' należy również do płaszczyzny <math>\alpha\,</math>, a więc rzut pionowy krawędzi <math>k''</math> przecina proste <math>a''</math> i <math>b''</math>, tworzące tą płaszczyznę, odpowiednio w punktach <math>1''</math> i <math>2''</math>. Rzuty poziome tych punktów wyznaczymy na rzutach poziomych prostych '''''a''''' i '''''b'''''. Następnie znajdujemy punkt przecięcia się wyznaczonej krawędzi z prostą '''''m'''''. W rzucie pionowym obie proste pokrywają się, więc wyznaczenie tego punktu jest niemożliwe, natomiast w rzucie poziomym bez trudu wyznaczymy rzut poziomy <math>P'</math> poszukiwanego punktu przebicia '''''P'''''. Na odnoszącej i rzutach pionowych prostych '''''k''''' i '''''m''''' będzie znajdował się rzut pionowy punktu przebicia <math>P''</math>. | ||
|} | |} | ||
<hr width="100%"> | <hr width="100%"> | ||