CWGI Moduł 4: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 125: | Linia 125: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:CWGI_M4_Slajd11.png]] | |valign="top" width="500px"|[[Grafika:CWGI_M4_Slajd11.png]] | ||
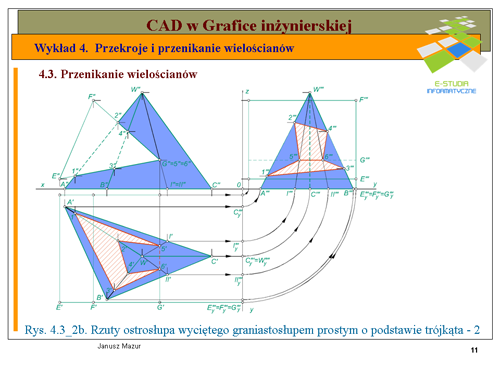
|valign="top"| | |valign="top"|W pierwszej kolejności uzupełniamy założenia o wyznaczenie trzecich rzutów ostrosłupa i graniastosłupa wycinającego (rys.4.3_2b). Rzutowanie ostrosłupa na trzecia, prostopadłą do rzutni <math>\Pi_1</math> i <math>\Pi_2</math> rozpoczynamy od przeniesienia rzutu podstawy na oś y między rzutnią <math>\Pi_1</math> a rzutnią <math>\Pi_3</math>. Po obrocie osi <math>y\,</math> do pokrycia się z osią <math>x\,</math> wyznaczymy (po rozwinięciu układu trzech rzutni) trzeci rzut podstawy <math>A"'</math>,<math>B"'</math>,<math>C"'</math>. Podobnie czynimy z wierzchołkiem <math>W\,</math>. Po obrocie i przeniesieniu rzutu poziomego do trzeciej rzutni, odmierzamy wysokość ostrosłupa, która oczywiście wyznaczy nam trzeci rzut wierzchołka <math>W"'</math>. | ||
Podobnie przenosimy do trzeciej rzutni graniastosłup <math>EFG</math>, którego krawędzie w trzecim rzucie będą równoległe do osi <math>y\,</math> po obrocie. | |||
Zarówno w rzutach pionowym i poziomym, jak również w rzucie trzecim ustalamy widoczność krawędzi analizując każdy rzut z kierunku prostopadłego do określonej rzutni. Widoczność krawędzi w rzutach pionowym i bocznym analizujemy poprzez obserwacje rzutu poziomego z kierunku prostopadłego do osi odpowiednio <math>x\,</math> i <math>y\,</math>. | |||
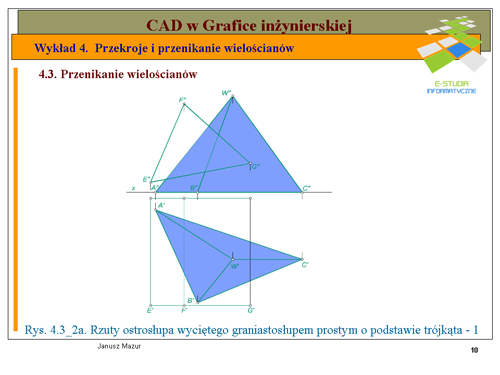
Wyznaczenie linii przenikania rozpoczynamy od rzutu pionowego obu wielościanów. Wyznaczamy w rzucie pionowym punkty przebicia krawędzi ostrosłupa z e ścianami graniastosłupa. Rzutujący charakter ścian graniastosłupa ułatwia nam wyznaczenie rzutów pionowych punktów przebicia krawędzi ostrosłupa ze ścianami graniastosłupa. Możemy, zatem określić rzuty pionowe punktów przebicia <math>1"</math>,<math>2"</math>,<math>3"</math>,<math>4"</math>. Punkt <math>G"</math> graniastosłupa będzie pokrywał się z dwoma rzutami punktów przebicia tej krawędzi graniastosłupa ze ścianami <math>AC</math> i <math>BC</math> ostrosłupa, a mianowicie <math>5"</math> i <math>6"</math>. Wyznaczono, zatem wszystkie punkty przebicia krawędzi jednego wielościanu ze ścianami drugiego wielościanu i odwrotnie. | |||
Kolejnym krokiem jest wyznaczenie pozostałych rzutów punktów przebicia, będących wierzchołkami odcinków linii przenikani wielościanów. Za pomocą linii odnoszących rzutowania ustalone zostają rzuty pionowe linii przenikania <math>1'</math>, <math>2'</math>, <math>3'</math>, <math>4'</math>, <math>5'</math>, <math>6'</math> oraz <math>1'"</math>, <math>2"'</math>, <math>3'"</math>, <math>4'"</math>,<math>5'"</math>,<math>6'"</math>. Ustalenie widoczności w przypadku usunięcia wykrojnika trójkątnego, nie powinno słuchaczom sprawić większego kłopotu, a wiec zagadnienie to pominiemy w rozwiązaniu tego zadania. | |||
|} | |} | ||
Wersja z 13:12, 7 sie 2006

|
Wykład 4. Przekroje i przenikanie wielościanów |

|