CWGI Moduł 4

Wykład 4. Przekroje i przenikanie wielościanów

---

Celem naszym będzie poszukiwanie rzutów punków przebicia prostej z wielościanem. Niech będą dane rzuty ostrosłupa prostego stojącego na rzutni poziomej $ABCW$ oraz rzuty prostej $n$. Należy wyznaczyć punkty przebicia prostej ze ścianami ostrosłupa oraz ustalić widoczność prostej przy założeniu, że ściany ostrosłupa są niewidoczne (patrz rys.4.1_1a). Ustalmy tok postępowania przy rozwiązaniu tego zadania: przez dowolny punkt $P$ leżący na prostej $n$ oraz wierzchołek $W$ ostrosłupa poprowadźmy prostą $a$, dwie proste $a$ i $n$ wyznaczą płaszczyznę $\alpha$. Wyznaczamy przekrój ostrosłupa płaszczyzną $\alpha$, w której leży dana prosta $n$ w punktach przecięcia się boków wielokąta przekroju z prostą $n$ wyznaczymy poszukiwane punkty przebicia ścian ostrosłupa z prostą $n$. Obierając punkt $P$ na prostej $n$ oraz prowadząc prostą a przez punkt $P$ i wierzchołek $W$ ostrosłupa wyznaczamy przekrój ostrosłupa płaszczyzną określoną przez te proste. Wierzchołek $W$ będzie stanowił jeden z wierzchołków figury płaskiej, będącej poszukiwanym przekrojem. Mając dane rzuty prostych $n$ i $a$ możemy wyznaczyć ich ślady poziome $H_a$ i $H_n$. Łącząc ze sobą te ślady wyznaczymy ślad poziomy $h_{\alpha }$ płaszczyzny $\alpha$. Jak widać na rzucie poziomym ślad $h_{\alpha }$ (prosta leżąca na rzutni poziomej) przecina nam podstawę ostrosłupa w punktach $1^{\prime }$ i $2^{\prime }$ (podstawa ostrosłupa z założenia leży na rzutni poziomej). Łącząc rzuty poziome punktów $1^{\prime }$ i $2^{\prime }$ z rzutem poziomym $W^{\prime }$ wierzchołka, wyznaczymy rzut poziomy ($W^{\prime }{1}^{\prime }{2}^{\prime }$) trójkąta, który jest rzutem poszukiwanego przekroju. Prosta $n$ przecina boki przekroju w punktach $Q^{\prime }$ i $R^{\prime }$, które są punktami przebicia prostej $n$ ze ścianami $\alpha$ ostrosłupa. Rzuty pionowe punktów przebicia znajdziemy na rzucie pionowym Parser nie mógł rozpoznać (błąd składni): {\displaystyle n"} prostej oraz odnoszących punktów $Q^{\prime }$ i $R^{\prime }$. Ustalamy widoczność prostej $n$, przyjmując, że ściany ostrosłupa są nieprzezroczyste. Widoczność prostej $n$ w rzucie pionowym określamy analizując widoczność ścian ostrosłupa (ocenę przeprowadzamy w rzucie poziomym). Widać wyraźnie, że ściana $ACW$ jest widoczna w rzucie pionowym, natomiast ściana $ABW$ jest niewidoczna w rzucie pionowym. Zaznaczamy to odpowiednio linią kreskową. Widoczność prostej $n$ w rzucie poziomym jest oczywista. Wszystkie ściany są widoczne z wyjątkiem podstawy. Prosta $n$, zatem jest niewidoczna wyłącznie między ścianami ostrosłupa, co odpowiednio zaznaczamy na rzucie poziomym przekroju.

---

Kolejnym zadaniem będzie poszukiwanie punktów przebicia prostej $n$ ze ścianami graniastosłupa pochyłego $ABC$ stojącego na rzutni poziomej. Pierwszym etapem rozwiązania zadania jest wyznaczenie rzutów przekroju graniastosłupa płaszczyzn, w której znajduje się dana prosta $n$. W tym celu przez prostą $n$ prowadzimy dowolna płaszczyznę. Dla ułatwienia będzie to płaszczyzna pionowo – rzutująca $\alpha$, prostopadła do rzutni pionowej. Ślad pionowy płaszczyzny $v_{\alpha }$ będzie pokrywał się z rzutem pionowym prostej $n$, ponieważ wszystkie elementy płaskie znajdujące się w takiej płaszczyźnie w rzucie pionowym rzutują się na ślad pionowy płaszczyzny, będący jednocześnie rzutem pionowym płaszczyzny. Kolejnym etapem rozwiązania jest wyznaczenie przekroju graniastosłupa płaszczyzną $\alpha$. Przekrój w rzucie pionowym wyznaczymy natychmiast. Zgodnie z cytowaną wyżej zasadą punkty przekroju Parser nie mógł rozpoznać (błąd składni): {\displaystyle 1", 2", 3"} w rzucie pionowym będą leżały na przecięciu się krawędzi graniastosłupa Parser nie mógł rozpoznać (błąd składni): {\displaystyle A",B", C"} ze śladem pionowym płaszczyzny $\alpha$. Rzuty poziome punktów przekroju $1^{\prime },2^{\prime },3^{\prime }$ będą leżały na przecięciu się odnoszących z rzutami poziomymi krawędzi graniastosłupa $A^{\prime },B^{\prime },C^{\prime }$. W miejscach gdzie prosta n przecina się z bokami przekroju otrzymamy poszukiwane punkty przebicia graniastosłupa prostą $n$. Dla pełnego rozwiązania zadania należy ustalić widoczność prostej, która wbija się w ściany graniastosłupa. W rzucie pionowym punkty przebicia znajdują się na ścianach widocznych, zatem prosta $n$ będzie niewidoczna jedynie na odcinku między punktami przebicia. W rzycie poziomym jeden z punktów przebicia (punkt $Q^{\prime }$) leży na ścianie niewidocznej Parser nie mógł rozpoznać (błąd składni): {\displaystyle B’ C’} , więc prosta $n$ będzie niewidoczna nie tylko między punktami przebicia ale również do miejsca wyjścia prostej z raniastosłupa. Niewidoczne krawędzie zaznaczono odpowiednio linią kreskową.

---

Kolejno naszym celem będzie wyznaczenie linii przenikania ostrosłupa $ABCW$ z płaszczyzną trójkąta $MNP$. Należy również ustalić widoczność poszczególnych krawędzi ostrosłupa oraz boków trójkąta (rys. 4.2_1a) Na poprzednim wykładzie zapoznaliśmy się z wyznaczaniem przekroju wielościanu płaszczyznami w położeniu rzutującym. W takim przypadku rozwiązanie zadania jest stosunkowo proste i nie wymaga żmudnych konstrukcji pomocniczych. W przypadku tego zadania mamy do czynienia z wyznaczaniem przekroju ostrosłupa (linia przenikania trójkąta z ostrosłupem jest częścią przekroju ostrosłupa płaszczyzną przechodzącą przez płaszczyznę trójkąta) z płaszczyzną bezśladową, w położeniu ogólnym. Rozwiązanie zadania uprościmy sprowadzając zaprezentowany w założeniach układ do układu, w którym płaszczyzna trójkąta jest w położeniu rzutującym. Zmianę układu odniesienia przeprowadzimy za pomocą omówionej na wcześniej transformacji. W tym celu obieramy w płaszczyźnie trójkąta $NMP$ prostą poziomą $a$. Oś $x_{1/3}$ nowego układu rzutni, która zmieni układ w taki sposób, aby płaszczyzna trójkąta była w położeniu rzutującym względem nowej rzutni, będzie prostopadła do rzutu poziomego prostej poziomej $a^{\prime }$. Kolejny etap - to dokonanie transformacji płaszczyzny trójkąta oraz ostrosłupa. Otrzymamy trzecie rzuty tych elementów przestrzennych, przy czym płaszczyzna $\alpha (MNP)$ znajduje się w położeniu rzutującym względem rzutni. Wyznaczenie przekroju ostrosłupa w trzecim rzucie jest zagadnieniem prostym. Wierzchołki przekroju będą leżały na przecięciu się trzeciego rzutu płaszczyzny trójkąta $MNP-{\alpha }^{‴}$ z krawędziami ostrosłupa. Za pomocą odnoszących prostopadłych do osi $x_{1/3}$ wyznaczymy rzuty poziome wierzchołków $I^{\prime }$, $I{I}^{\prime }$, $II{I}^{\prime }$, przekroju na rzutach poziomych boków trójkąta, a następnie za pomocą odnoszących prostopadłych do osi x wyznaczymy rzuty pionowe wierzchołków przekroju $I^{″}$, $I{I}^{″}$, $II{I}^{″}$, na rzutach pionowych boków ostrosłupa. Linia przenikania trójkąta z ostrosłupem będzie stanowiła tą część przekroju, która jest wspólna dla trójkąta i ścian ostrosłupa. Zakładając, że ściany ostrosłupa oraz płaszczyzna trójkąta są nieprzezroczyste ustalamy widoczność poszczególnych linii przenikania. Podobnie jak w poprzednich zadaniach widoczność w rzucie pionowym oceniamy analizując poszczególne linie przenikania na ścianach ostrosłupa w rzucie poziomym.

---

Zadanie o podobnej treści można rozwiązać przyjmując dowolną płaszczyznę przekroju w postaci płaszczyzny zadanej śladami (rys.4.2_1b). W tym przypadku należy zmienić układ odniesienia za pomocą transformacji, sprowadzając płaszczyznę $\alpha$ do położenia rzutującego. Przenosząc również ostrosłup do nowego układu za pomocą transformacji o takiej samej osi transformacji można wyznaczyć przekrój w trzecim rzucie podobnie jak w poprzednich zadaniach. Oś transformacji obieramy prostopadle do śladu poziomego płaszczyzny $\alpha$. Otrzymamy trzeci rzut węzła płaszczyzny Parser nie mógł rozpoznać (błąd składni): {\displaystyle X_\alpha"’} , który będzie jednym z punktów należących do trzeciego rzutu płaszczyzny $\alpha$. Należy, zatem wyznaczyć jeszcze trzeci rzut dowolnego punktu należącego do płaszczyzny $\alpha$, aby wyznaczyć trzeci rzut płaszczyzny. W tym celu obieramy dowolnie położony punkt Parser nie mógł rozpoznać (błąd składni): {\displaystyle 1"} , należący do śladu pionowego płaszczyzny $\alpha$. Drugi rzut poziomy $1^{\prime }$ będzie leżał na osi $x$. Dokonując transformacji punktu $1$ (odmierzamy od osi transformacji wielkość równą wysokości punktu $1$) wyznaczymy rzut Parser nie mógł rozpoznać (błąd składni): {\displaystyle 1"'} . Punkty Parser nie mógł rozpoznać (błąd składni): {\displaystyle 1"'} i Parser nie mógł rozpoznać (błąd składni): {\displaystyle X_\alpha"'} wyznaczą nam Parser nie mógł rozpoznać (błąd składni): {\displaystyle \alpha"'} . Przenosimy następnie ostrosłup do nowego układu, dokonując transformacji poszczególnych wierzchołków ostrosłupa $ABCDW$. Po dokonaniu transformacji płaszczyzny $\alpha$ i ostrosłupa można wyznaczyć trzecie rzuty wierzchołków przekroju ostrosłupa w miejscu przecięcia się Parser nie mógł rozpoznać (błąd składni): {\displaystyle \alpha"'} z krawędziami Parser nie mógł rozpoznać (błąd składni): {\displaystyle A"'W"'} , Parser nie mógł rozpoznać (błąd składni): {\displaystyle B"'W"'} , Parser nie mógł rozpoznać (błąd składni): {\displaystyle C"'W"'} , Parser nie mógł rozpoznać (błąd składni): {\displaystyle D"'W"'} oraz z bokami podstawy (jak widać w trzecim rzucie płaszczyzna przecina również podstawę). Otrzymamy w trzecim rzuci pięć wierzchołków figury będącej przekrojem ostrosłupa (Parser nie mógł rozpoznać (błąd składni): {\displaystyle 2"'} ,Parser nie mógł rozpoznać (błąd składni): {\displaystyle 3"'} ,Parser nie mógł rozpoznać (błąd składni): {\displaystyle 4"'} ,Parser nie mógł rozpoznać (błąd składni): {\displaystyle 5"'} ,Parser nie mógł rozpoznać (błąd składni): {\displaystyle 6"'} ). Powracając do układu dwu rzutni, poziomej i pionowej otrzymamy rzuty przekroju. Zamiast ustalenia widoczności poszczególnych krawędzi, można wyznaczyć rzuty bryły powstałej po „wygaszając” odciętą płaszczyzna przekroju część ostrosłupa.

---

W technice często mamy do czynienia z zagadnieniem przenikania się powierzchni regularnych wielościanów. Ustalenie linii przenikania - konstrukcyjnie pozwala konstruktorowi przewidzieć szereg kwestii technicznych wynikających z tego tytułu. Wykorzystując metody przedstawione w dotychczasowych rozdziałach omówimy przykładowe przenikanie się dwóch wielościanów. Należy wyznaczyć linię przenikania ostrosłupa $KLNW$ z graniastosłupem prostym stojącym na rzutni poziomej oraz podstawie $ABCD$. Na rysunku 4.3_1a przedstawione zostały założenia do niniejszego zadania. Graniastosłup prosty, którego podstawa $ABCD$ leży na rzutni poziomej ma ściany w położeniu rzutującym względem tej rzutni. Wszystkie elementy płaskie leżące na ścianach graniastosłupa, w rzucie poziomym, będą znajdowały się na rzucie poziomym boków podstawy $A^{\prime }{B}^{\prime }$, $B^{\prime }{C}^{\prime }$, $C^{\prime }{D}^{\prime }$, $D^{\prime }{A}^{\prime }$. Dla ułatwienia i czytelności rysunku nie oznaczymy górnej podstawy graniastosłupa, która jak widać z rzutu pionowego nie bierze udziału w tworzeniu linii przenikania. Położenie ostrosłupa wymaga ustalenia widoczności jego krawędzi. Widoczność tą powinniśmy ustalić w rzucie pionowym, ponieważ w rzucie poziomym odpowiednie krawędzie podstaw pokrywają się i rzuty górnych SA widoczne. W tym celu wykorzystamy punkty $EF$ leżące odpowiednio: $E$ na boku podstawy $LN$ oraz $F$ na krawędzi $KW$ ostrosłupa. Rzuty pionowe tych punktów pokrywają się. Zważywszy, że punkt $F$ należący do krawędzi $KW$ ma większą głębokość (większą odległość od rzutni pionowej) można stwierdzić, iż w rzucie pionowym bok podstawy ostrosłupa $L^{″}{N}^{″}$ będzie niewidoczny, co zaznaczamy linią kreskową.

---

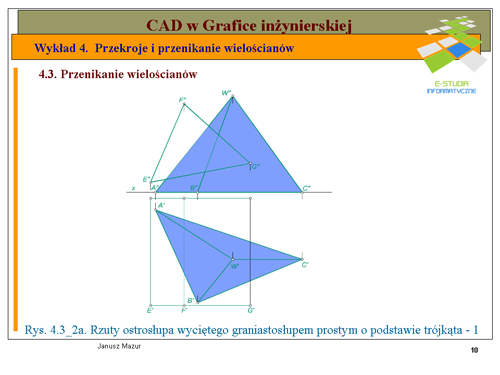
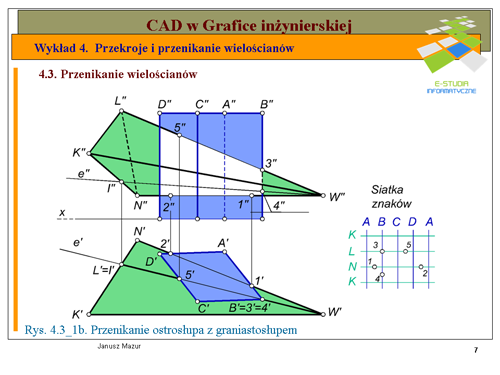
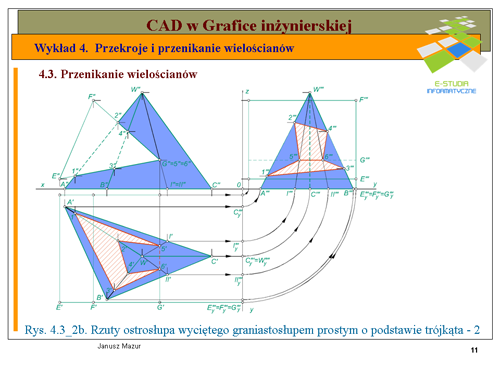
Linia przenikania wielościanów związana jest z wyznaczaniem punktów przebicia ścian jednego z wielościanów krawędziami drugiego wielościanu. Dokonajmy, zatem analizy podanych wielościanów w aspekcie ich położenia względem siebie. Na rys. 4.3_1b, w rzucie poziomym możemy zaobserwować, które krawędzie jednego z wielościanów przebijają ściany drugiego wielościanu. Krawędź $A$ graniastosłupa leży poza ostrosłupem i nie bierze udziału w tworzeniu poszukiwanej linii przenikania. Pozostałe krawędzie graniastosłupa przebijają ściany ostrosłupa. Krawędź $B$ przecina krawędź $LW$ oraz ścianę $KNW$ ostrosłupa, krawędź $C$ graniastosłupa przebija ściany $KNW$ i $KLW$ ostrosłupa. Krawędź $D$ graniastosłupa przebija ściany $LNW$ oraz $KNW$. Podobnie można ocenić, które krawędzie ostrosłupa przebijają ściany graniastosłupa. Krawędź $NW$ ostrosłupa przebija ściany $DA$ i $AB$ graniastosłupa, natomiast krawędź $LW$ przebija ścianę $CD$ oraz przecina (opisaną wcześniej) krawędź $B$ graniastosłupa. Krawędź $KW$ nie bierze udziału w tworzeniu linii przenikania. Po takiej analizie możemy przystąpić do wyznaczania poszczególnych punktów linii przenikania. Oznaczmy poszczególne punkty przebicia i przecięcia krawędzi ostrosłupa ze ścianami i krawędzią graniastosłupa, opisane powyżej, w rzucie poziomym kolejno punktami $1^{\prime },2^{\prime },3^{\prime },4^{\prime },5^{\prime }$. Rzuty pionowe punktów $1^{″},2^{″},3^{″},5^{″}$ znajdziemy bezpośrednio na rzucie pionowym krawędzi ostrosłupa. Jedyny problem rozwiązania stanowi rzut pionowy punktu $4^{″}$, który znajduje się na ścianie $KNW$ ostrosłupa. W celu wyznaczenia jego położenia poprowadźmy przez rzut poziomy wierzchołka $W^{\prime }$ ostrosłupa i rzut poziomy punktu $4^{\prime }$ tworzącą $e^{\prime }$, leżącą na ścianie $K^{\prime }{N}^{\prime }{W}^{\prime }$. Następnie wyznaczymy rzut pionowy tworzącej $e^{″}$, korzystając pośrednio z rzutów punktów $I^{\prime }$ i $I{I}^{″}$ przecięcia tworzącej z bokiem $KN$ podstawy ostrosłupa, na rzucie pionowym $e^{″}$ wyznaczymy poszukiwany rzut pionowy punktu $4^{″}$. W etapie $I$ ustalone zostały punkty przebicia krawędzi ostrosłupa ze ścianami graniastosłupa. 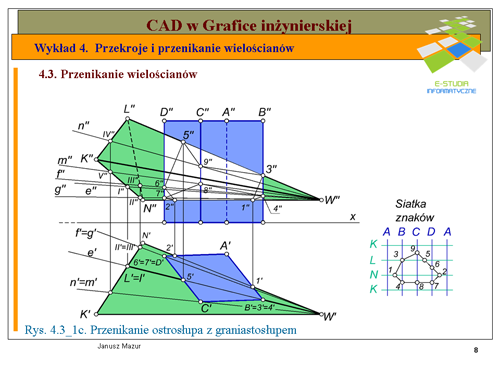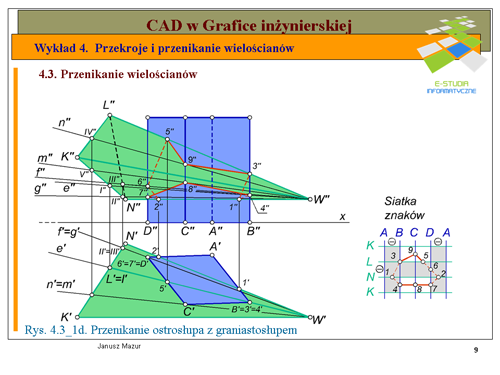W celu określenia kolejności połączenia punktów tworzących linie przenikania zbudujemy tzw. siatkę znaków. Rozetnijmy poszczególne wielościany wzdłuż jednej z krawędzi (najlepiej według krawędzi niebiorącej udziału w tworzeniu linii przenikania) i oznaczmy te krawędzie symbolicznie na przedstawionej siatce, powtarzając pierwszą krawędź tak, aby zamknąć powierzchnię boczną danego wielościanu. Na tak stworzonej siatce nanosimy symbolicznie poszczególne punkty linii przenikania. Np. punkt $1$ znajduje się na krawędzi $N$ ostrosłupa oraz ścianie $AB$ graniastosłupa. Podobnie postępujemy z następnymi punktami.

---

---

---

---

---