CWGI Moduł 3: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 27: | Linia 27: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:CWGI_M3_Slajd4.png]] | |valign="top" width="500px"|[[Grafika:CWGI_M3_Slajd4.png]] | ||
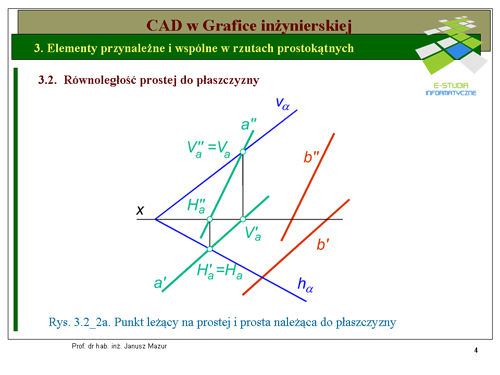
|valign="top"|Bardziej złożona jest konstrukcja równoległości prostej do płaszczyzny w przypadku, gdy płaszczyzna określona jest śladami (rys. 3.2_2a). Wynika to z konieczności wyznaczenia w pierwszej kolejności prostej <math>a\,</math> leżącej w płaszczyźnie. Przypomnijmy tu warunek przynależności prostej do płaszczyzny (ślady prostej muszą leżeć na śladach płaszczyzny). Po wyznaczeniu rzutów prostej '''a''' leżącej w płaszczyźnie <math>\alpha\,</math>bez trudu można wyznaczyć rzuty prostej <math>b || \alpha</math> Rzut pionowy prostej <math>b''</math> będzie równoległy do rzutu pionowego prostej <math>a''</math>, natomiast rzut poziomy prostej <math>b'</math> będzie równoległy do rzutu poziomego prostej <math>a''</math> jeżącej w płaszczyźnie <math>\alpha\,</math>. | |valign="top"|Bardziej złożona jest konstrukcja równoległości prostej do płaszczyzny w przypadku, gdy płaszczyzna określona jest śladami (rys. 3.2_2a). Wynika to z konieczności wyznaczenia w pierwszej kolejności prostej <math>a\,</math> leżącej w płaszczyźnie. Przypomnijmy tu warunek przynależności prostej do płaszczyzny (ślady prostej muszą leżeć na śladach płaszczyzny). Po wyznaczeniu rzutów prostej '''a''' leżącej w płaszczyźnie <math>\alpha\,</math>bez trudu można wyznaczyć rzuty prostej <math>b || \alpha</math> Rzut pionowy prostej <math>b''</math> będzie równoległy do rzutu pionowego prostej <math>a''</math>, natomiast rzut poziomy prostej <math>b'\,</math> będzie równoległy do rzutu poziomego prostej <math>a''</math> jeżącej w płaszczyźnie <math>\alpha\,</math>. | ||
|} | |} | ||
| Linia 36: | Linia 36: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:CWGI_M3_Slajd5.png]] | |valign="top" width="500px"|[[Grafika:CWGI_M3_Slajd5.png]] | ||
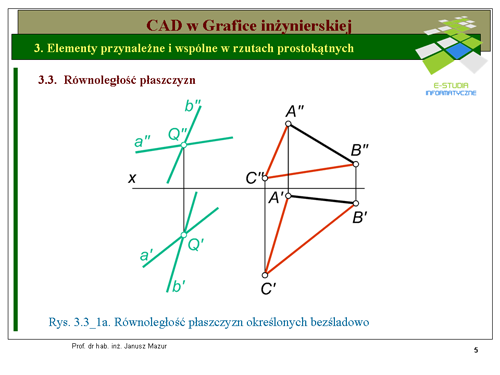
|valign="top"|Równoległość płaszczyzn w rzutach prostokątnych można zdefiniować w sposób następujący:, jeżeli dwie przecinające się proste są równoległe do dwóch innych, przecinających się prostych, to płaszczyzny, jakie tworzą te proste są do siebie równoległe. Można to przedstawić na rys. 3.3_1a. Jedna z płaszczyzn jest określona przez dwie proste przecinające się, druga również, lecz w postaci trójkąta. Płaszczyzna określona przy pomocy dwóch prostych <math>(a x b)</math> przecinających się w punkcie <math>Q\,</math> jest równoległa do płaszczyzny <math>\Delta (ABC)</math>, ponieważ rzuty prostych <math>a\ i\ b</math> są odpowiednio równoległe do rzutów boków <math>AC\ i CB\\Delta (ABC)</math>. | |valign="top"|Równoległość płaszczyzn w rzutach prostokątnych można zdefiniować w sposób następujący:, jeżeli dwie przecinające się proste są równoległe do dwóch innych, przecinających się prostych, to płaszczyzny, jakie tworzą te proste są do siebie równoległe. Można to przedstawić na rys. 3.3_1a. Jedna z płaszczyzn jest określona przez dwie proste przecinające się, druga również, lecz w postaci trójkąta. Płaszczyzna określona przy pomocy dwóch prostych <math>(a x b)</math> przecinających się w punkcie <math>Q\,</math> jest równoległa do płaszczyzny <math>\Delta (ABC)</math>, ponieważ rzuty prostych <math>a\ i\ b</math> są | ||
odpowiednio równoległe do rzutów boków <math>AC\ i CB\ \Delta (ABC)</math>. | |||
|} | |} | ||
| Linia 88: | Linia 90: | ||
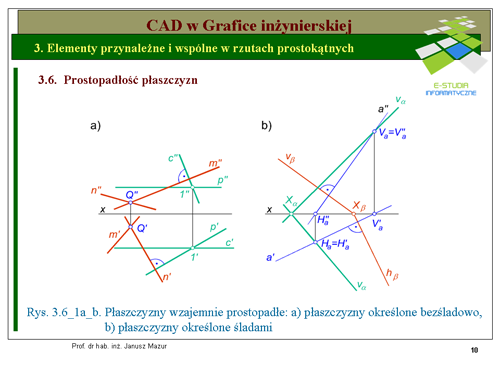
Na rys. 3.6_1a dana jest płaszczyzna określona za pomocą dwóch przecinających się w punkcie 1 prostych <math>p\ i\ c</math>. Druga płaszczyzna prostopadła do pierwszej określona została za pomocą również dwóch prostych m i n przecinających się w punkcie <math>Q\,</math>, przy czym jedna z nich jest prostopadła do płaszczyzny utworzonej przez proste <math>p\ i\ c</math>. Wynika to z faktu, iż proste <math>p\ i\ c</math> są odpowiednio równoległe do rzutni poziomej (prosta pozioma p) i rzutni pionowej (prosta czołowa c), a więc prosta <math>n\,</math> będzie prostopadła do płaszczyzny utworzonej przez te proste, jeżeli rzut pionowy prostej <math>n''</math> będzie prostopadły do rzutu pionowego prostej czołowej <math>c''</math>, a rzut poziomy prostej <math>n'</math> będzie prostopadły do rzutu poziomego prostej poziomej <math>p'</math>. | Na rys. 3.6_1a dana jest płaszczyzna określona za pomocą dwóch przecinających się w punkcie 1 prostych <math>p\ i\ c</math>. Druga płaszczyzna prostopadła do pierwszej określona została za pomocą również dwóch prostych m i n przecinających się w punkcie <math>Q\,</math>, przy czym jedna z nich jest prostopadła do płaszczyzny utworzonej przez proste <math>p\ i\ c</math>. Wynika to z faktu, iż proste <math>p\ i\ c</math> są odpowiednio równoległe do rzutni poziomej (prosta pozioma p) i rzutni pionowej (prosta czołowa c), a więc prosta <math>n\,</math> będzie prostopadła do płaszczyzny utworzonej przez te proste, jeżeli rzut pionowy prostej <math>n''</math> będzie prostopadły do rzutu pionowego prostej czołowej <math>c''</math>, a rzut poziomy prostej <math>n'</math> będzie prostopadły do rzutu poziomego prostej poziomej <math>p'</math>. | ||
W przypadku konstrukcji śladowych (rys. 3.6_1b) w dowolnej płaszczyźnie <math>\alpha</math>określonej śladami <math>v_\alpha i | W przypadku konstrukcji śladowych (rys. 3.6_1b) w dowolnej płaszczyźnie <math>\alpha</math>określonej śladami <math>v_\alpha i h_\alpha</math>obieramy dowolną prostą a leżącą w płaszczyźnie, a więc jej ślady <math>V_\alpha i H_\alpha</math> będą leżały na śladach płaszczyzny. W ten sposób skonstruowane rzuty prostej <math>a\,</math> leżącej w płaszczyźnie <math>\alpha\,</math> powinny być prostopadłe do odpowiednich śladów płaszczyzny <math>\beta</math>. Zatem możemy stwierdzić, że płaszczyzna <math>\beta</math> jest prostopadła do <math>\alpha</math>, ponieważ jest prostopadła do prostej <math>a\,</math>, która leży w płaszczyźnie <math>\alpha\,</math>. | ||
| Linia 97: | Linia 99: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:CWGI_M3_Slajd11.png]] | |valign="top" width="500px"|[[Grafika:CWGI_M3_Slajd11.png]] | ||
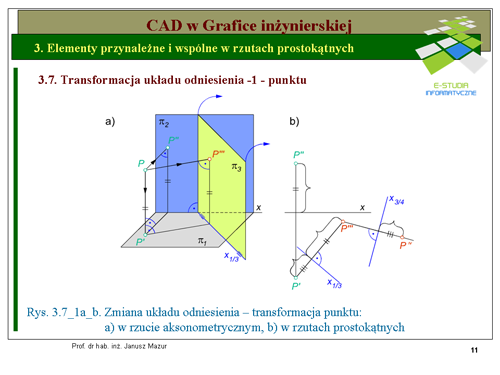
|valign="top"|Zmiana układu odniesienia w geometrii odwzorowań przestrzennych nazwana została transformacją. W celu dokonania transformacji punktu obieramy płaszczyznę <math> | |valign="top"|Zmiana układu odniesienia w geometrii odwzorowań przestrzennych nazwana została transformacją. W celu dokonania transformacji punktu obieramy płaszczyznę <math>\pi_3</math>, która jest prostopadła np. do rzutni poziomej, a następnie dokonujemy rzutowania prostokątnego na tą właśnie rzutnię. Na rys. 2.8a przykład ten zilustrowano w rzucie aksonometrycznym. Jak widać poza dwoma rzutami: pionowym i poziomym otrzymaliśmy trzeci rzut punktu oznaczany przez <math>P'''</math>. Trzecią rzutnię obracamy następnie dookoła osi transformacji, czyli krawędzi przecięcia się trzeciej rzutni z rzutnią poziomą, do położenia pokrywającego się z rzutnią poziomą. Przenosząc to rozważanie do układu rzutów prostokątnych, w celu wyznaczenia trzeciego rzutu punktu po dokonaniu transformacji układu odniesienia należy postępować w sposób następujący: | ||
1. obrać w sposób dowolny oś transformacji (ślad, krawędź przecięcia się nowej rzutni <math>pi_3</math> z rzutnią poziomą). Oś transformacji oznaczać będziemy <math>x_{1/3}</math> , | 1. obrać w sposób dowolny oś transformacji (ślad, krawędź przecięcia się nowej rzutni <math>\pi_3</math> z rzutnią poziomą). Oś transformacji oznaczać będziemy <math>x_{1/3}</math> , | ||
2. trzeci rzut punktu będzie leżał na odnoszącej prostopadłej do osi transformacji, co wynika z obrotu trzeciej rzutni <math>pi_3</math> do położenia na rzutni poziomej <math>pi_1</math> . Odległość, w jakiej będzie się znajdował trzeci rzut punktu <math>P'''</math> od osi <math>x\,</math> jest równa wysokości punktu <math>P\,</math>, czyli odległości tego punktu od rzutni poziomej. Ta odległość jest oczywiście taka sama jak odległość rzutu pionowego punktu <math>P''</math> od osi <math>x\ | 2. trzeci rzut punktu będzie leżał na odnoszącej prostopadłej do osi transformacji, co wynika z obrotu trzeciej rzutni <math>pi_3</math> do położenia na rzutni poziomej <math>pi_1</math> . Odległość, w jakiej będzie się znajdował trzeci rzut punktu <math>P'''</math> od osi <math>x\,</math> jest równa wysokości punktu <math>P\,</math>, czyli odległości tego punktu od rzutni poziomej. Ta odległość jest oczywiście taka sama jak odległość rzutu pionowego punktu <math>P''</math> od osi <math>x\,</math>. Można, zatem stwierdzić, iż odmierzamy od osi <math>x_{1/3}</math> odległość poprzedniego rzutu (<math>P"</math>) punktu od poprzedniej osi (x), | ||
3. taką operację możemy powtarzać w miarę potrzeby wielokrotnie, zachowując opisane powyżej zasady. Na rys. 3.7_1a,b przedstawiono dwie kolejne transformacje punktu <math>P\,</math> w rzucie aksonometrycznym i prostokątnym. | 3. taką operację możemy powtarzać w miarę potrzeby wielokrotnie, zachowując opisane powyżej zasady. Na rys. 3.7_1a,b przedstawiono dwie kolejne transformacje punktu <math>P\,</math> w rzucie aksonometrycznym i prostokątnym. | ||
Wersja z 12:25, 7 sie 2006

|
Elementy równoległe i prostopadłe |