CWGI Moduł 1

Rzutowanie w Grafice inżynierskiej Wykłady z przedmiotu "CAD w Grafice inżynierskiej " zawierają podstawowe wiadomości z odwzorowań elementów przestrzennych na płaszczyźnie rysunku, teorii zapisu konstrukcji technicznych oraz metod komputerowego wspomagania projektowania konstrukcji mechanicznych i elektromechanicznych. Grafika inżynierska, dla inżyniera ma niezwykle istotne znaczenie. Umożliwia dialog między twórcą konstrukcji technicznych a jej wykonawcą. Pozwala przekazać niezbędne informacje techniczne o produkcie konsumentowi. Realizowany w grafice inżynierskiej zapis konstrukcji można nazwać językiem inżynierów konstruktorów i technologów. W dobie rozwoju technik komputerowych i multimedialnych stosowanie użytkowych programów graficznych stanowi ważne uzupełnienie narzędzi projektanta.

---

Grafika inżynierska opiera się na prawach i ustaleniach nauki zwanej geometrią. Historycznie, geometria była zbiorem przepisów praktycznych, które dotyczyły wykonywania pomiarów fizycznych przedmiotów materialnych. W starożytności ok. 300 lat przed naszą erą ustalono dla niej znaczące miejsce w opracowaniach greckiego matematyka – Euklidesa. W dziele o nazwie Elementy autor nadał geometrii postać nauki abstrakcyjnej, gdzie przedmiot materialny zastąpiono pojęciem figury geometrycznej, będącej jego emanacją. Własności takiej figury dotyczyły głównie wielkości i kształtu przedmiotu, a więc opierały się na ustaleniu wzajemnych odległości należących do danego przedmiotu. Wprowadzono naukę o tzw. własnościach metrycznych, która charakteryzuje daną figurę oraz wszystkie figury do niej przystające. Przez figury definiowano zbiory punktów należących do pewnego stałego zbioru punktów zwanego przestrzenią, którą przypadku określenia odległości między punktami zbioru nazwano przestrzenią metryczną. Do najbardziej znanych przestrzeni metrycznych należą prosta euklidesowa $E_1$, płaszczyzna euklidesowa $E_2$ oraz przestrzeń trójwymiarowa $E_3$. Geometria euklidesowa zbudowana w oparciu o cztery podstawowe grupy aksjomatów (o przynależności, o uporządkowaniu, o porównaniu i ciągłości), uzupełnione o aksjomat zwany pewnikiem Euklidesa. W naszych rozważaniach będziemy zajmować się szczególnym przypadkiem geometrii zwanej geometrią wykreślną. Geometria wykreślna, której przedmiotem są metody odwzorowań obiektów przestrzennych na płaszczyźnie, jest teoretyczna podstawą sporządzania graficznych zapisów konstrukcji stosowanych w technice. Nauka o rzutowaniu jest przedmiotem niniejszego wykładu

---

Teoria aksjomatów, o którą oparta jest grafika inżynierska jest teorią abstrakcyjną, ściśle związaną z regułami znanymi w logice. Model tej teorii zbudowany z obiektów materialnych (np. punktów prostych i płaszczyzn) i oparty jest o jej założenia (aksjomaty). Geometria euklidesowa posiada jeden swój model, w którym pojęcia pierwotne, jak punkty, proste i płaszczyzny oraz występujące między nimi relacje, rozumiane są zgodnie z powszechną intuicją i nabytym doświadczeniem człowieka analizującego proces odwzorowań przestrzennych. W dalszych wykładach będziemy wykorzystywali rozważania w dwu lub trójwymiarowej przestrzeni kartezjańskiej. Będziemy również wykorzystywali zdefiniowane w literaturze przedmiotowej elementy niewłaściwe rozumiejąc między innymi, że: wszystkie proste równoległe przecinają się w punkcie niewłaściwym, wszystkie płaszczyzny równoległe przecinają się wzdłuż krawędzi, będącej prostą niewłaściwą, płaszczyzna niewłaściwa jest zbiorem punktów niewłaściwych i prostych niewłaściwych, wszystkich punktów i płaszczyzn przestrzeni.

---

Operacja odwzorowań przestrzennych opiera się o proces rzutowania. Stosowane są dwa podstawowe rodzaje rzutów stosowanych w technice. Jest to rzutowanie środkowe i rzutowanie równoległe. Przyjmijmy w trójwymiarowej przestrzeni euklidesowej punkt właściwy $S$, zwany środkiem rzutu oraz płaszczyznę $\pi$, zwana rzutnią. Zespół $R(\pi ,S)$ nazywamy aparatem projekcyjnym (elementami) rzutowania środkowego. Komputerowy zapis konstrukcji realizowany jest przy pomocy programu graficznego z grupy CAD amerykańskiej firmy Autodesk. Trzecia część wykładu realizowana jest w oparciu o graficzny program komputerowy AutoCAD Pl. Do każdego wykładu przygotowano ćwiczenia w postaci zadań konstrukcyjnych, pozwalających na ugruntowanie prezentowanego materiału.

---

Rzut środkowy punktu $P$ otrzymano prowadząc promień rzutujący $p$, wychodzący ze środka rzutowania $S$ i przechodzący przez ten punkt, aż do przecięcia się z rzutnią $\pi$Punkt przebicia promienia rzutującego z rzutnią $(P^{\prime })$ wyznacza rzut środkowy tego punktu.

---

Podobnie można wyznaczyć rzuty środkowe innych punktów w przestrzeni, np. punktów $QiR$, prowadząc odpowiednie promienie rzutujące $qir$ do przecięcia się z płaszczyzną rzutni $\pi$. Jak widać na rysunku odwzorowanie tego typu nie jest jednoznaczne. Punktowi w przestrzeni odpowiada jeden i tylko jeden rzut punktu na rzutni $\pi$, lecz rzutowi punktu odpowiada nieskończenie wiele punktów leżących w przestrzeni na promieniu rzutującym. Oznacza to potrzebę wprowadzenia dalszych parametrów, które zapewniałyby tą jednoznaczność, co jest warunkiem koniecznym poprawnej identyfikacji obiektów przestrzennych.

---

---

W przypadku rzutu równoległego postępujemy podobnie. Jednak promienie rzutujące są równoległe do zadanego kierunku rzutowania k. Rozważając w geometrii zasady rzutowania równoległego często mamy do czynienia z elementami niewłaściwymi, które zdefiniujemy dla zrozumienia zapisów umownych stosowanych w rzutowaniu. W geometrii euklidesowej dwie proste leżące na płaszczyźnie przecinają się lub są równoległe. Prosta nie leżąca w płaszczyźnie przebija ją lub jest do niej równoległa. Rozważania byłyby prostsze, gdyby dwie proste leżące w płaszczyźnie zawsze przecinały się, zaś prosta zawsze przebijała płaszczyznę. Wprowadzając określenie punktu niewłaściwego możemy uzyskać takie własności podstawowych elementów przestrzennych Do zbioru punktów właściwych, leżących na prostej dołączymy, zatem jeden punkt niewłaściwy w taki sposób, aby: proste równoległe miały wspólny punkt niewłaściwy, proste nierównoległe miały różne punkty niewłaściwe. Można, zatem powiedzieć, iż proste równoległe "przecinają się" w jednym punkcie niewłaściwym. Podobne rozumowanie możemy przeprowadzić w stosunku do dwóch płaszczyzn równoległych, które mieć będą wówczas "wspólną" krawędź przecięcia, zwaną prostą niewłaściwą. Punkty niewłaściwe oznaczać będziemy symbolem punktu właściwego ze znakiem "nieskończoność": np. A:, B:, ... Prostą niewłaściwą opisujemy przy pomocy odcinka prostej zakończonego strzałką, określającego kierunek prostej łącznie z symbolem punktu niewłaściwego tzn.: $k^{{\mathrm{\infty }}^{⟶}}$

---

Zauważmy, że własności rzutu $G^{\prime }$ tworu $G$ nie są identyczne jak własności samego tworu G. Wynika to między innymi z faktu, że twór może być bryłą przestrzenną, natomiast jego rzut równoległy zawsze jest figurą płaską. Jednak niektóre własności tworów nie ulegają zmianie po dokonaniu operacji rzutowania równoległego. Własności te nazwane zostały niezmiennikami rzutu równoległego. Niezmienniki rzutowania równoległego można opisać w sposób następujący: N1. współliniowość punktów (rzuty punktów leżących na prostej będą leżały na rzucie tej prostej), N2. przynależności elementów (jeżeli punkt leży na prostej, to rzut tego punktu leży na rzucie tej prostej), N3. równoległość prostych (rzutami prostych równoległych są proste równoległe lub punkty), N4. stosunek długości odcinków równoległych do siebie, nierównoległych do kierunku rzutowania, (jeżeli długości odcinków równoległych pozostają w określonym stosunku do siebie to długości ich rzutów pozostają w stosunku identycznym), N5. stosunek podziału odcinka (jeżeli punkt A dzieli odcinek w określonym stosunku, to rzut punktu A' dzieli rzut tego odcinka w takim samym stosunku), N6. długość odcinków równoległych do rzutni (długość odcinka równoległego do rzutni jest taka sama jak długość rzutu tego odcinka), N7. kąt o obu ramionach równoległych do rzutni (wielkość kąta, którego obydwa ramiona są równoległe do rzutni jest taka sama jak wielkość rzutu tego kąta), N8. związki miarowe w płaszczyźnie równoległej do rzutni (długości odcinków, kąty oraz wielkości figur leżących na płaszczyźnie równoległej do rzutni zachowują się po dokonaniu operacji rzutowania). Niezmienniki rzutowania równoległego stanowią własności o charakterze podstawowym, które będą wykorzystywane do zapisu konstrukcji technicznych na płaszczyźnie.

---

Znany z geometrii elementarnej układ osi współrzędnych, zwany układem kartezjańskim, jest układem przestrzennym i składa się z osi $x,y,z$ oraz początku układu współrzędnych 0. Osie przecinają się w punkcie początkowym każdej z nich pod kątami $90^o$ względem siebie. Umieszczony w takim układzie punkt $P$ będzie miał współrzędne $P(x_o,y_o,z_o)$. Analogicznie można zdefiniować położenie wektora i innych elementów w przestrzeni. Rzuty aksonometryczne są formą rzutów równoległych, które pozwalają przetransponować układ przestrzenny $0xyz$ na układ płaski, a więc układ umożliwiający odwzorowanie tworów przestrzennych na płaszczyźnie. Takim zagadnieniem jesteśmy zainteresowani z punktu widzenia graficznego zapisu konstrukcji. Rozwijając teorię rzutowania równoległego przyjmiemy twierdzenie Pohlke'go, które otworzy możliwości wyodrębnionego zapisu tworów przestrzennych zwanego rzutem aksonometrycznym. Twierdzenie to umożliwia przenoszenie brył przestrzennych do zupełnie dowolnych układów płaskich zwanych układami aksonometrycznymi. Stanowi to dla inżyniera źródło możliwości różnorodnego eksponowania swoich twórczych projektów.

---

Przyjmując do wiadomości ustalenia twierdzenia Pohlke'go można układ współrzędnych kartezjańskich, za pomocą rzutu równoległego, przetransponować na dowolny układ płaski. Ilustruje to rys.1.4a- 1.4c. Początek $0$ układu $0xyz$ oraz punkty jednostkowe $1x,1y,1z$, tworzą, bowiem czworościan 01x1y1z, który w myśl twierdzenia Pohlke’go można odwzorować na czworokąt zupełny Parser nie mógł rozpoznać (błąd składni): {\displaystyle 0’1x’1y’1z’} , podobny do z góry zadanego czworokąta zupełnego (czyli czworokąt dowolny). Ma to fundamentalne znaczenie dla konstruktorów. Oznacza, iż odwzorowanie przestrzennych brył na płaszczyznę można dokonywać w dowolnych układach równoległego rzutu aksonometrycznego, pod warunkiem opisania podstawowych jego parametrów, do których należą rozmieszczenie rzutów osi układu kartezjańskiego oraz tzw. skrótów aksonometrycznych wynikających z rzutowania równoległego układu.

---

Dla potrzeb graficznego zapisu konstrukcji, w wyniku doświadczeń praktycznych, zaproponowano cztery najbardziej używane i przydatne w technice układy aksonometryczne. Na rys. 1.4_3 przedstawiono praktyczne układy aksonometryczne o następujących parametrach wynikających z rzutowania równoległego: a) układ dimetrii kawalerskiej $({\lambda }_x=1:2,{\lambda }_y=1:1,{\lambda }_z=1:1)$, b) układ dimetrii wojskowej $({\lambda }_{x^{\prime }}=1:1,{\lambda }_{y^{\prime }}=1:1,{\lambda }_{z^{\prime }}=1:2)$, c) układ izometrii równokątnej $({\lambda }_x=1:1,{\lambda }_y=1:1,{\lambda }_z=1:1)$, d) układ dimetrii prawie prostokątnej $({\lambda }_{x^{\prime }}=2:3,{\lambda }_{y^{\prime }}=1:1,{\lambda }_{z^{\prime }}=1:1)$. W układzie dimetrii kawalerskiej osie $y^{\prime }i{z}^{\prime }$ położone są względem siebie pod kątem $90^o$ . Oś $x^{\prime }$ tworzy kąt $135^o$ z osiami $y^{\prime }i{z}^{\prime }$. Układ umożliwia zapis bez zniekształceń w pł. $(0,y^{\prime },z^{\prime })$. W układzie dimetrii wojskowej oś $z^{\prime }$ układu jest pionowa, skrót zmniejsza wymiary w tym kierunku dwukrotnie. Osie $x^{\prime },y^{\prime }$ tworzą kąt $135^o$ z osią $z^{\prime }$. Skróty nie zmieniają wymiarów w kierunku tych osi. Układ izometrii równokątnej jest układem regularnym. Osie $x^{\prime },y^{\prime },z^{\prime }$ tworzą kąt $120^o$ względem siebie. Skróty nie zmieniają wymiarów w każdej osi. Tworzenie trzech pierwszych układów nie sprawia żadnych problemów. Komentarza wymaga tworzenie układu dimetrii prawie prostokątnej. Oś $z^{\prime }$ jest osią pionową. Pozostałe osie $x^{\prime }i{y}^{\prime }$ tworzymy w sposób następujący: 1. na pomocniczej linii poziomej odmierzamy osiem odcinków jednostkowych otrzymując na niej punkt, przez który prowadzimy pomocniczą prostą pionową. 2. odmierzając następnie na tej prostej w kierunku do góry 7 odcinków jednostkowych oraz 1 w dół otrzymamy dwa punkty, 3. łącząc otrzymane punkty z środkiem układu wyznaczymy położenie osi $x^{\prime }i{y}^{\prime }$. Rysowanie technicznych obiektów przestrzennych w rzutach aksonometrycznych pozwala przygotować zapis konstrukcji, który może być zrozumiały dla każdego czytelnika oraz przydatny do dalszych zapisów technicznych.

---

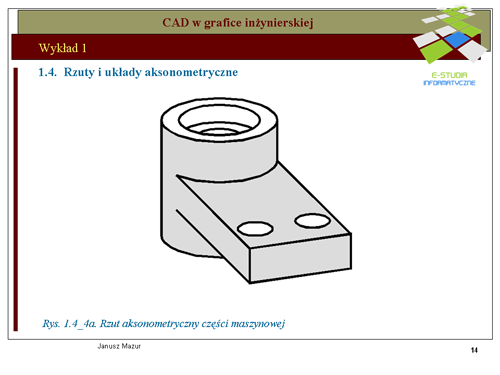
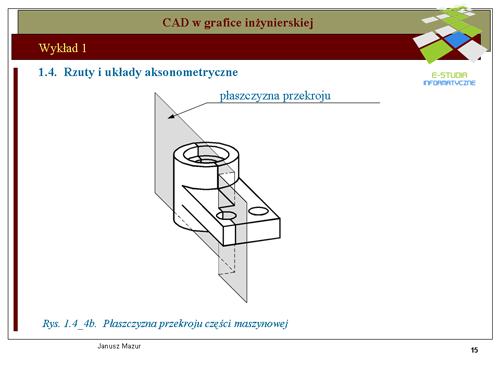
Na rys. 1.4_4a-1.4_4b przedstawiono przykład rzutu aksonometrycznego części maszynowej oraz propozycję określenia płaszczyzny przekroju bryły w zapisie prostokątnym stosowanym w technice. Zapis ten będzie przedmiotem rozważań w dalszych wykładachta.

---

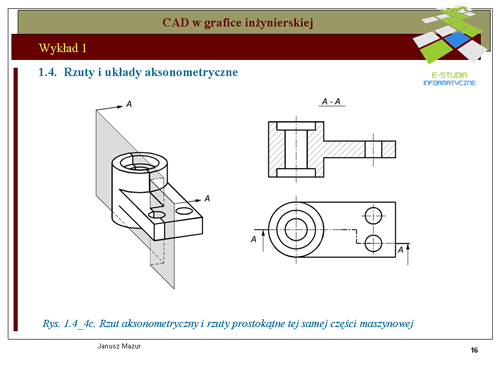
Rys. 1.4_4c przedstawia cześć maszynową w rzucie aksonometrycznym oraz zapis konstrukcji w rzutach prostokątnych. Jak widać rzut aksonometryczny ułatwia czytelnikowi identyfikację przestrzenna bryły, bez konieczności technicznej strony zapisu prostokątnego. Może stanowić pomoc dla osób o zbyt małej wyobraźni przestrzennej. Jednak rzuty prostokątne stanowią zapis, który może być przedmiotem profesjonalnych odwzorowań brył przestrzennych na płaszczyźnie.

---

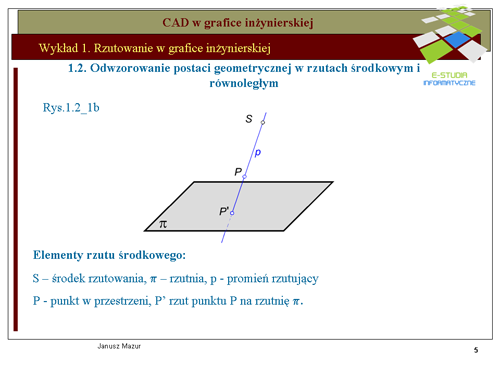
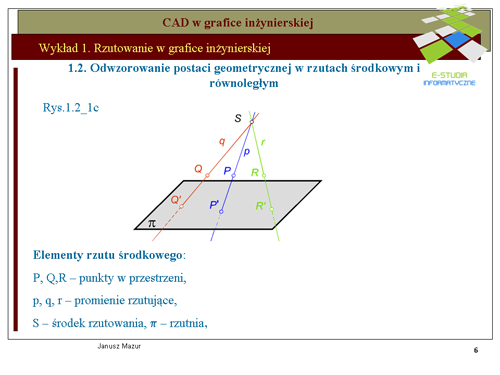
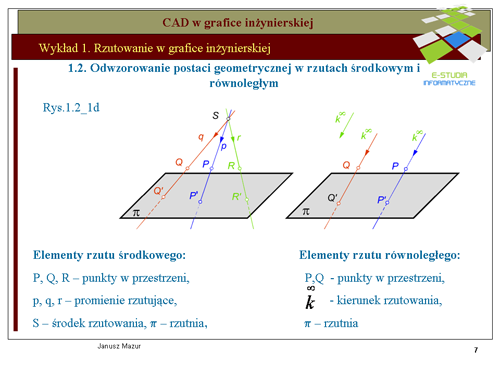
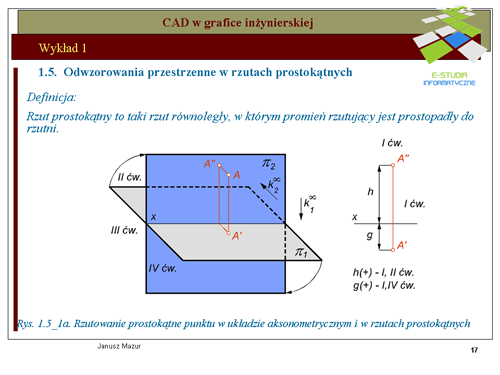
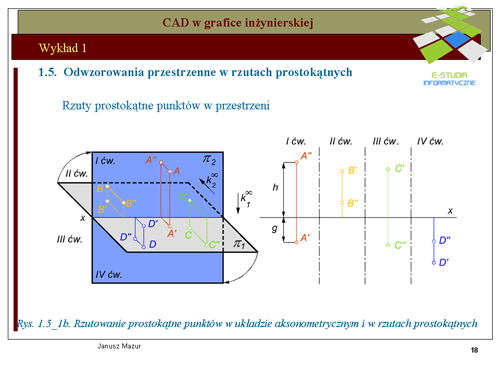
Rzutowanie prostokątne elementów przestrzennych jest podstawową formą odwzorowań stosowanych w grafice inżynierskiej. Zastosowanie trzech wzajemnie prostopadłych rzutni umożliwia jednoznaczne odwzorowanie elementów przestrzennych na płaszczyźnie i odwrotnie. Tego typu rzutowanie jest podstawą graficznego i komputerowego zapisu konstrukcji. Rzut prostokątny jest rodzajem rzutu równoległego. Zatem znane są zasady rzutowania prostokątnego. Umieszczony twór przestrzenny rzutowany jest za pomocą promieni rzutujących prostopadłych do rzutni. Na rys. rys. 1.5_1a przedstawiono zasady tworzenia rzutu prostokątnego punktu A w układzie dwu rzutni wzajemnie do siebie prostopadłych. Zasadę tworzenia rzutów prostokątnych przedstawiono również w rzutach aksonometrycznych, w celu pełniejszego zrozumienia omawianego zagadnienia. Rzutowanie prostokątne polega na generacji promieni rzutujących prostopadłych do rzutni, przez elementy tworów przestrzennych (w tym przypadku – punktu$A$)

---

Przestrzeń $E^3$ podzielona została na cztery obszary zwane ćwiartkami za pomocą dwóch przecinających się płaszczyzn - pionowej i poziomej. Płaszczyzny te po złożeniu do jednej płaszczyzny pozwalają nas jasne i jednoznaczne odwzorowania przestrzenne na płaszczyźnie rysunku. ćwiartka I jest obszarem położonym przed rzutnią pionową i nad rzutnią poziomą, ćwiartka II jest obszarem położonym za rzutnią pionową i nad rzutnią poziomą, ćwiartka III jest obszarem położonym za rzutnią pionową i pod rzutnią poziomą, ćwiartka IV jest obszarem położonym przed rzutnią pionową i pod rzutnią poziomą. Złożenie dwóch płaszczyzn do wspólnego położenia, po obrocie dookoła osi x, będącej ich krawędzią przecięcia pozwala rozmieścić rzuty na jednej wspólnej płaszczyźnie. Odległość punktu od rzutni poziomej nazywamy wysokością i oznacza się literą "h", natomiast odległość punktu od rzutni pionowej nazywamy głębokością i oznacza się "g". Wysokość jest dodatnia w ćwiartce I i II, a więc nad rzutnią poziomą, głębokość jest dodatnia w ćwiartce I i IV, a więc przed rzutnią pionową. W przypadku zaistnienia potrzeby wprowadzenia trzeciego parametru identyfikującego obiekty przestrzenne można wprowadzić trzecią rzutnię, prostopadłą do rzutni poziomej i pionowej. W tym przypadku odległość punktu od trzeciej rzutni nazywamy szerokością punktu "s".

---

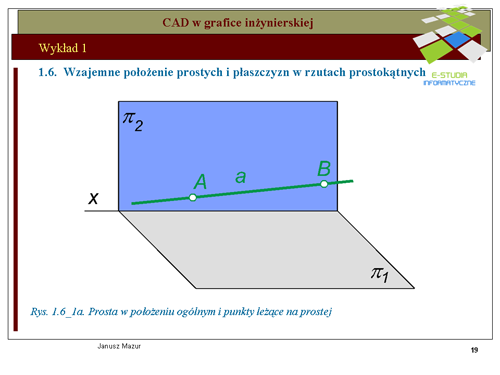
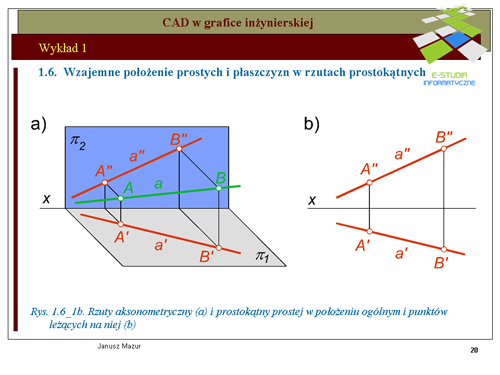
Rozważmy obecnie rzutowanie kolejnego elementu, jakim jest prosta. Prostą a można opisać jednoznacznie za pomocą dwóch punktów. Zatem rzuty prostej można wyznaczyć łącząc jednoimienne rzuty punktów A i B leżących na tej prostej. Zasady tworzenia rzutów prostej przedstawia rys.1.6_1a, 1.6_1b.

---

---

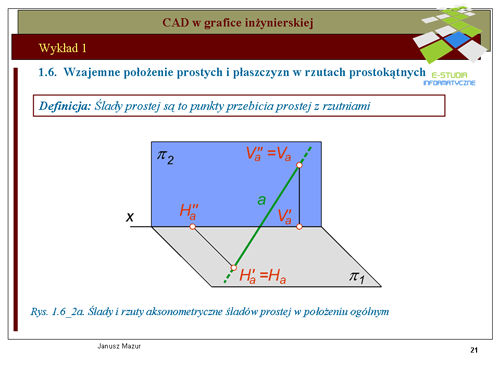
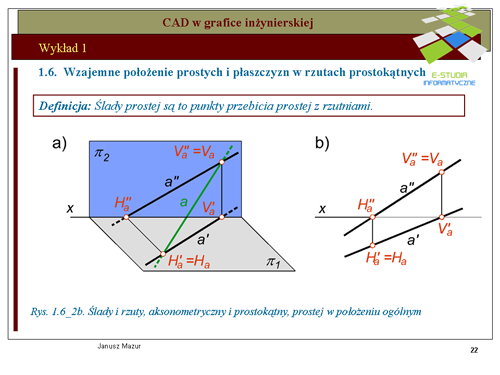
Prosta określona jednoznacznie za pomocą dwóch punktów może być określona w rzutach za pomocą rzutów punktów o szczególnym położeniu względem rzutni. Takimi punktami są ślady prostej. Śladami prostej nazywamy punkty przebicia prostej z rzutniami. Zatem możemy mówić o śladzie pionowym prostej opisywanym literą $V_a$ (od słowa vertical) oraz o śladzie poziomym $H_a$ (od słowa horizontal). Punkty $V_{a}i{H}_a$ w rzutach określone są za pomocą ich rzutów pionowych i poziomych. Rzut pionowy śladu pionowego $V{a}^{″}$ pokrywa się ze śladem pionowym natomiast rzut poziomy tego śladu $V{a}^{\prime }$ znajduje się na osi $x$ (rzuty poziome wszystkich punktów leżących na rzutni pionowej znajdują się na osi x). Rzut poziomy śladu poziomego Ha' pokrywa się ze śladem poziomym, natomiast rzut pionowy tego śladu Ha znajduje się na osi x (rzuty pionowe wszystkich punktów leżących na rzutni poziomej znajdują się na osi $x$). Rzuty prostej wraz z jej śladami przedstawiono na rys. 1.6_2a i 1.6_2b. Przedstawione rzuty prostej dotyczą jej położenia ogólnego.

---

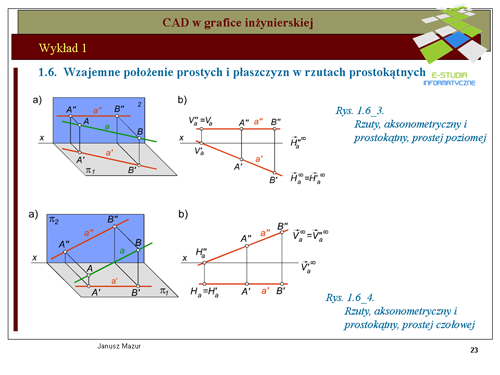
W konstrukcjach przestrzennych często wykorzystywane są inne, szczególne położenia prostych, których rzuty można łatwo przewidzieć, bez konieczności żmudnych konstrukcji pomocniczych. Do takiego położenia prostych można zaliczyć np. proste poziome (równoległe do rzutni poziomej ${\pi }_1$oraz proste czołowe (równoległe do rzutni pionowej ${\pi }_2$Rzuty prostych w położeniu szczególnym przedstawiono na rys.1.6_3 i 1.6_4. Proste szczególne charakteryzują się tym, iż jeden z rzutów jest zawsze równoległy do osi x (prostej poziomej rzut poziomy i prostej czołowej rzut pionowy). Taki parametr ułatwia realizację konstrukcji z zastosowaniem prostych szczególnych, albowiem znany jest kierunek jednego z rzutów (można pominąć konstrukcje pomocnicze wyznaczające rzuty prostej pomocniczej).

---

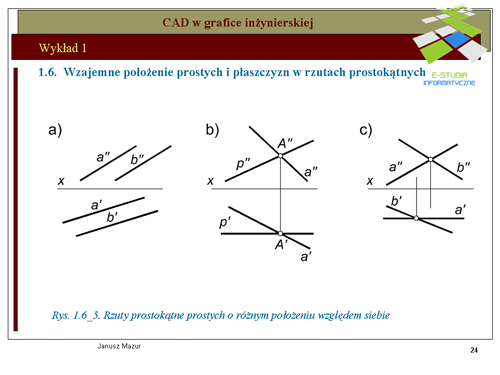
Proste w przestrzeni mogą przecinać się ze sobą, być równoległe lub być skośne względem siebie. Dwie proste przecinające się i dwie proste równoległe jednoznacznie określają płaszczyznę. W tych przypadkach mówimy, że płaszczyzna określona jest bezśladowo. Na rys. 1.6_5 przedstawiono trzy przypadki położenia dwu prostych względem siebie: a) rzuty dwu prostych równoległych b) rzuty dwu prostych przecinających się c) rzuty dwu prostych skośnych Proste (nie rzuty prostych) przedstawione na rys.1.6_5c nie przecinają się ze sobą. Punkty przecięcia rzutów nie leżą na jednej odnoszącej prostopadłej do osi x (patrz linie odniesieniowe), a więc proste nie tworzą płaszczyzny.

---

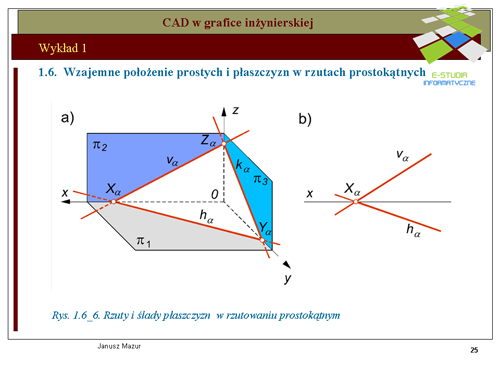
Płaszczyzny odwzorowywane są w rzutach prostokątnych w sposób umowny. Nie budzą żadnych wątpliwości płaszczyzny określone bezśladowo (tak jak przedstawione na rys. rys. 1.6_5a i 1.6_5b). Jednak ogólnie ujmując zagadnienie należy stwierdzić, iż rzutem płaszczyzny jest płaszczyzna. Zapis w tym przypadku byłby utrudniony. Płaszczyzna również może być określona za pomocą śladów - pionowego v i poziomego h. Ślady w tym przypadku są krawędziami przecięcia się płaszczyzny z rzutniami pionową i poziomą. Ilustracje odwzorowania płaszczyzny dowolnej w rzutach prostokątnych za pomocą śladów przedstawiono na rys. 1.6_6.

---

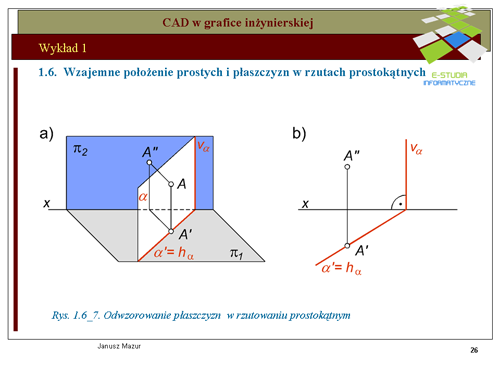
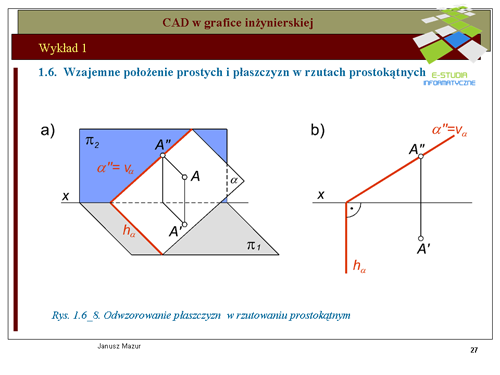
Duże znaczenie w rozwiązywaniu konstrukcji geometrycznych mają płaszczyzny o szczególnym położeniu względem rzutni. Do płaszczyzn tych należą: płaszczyzna poziomo-rzutująca i płaszczyzna pionowo-rzutująca, przedstawione na rys. rys. 1.6_7 i 1.6_8. Są to płaszczyzny prostopadłe do rzutni. Położenie płaszczyzny poziomo - rzutującej jest niezwykle interesujące z punktu widzenia realizacji konstrukcji złożonych. Wszystkie elementy płaskie znajdujące się w tej płaszczyźnie odwzorowują się w rzucie poziomym na ślad poziomy płaszczyzny, (czyli w tym przypadku na rzut poziomy płaszczyzny). Umożliwia to w szybki sposób przewidzieć położenie tych rzutów, bez konieczności stosowania konstrukcji pomocniczych. Podobnie sytuacja przedstawia się z płaszczyzną pionowo-rzutującą. Wszystkie elementy płaskie znajdujące się w tej płaszczyźnie odwzorowują się w rzucie pionowym na ślad pionowy płaszczyzny, (czyli na rzut pionowy płaszczyzny). Konstruktorzy chętnie posługują się płaszczyznami poziomo - rzutującymi i pionowo - rzutującymi. Konstrukcje stają się wtedy mniej pracochłonne.

---

Zaprezentowany wykład przedstawia podstawowe zasady odwzorowań przestrzennych stosowanych w technice. Omówiono stosowane w grafice inżynierskiej rzutowanie środkowe i równoległe. Szczególnie zwrócono uwagę na dwa rodzaje rzutu równoległego: rzut aksonometryczny i prostokątny. Rzut aksonometryczny, coraz częściej stosowany w praktyce handlowej i komercyjnej umożliwia dostęp do przestrzennych obiektów dla szerokiego grona ludzi o znikomym wykształceniu technicznym. Rzuty prostokątne stanowią możliwość zastosowania grafiki inżynierskiej w profesjonalnym, graficznym zapisie konstrukcji, pozwalają porozumiewać się inżynierom i technikom w zrozumiałym dla nich języku odwzorowań elementów przestrzennych na płaszczyźnie rysunku projektowego. W wykładzie zapoznano słuchaczy z rzutowaniem prostokątnym podstawowych elementów przestrzennych, jakimi są punkt, prosta i płaszczyzna. Elementy te stanowią podstawę złażonych konstrukcji technicznych, które powinny być zapisane w profesjonalnej grafice inżynierskiej.

---