CWGI Moduł 1: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 136: | Linia 136: | ||
|valign="top" width="500px"|[[Grafika:CWGI_M1_Slajd13.png]] | |valign="top" width="500px"|[[Grafika:CWGI_M1_Slajd13.png]] | ||
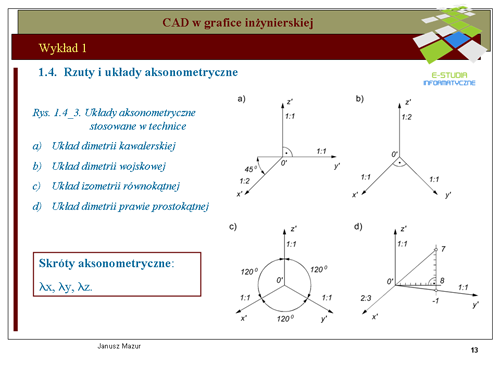
|valign="top"| Dla potrzeb graficznego zapisu konstrukcji, w wyniku doświadczeń praktycznych, zaproponowano cztery najbardziej używane i przydatne w technice układy aksonometryczne. Na rys. 1.4_3 przedstawiono praktyczne układy aksonometryczne o następujących parametrach wynikających z rzutowania równoległego: | |valign="top"| Dla potrzeb graficznego zapisu konstrukcji, w wyniku doświadczeń praktycznych, zaproponowano cztery najbardziej używane i przydatne w technice układy aksonometryczne. Na rys. 1.4_3 przedstawiono praktyczne układy aksonometryczne o następujących parametrach wynikających z rzutowania równoległego: | ||
a) układ dimetrii kawalerskiej <math>(\lambda_x=1:2, | |||
b) układ dimetrii wojskowej ( | a) układ dimetrii kawalerskiej <math>(\lambda_x=1:2, \lambda_y=1:1, \lambda_z=1:1)</math>, | ||
c) układ izometrii równokątnej ( | |||
d) układ dimetrii prawie prostokątnej ( | b) układ dimetrii wojskowej <math>(\lambda_{x'}=1:1, \lambda_{y'}=1:1, \lambda_{z'}=1:2)</math>, | ||
W układzie dimetrii kawalerskiej osie y' i z' położone są względem siebie pod kątem | |||
W układzie dimetrii wojskowej oś z' układu jest pionowa, skrót zmniejsza wymiary w tym kierunku dwukrotnie. Osie x', y' tworzą kąt | c) układ izometrii równokątnej <math>(\lambda_x =1:1, \lambda_y=1:1, \lambda_z=1:1)</math>, | ||
Układ izometrii równokątnej jest układem regularnym. Osie x', y', z' tworzą kąt | |||
Tworzenie trzech pierwszych układów nie sprawia żadnych problemów. Komentarza wymaga tworzenie układu dimetrii prawie prostokątnej. Oś z' jest osią pionową. Pozostałe osie x' i y' tworzymy w sposób następujący: | d) układ dimetrii prawie prostokątnej <math>(\lambda_{x'}=2:3, \lambda_{y'}=1:1, \lambda_{z'}=1:1)</math>. | ||
W układzie dimetrii kawalerskiej osie <math>y' i z'</math> położone są względem siebie pod kątem <math>90^o\,</math> . Oś <math>x'\,</math> tworzy kąt <math>135^o</math> z osiami <math>y' i z'</math>. Układ umożliwia zapis bez zniekształceń w pł. <math>(0, y', z')</math>. | |||
W układzie dimetrii wojskowej oś <math>z'\,</math> układu jest pionowa, skrót zmniejsza wymiary w tym kierunku dwukrotnie. Osie <math>x', y'</math> tworzą kąt <math>135^o\,</math> z osią <math>z'\,</math>. Skróty nie zmieniają wymiarów w kierunku tych osi. | |||
Układ izometrii równokątnej jest układem regularnym. Osie <math>x', y', z'</math> tworzą kąt <math>120^o</math> względem siebie. Skróty nie zmieniają wymiarów w każdej osi. | |||
Tworzenie trzech pierwszych układów nie sprawia żadnych problemów. Komentarza wymaga tworzenie układu dimetrii prawie prostokątnej. Oś <math>z'\,</math> jest osią pionową. Pozostałe osie <math>x' i y'</math> tworzymy w sposób następujący: | |||
1. na pomocniczej linii poziomej odmierzamy osiem odcinków jednostkowych otrzymując na niej | 1. na pomocniczej linii poziomej odmierzamy osiem odcinków jednostkowych otrzymując na niej | ||
punkt, przez który prowadzimy pomocniczą prostą pionową. | |||
2. odmierzając następnie na tej prostej w kierunku do góry 7 odcinków jednostkowych oraz 1 w dół | 2. odmierzając następnie na tej prostej w kierunku do góry 7 odcinków jednostkowych oraz 1 w dół | ||
otrzymamy dwa punkty, | |||
3. łącząc otrzymane punkty z środkiem układu wyznaczymy położenie osi x' i y'. | |||
3. łącząc otrzymane punkty z środkiem układu wyznaczymy położenie osi <math>x' i y'</math>. | |||
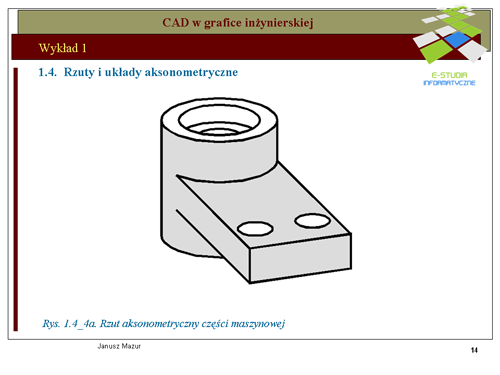
Rysowanie technicznych obiektów przestrzennych w rzutach aksonometrycznych pozwala przygotować zapis konstrukcji, który może być zrozumiały dla każdego czytelnika oraz przydatny do dalszych zapisów technicznych. | Rysowanie technicznych obiektów przestrzennych w rzutach aksonometrycznych pozwala przygotować zapis konstrukcji, który może być zrozumiały dla każdego czytelnika oraz przydatny do dalszych zapisów technicznych. | ||
Wersja z 11:29, 7 sie 2006