CWGI Moduł 1: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 45: | Linia 45: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:CWGI_M1_Slajd5.png]] | |valign="top" width="500px"|[[Grafika:CWGI_M1_Slajd5.png]] | ||
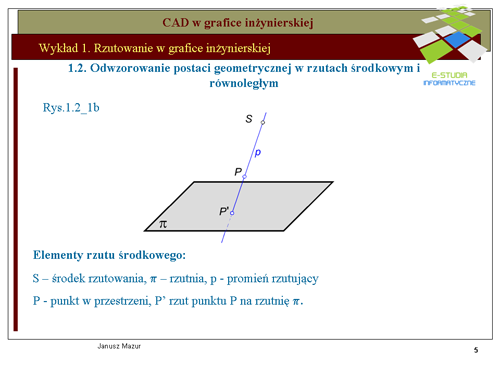
|valign="top"|Rzut środkowy punktu <math>P\,</math> otrzymano prowadząc promień rzutujący <math>p\,</math>, wychodzący ze środka rzutowania <math>S\,</math> i przechodzący przez ten punkt, aż do przecięcia się z rzutnią <math>\pi</math>Punkt przebicia promienia rzutującego z rzutnią <math>( | |valign="top"|Rzut środkowy punktu <math>P\,</math> otrzymano prowadząc promień rzutujący <math>p\,</math>, wychodzący ze środka rzutowania <math>S\,</math> i przechodzący przez ten punkt, aż do przecięcia się z rzutnią <math>\pi</math>Punkt przebicia promienia rzutującego z rzutnią <math>( P')</math> wyznacza rzut środkowy tego punktu. | ||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:CWGI_M1_Slajd6.png]] | |||
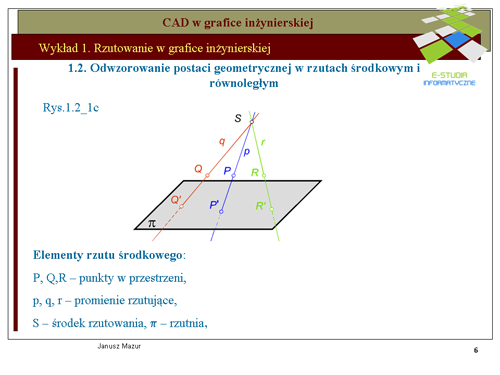
|valign="top"|Podobnie można wyznaczyć rzuty środkowe innych punktów w przestrzeni, np. punktów <math>Q i R</math>, prowadząc odpowiednie promienie rzutujące <math>q i r</math> do przecięcia się z płaszczyzną rzutni <math>\pi \,</math>. | |||
Jak widać na rysunku odwzorowanie tego typu nie jest jednoznaczne. Punktowi w przestrzeni odpowiada jeden i tylko jeden rzut punktu na rzutni <math>\pi \,</math>, lecz rzutowi punktu odpowiada nieskończenie wiele punktów leżących w przestrzeni na promieniu rzutującym. Oznacza to potrzebę wprowadzenia dalszych parametrów, które zapewniałyby tą jednoznaczność, co jest warunkiem koniecznym poprawnej identyfikacji obiektów przestrzennych. | |||
|} | |||
<hr width="100%"> | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:CWGI_M1_Slajd7.png]] | |||
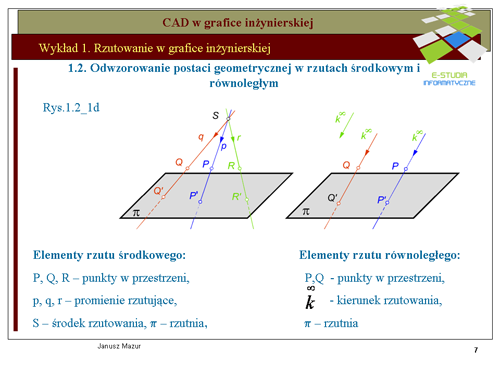
|valign="top"|W przypadku rzutu równoległego postępujemy podobnie. Jednak promienie rzutujące są równoległe do zadanego kierunku rzutowania k. Rozważając w geometrii zasady rzutowania równoległego często mamy do czynienia z '''elementami niewłaściwymi''', które zdefiniujemy dla zrozumienia zapisów umownych stosowanych w rzutowaniu. | |||
W geometrii euklidesowej dwie proste leżące na płaszczyźnie przecinają się lub są równoległe. Prosta nie leżąca w płaszczyźnie przebija ją lub jest do niej równoległa. Rozważania byłyby prostsze, gdyby dwie proste leżące w płaszczyźnie zawsze przecinały się, zaś prosta zawsze przebijała płaszczyznę. Wprowadzając określenie '''punktu niewłaściwego''' możemy uzyskać takie własności podstawowych elementów przestrzennych Do zbioru punktów właściwych, leżących na prostej dołączymy, zatem jeden punkt niewłaściwy w taki sposób, aby: | |||
*proste równoległe miały wspólny punkt niewłaściwy, | |||
*proste nierównoległe miały różne punkty niewłaściwe. | |||
Można, zatem powiedzieć, iż proste równoległe "przecinają się" w jednym punkcie niewłaściwym. Podobne rozumowanie możemy przeprowadzić w stosunku do dwóch płaszczyzn równoległych, które mieć będą wówczas "wspólną" krawędź przecięcia, zwaną prostą niewłaściwą. Punkty niewłaściwe oznaczać będziemy symbolem punktu właściwego ze znakiem "nieskończoność": | |||
: np. A:, B:, ... | |||
Prostą niewłaściwą opisujemy przy pomocy odcinka prostej zakończonego strzałką, określającego kierunek prostej łącznie z symbolem punktu niewłaściwego tzn.: | |||
<math>k^{\infty ^\rightarrow}</math> | |||
|} | |} | ||
<hr width="100%"> | <hr width="100%"> | ||