PEE Zadania do samodzielengo rozwiązania: Różnice pomiędzy wersjami
Nie podano opisu zmian |
m Zastępowanie tekstu – „\</math>” na „\ </math>” |
||
| (Nie pokazano 36 wersji utworzonych przez 3 użytkowników) | |||
| Linia 9: | Linia 9: | ||
Dane: | Dane: | ||
<math>R_1=3\Omega</math> | : <math>R_1=3\Omega</math> | ||
<math>R_2=7\Omega</math> | : <math>R_2=7\Omega</math> | ||
<math>R_3=20\Omega</math> | : <math>R_3=20\Omega</math> | ||
<math>R_4=5\Omega</math> | : <math>R_4=5\Omega</math> | ||
<math>R_5 | : <math>R_5=10\Omega</math> | ||
: <math>R_6=10\Omega</math> | |||
: | |||
Odp. <math>R_{AB}=5,26\Omega</math> | Odp. <math>R_{AB}=5,26\Omega</math> | ||
| Linia 36: | Linia 36: | ||
Dane: | Dane: | ||
<math>R_1=2\Omega</math> | : <math>R_1=2\Omega</math> | ||
<math>R_2=5\Omega</math> | : <math>R_2=5\Omega</math> | ||
<math>R_3=1\Omega</math> | : <math>R_3=1\Omega</math> | ||
<math>R_4=3\Omega</math> | : <math>R_4=3\Omega</math> | ||
<math>R_5=2\Omega</math> | : <math>R_5=2\Omega</math> | ||
<math>R_6=1\Omega</math> | : <math>R_6=1\Omega</math> | ||
<math>R_7=1\Omega</math> | : <math>R_7=1\Omega</math> | ||
<math>R_8=2\Omega</math> | : <math>R_8=2\Omega</math> | ||
| Linia 56: | Linia 56: | ||
<hr width="100%"> | <hr width="100%"> | ||
'''Zad. 3''' | |||
Metodą praw Kirchhoffa obliczyć prądy w obwodzie. | |||
a) | |||
[[Grafika:PEE_Zadania_do_sam_3.jpg]] | |||
Dane: | |||
: <math>I=5A\ </math>, | |||
: <math>E=10V\ </math>, | |||
: <math>R_1=1\Omega</math> | |||
: <math>R_2=5\Omega</math> | |||
: <math>R_3=10\Omega</math> | |||
Odp. <math>I_1=4A\ </math>,, <math>I_2=1A\ </math>, | |||
<hr width="100%"> | |||
'''Zad. 4''' | |||
Wyznaczyć rozpływy prądów w obwodzie. Sporządzić bilans mocy. | |||
a) | |||
[[Grafika:PEE_Zadania_do_sam_4.jpg]] | |||
Dane: | |||
: <math>e(t)=10\sqrt{2}sin(t+90^\circ)\, V</math> | |||
: <math>R_1=2\Omega</math> | |||
: <math>R_2=1\Omega</math> | |||
: <math>C=0,5F\ </math>, | |||
: <math>L=1H\ </math>, | |||
Odp. <math>I=(0,5+j3,5)\, A</math>, <math>U_{RLC}=(-1+j3)\, A</math>, <math>I_1=(9+j1)\, A</math>, <math>I_2=(-1,5-j0,1)\, A</math>, <math>I_3=(-1+j3)\, A</math>, | |||
<math>P_{odb}=35\, W</math>, <math>Q_{odb}=5\, var</math>, <math>S_{gen}=(35+j5)\, VA</math> | |||
<hr width="100%"> | |||
'''Zad. 5''' | |||
Narysować wykres wektorowy dla obwodu. | |||
a) | |||
[[Grafika:PEE_Zadania_do_sam_5.jpg]] | |||
<hr width="100%"> | |||
'''Zad. 6''' | |||
Obliczyć prądy w obwodach stosując metodę: | |||
a) potencjałów węzłowych | |||
[[Grafika:PEE_Zadania_do_sam_6.jpg]] | |||
Dane: | |||
: <math>I_1=5\, A</math> | |||
: <math>I_2=2\, A</math> | |||
: <math>E=10\, V</math> | |||
: <math>R_1=5\Omega</math> | |||
: <math>R_2=5\Omega</math> | |||
: <math>R_3=5\Omega</math> | |||
: <math>R_4=10\Omega</math> | |||
Odp. <math>I_{R2}=2,75\, A</math>, <math>I_{R3}=2,25\, A</math>, <math>I_{R4}=0,75\, A</math> | |||
b) metodę oczkową | |||
[[Grafika:PEE_Zadania_do_sam_7.jpg]] | |||
Dane: | |||
: <math>I_1=5\, A</math> | |||
: <math>I_2=10\, A</math> | |||
: <math>R_1=1\Omega</math> | |||
: <math>R_2=2\Omega</math> | |||
: <math>R_3=2\Omega</math> | |||
: <math>R_4=8\Omega</math> | |||
: <math>R_4=3\Omega</math> | |||
Odp. <math>I_{R2}=-7\, A</math>, <math>I_{R3}=3\, A</math>, <math>I_{R4}=2\, A</math>, <math>I_{R5}=8\, A</math> | |||
<hr width="100%"> | |||
'''Zad. 7''' | |||
Stosując metodę Thevenina wyznaczyć prąd <math>I_x\ </math>, w obwodzie. | |||
[[Grafika:PEE_Zadania_do_sam_8.jpg]] | |||
Dane: | |||
: <math>E_1=20\, V</math> | |||
: <math>E_2=5\, V</math> | |||
: <math>R_1=10\Omega</math> | |||
: <math>R_2=20\Omega</math> | |||
: <math>R_3=10\Omega</math> | |||
: <math>R_4=10\Omega</math> | |||
: <math>R_5=5\Omega</math> | |||
Odp. <math>I_x=0,5\, A</math> | |||
<hr width="100%"> | |||
'''Zad. 8''' | |||
Obliczyć prądy i bilans mocy w obwodzie. | |||
a) | |||
[[Grafika:PEE_Zadania_do_sam_9.jpg]] | |||
Dane: | |||
: <math>i(t)=10\sqrt{2}sin(t+45^\circ)\, A</math> | |||
: <math>R=5\Omega</math> | |||
: <math>L_1=2H\ </math>, | |||
: <math>L_2=1H\ </math>, | |||
: <math>C_1=0,5F\ </math>, | |||
: <math>C_2=0,5F\ </math>, | |||
Odp. <math>I_1=(2,72+j4,08)\, A\;\;</math>, <math>I_2=(-2,72-j4,08)\, A\;\;</math>, <math>I_3=(1,67-j1,09)\, A\;\;</math>, <math>I_4=(5,44+j8,16)\, A\;\;</math>, <math>P_{odb}=19,225\, W\;\;</math>, <math>Q_{odb}=-96,125\, var\;\;</math>, <math>S_{gen}=(19,225-j96,125)\, VA</math>. | |||
<hr width="100%"> | |||
'''Zad. 9''' | |||
Wyeliminować sprzężenia w obwodzie. | |||
a) | |||
[[Grafika:PEE_Zadania_do_sam_10.jpg]] | |||
Odp. | |||
[[Grafika:PEE_Zadania_do_sam_11.jpg]] | |||
<hr width="100%"> | |||
'''Zad. 10''' | |||
Obliczyć rozpływy prądów w obwodzie, napięcia na cewkach sprzężonych oraz sporządzić bilans mocy. | |||
[[Grafika:PEE_Zadania_do_sam_12.jpg]] | |||
Dane: | |||
: <math>e(t)=100\sqrt{2}sin \omega t</math> | |||
: <math>R_1=10\Omega</math> | |||
: <math>R_2=5\Omega</math> | |||
: <math>X_{L1}=25\Omega</math>, <math>X_{L2}=40\Omega</math>, <math>X_M=10\Omega</math>, | |||
Odp. <math>I=(3,19-j8,03)\, A</math>, <math>I_1=(2,2-j4,52)\, A</math>, <math>I_2=(0,99-j3,51)\, A</math>, <math>U_{L1}=(77,96+j45,21)\, V</math>, <math>U_{L2}=(95,05+j17,53)\, V</math>, <math>P_{odb}=319,35\, W</math>, <math>Q_{odb}=802,76\, var</math>, <math>S_{źr}=(319,35+j802,76)\, VA</math> | |||
<hr width="100%"> | |||
'''Zad. 11''' | |||
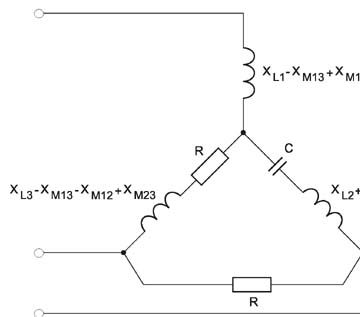
Obliczyć moduły prądów liniowych odbiornika trójfazowego przedstawionego na rysunku. | |||
[[Grafika:PEE_Zadania_do_sam_13.jpg]] | |||
Dane: | |||
: <math>R=10\Omega</math> | |||
: <math>X_C=10\Omega</math> | |||
: <math>X_M=10\Omega</math> | |||
: <math>X_{L1}=20\Omega</math> | |||
: <math>X_{L2}=20\Omega</math> | |||
Odp. <math>|I_A|=34,5\, A</math>, <math>|I_B|=24\, A</math>, <math>|I_C|=36,8\, A</math> | |||
<hr width="100%"> | |||
'''Zad. 12''' | |||
Wyznaczyć opis stanowy obwodu. | |||
[[Grafika:PEE_Zadania_do_sam_14.jpg]] | |||
Dane: | |||
: <math>R_1=2\Omega</math> | |||
: <math>R_2=1\Omega</math> | |||
: <math>L_1=1H\ </math>, | |||
: <math>L_2=2H\ </math>, | |||
: <math>M=1H\ </math>, | |||
: <math>C=1F\ </math>, | |||
:<math>y= | |||
\begin{bmatrix} | |||
i_{R_1}\\ | |||
i_C\\ | |||
u_i | |||
\end{bmatrix} | |||
</math> | |||
Odp. | |||
:<math> | |||
\begin{bmatrix} | |||
\frac{di_{L1}}{dt}\\ \frac{di_{L2}}{dt} \\ \frac{du_C}{dt} \end{bmatrix}= | |||
\begin{bmatrix} | |||
2 & -1 & -1 \\4 & -1 & -1 \\ 0 & 1 & 0 | |||
\end{bmatrix} | |||
\begin{bmatrix} | |||
i_{L1} \\ i_{L2} \\ u_C | |||
\end{bmatrix}+ | |||
\begin{bmatrix} | |||
1 & 1 \\ 2 & 1 \\ 0 & 0 | |||
\end{bmatrix} | |||
\begin{bmatrix} | |||
e \\ i | |||
\end{bmatrix} | |||
</math> | |||
:<math> | |||
\begin{bmatrix} | |||
i_{R_1}\\i_C \\ u_i \end{bmatrix}= | |||
\begin{bmatrix} | |||
1 & 0 & 0 \\0 & 1 & 0 \\ 0 & -1 & 0 | |||
\end{bmatrix} | |||
\begin{bmatrix} | |||
i_{L1} \\ i_{L2} \\ u_C | |||
\end{bmatrix}+ | |||
\begin{bmatrix} | |||
0 & 0 \\ 0 & 0 \\ 0 & 1 | |||
\end{bmatrix} | |||
\begin{bmatrix} | |||
e \\ i | |||
\end{bmatrix} | |||
</math> | |||
<hr width="100%"> | |||
'''Zad. 13''' | |||
Wyznaczyć i narysować przebieg <math>i_L(t)</math> w stanie nieustalonym po przełączeniu w obwodzie. | |||
[[Grafika:PEE_Zadania_do_sam_15.jpg]] | |||
Dane: | |||
: <math>e_1(t)=10\sqrt{2}sin(\omega t-90^\circ)\, V</math> | |||
: <math>e_2(t)=5\, V</math> | |||
: <math>R=5\Omega</math> | |||
: <math>L=1H\ </math>, | |||
: <math>C=0,5F\ </math>, | |||
Odp. <math>i_L(t)=1+1,86\sqrt{2}sin(\omega t-111,8^\circ)-1,17e^{-2,5t}</math> | |||
<hr width="100%"> | |||
'''Zad. 14''' | |||
Określić oraz narysować przebieg prądu oraz napięcia kondensatora w stanie nieustalonym po załączeniu wyłącznika. Kondensator był wstępnie naładowany do napięcia <math>u_C(0^{-}</math>. | |||
[[Grafika:PEE_Zadania_do_sam_16.jpg]] | |||
Dane: | |||
: <math>i=10A\ </math>, | |||
: <math>u_C(0^{-})=20\, V</math> | |||
: <math>R=10\Omega</math> | |||
: <math>L=5H\ </math>, | |||
: <math>C=\frac{1}{5}F\ </math>, | |||
Odp. | |||
: <math>u_C(t)=100-80^{-t}-80t^{-t}\ </math>, | |||
: <math>i_C(t)=80t^{-t}\ </math>, | |||
<hr width="100%"> | |||
'''Zad. 15''' | |||
Wyznaczyć transmitancje napięciowe obwodu oraz charakterystyki częstotliwościowe. | |||
a) | |||
[[Grafika:PEE_Zadania_do_sam_17.jpg]] | |||
Dane: | |||
: <math>R=1k\Omega</math> | |||
: <math>C=1\mu F\ </math>, | |||
Odp. | |||
: <math>H(s)=\frac{s}{s+1000}</math> | |||
: <math>|H(j\omega)|=\frac{\omega}{\sqrt{\omega^2+10^6}}</math> | |||
: <math>\varphi(\omega)=90^\circ-arctg\left(\frac{\omega}{1000} \right)</math> | |||
<hr width="100%"> | |||
'''Zad. 16''' | |||
Wyznaczyć transmitancję napięciową oraz odpowiedź impulsową obwodu. | |||
a) | |||
[[Grafika:PEE_Zadania_do_sam_18.jpg]] | |||
Dane: | |||
: <math>R=1\Omega</math> | |||
: <math>L=1H\ </math>, | |||
: <math>C=1F\ </math>, | |||
Odp. | |||
: <math>T(s)=\frac{1}{s^2+s+1}</math> | |||
: <math>h(t)=\frac{2}{\sqrt{3}}e^{-0,5t}sin\sqrt{\frac{3}{4}}t</math> | |||
<hr width="100%"> | |||
'''Zad. 17''' | |||
Wyznaczyć opis admitancyjny obwodu | |||
a) | |||
[[Grafika:PEE_Zadania_do_sam_19.jpg]] | |||
Odp. | |||
:<math> | |||
\begin{bmatrix} | |||
I_1\\I_2 \end{bmatrix}= | |||
\begin{bmatrix} | |||
Y_1+Y_3+kY_3 & -Y_3-kY_3 \\-Y_3-kY_3 & Y_2+Y_3+kY_3 | |||
\end{bmatrix} | |||
\begin{bmatrix} | |||
U_1 \\ U_2 | |||
\end{bmatrix} | |||
</math> | |||
<hr width="100%"> | |||
'''Zad. 18''' | |||
Obliczyć impedancję wejściową dla obwodów | |||
a) | |||
[[Grafika:PEE_Zadania_do_sam_20.jpg]] | |||
Odp. | |||
: <math>Z_{we}(s)=\frac{s{R_ź}^2C_1}{1+s^2{R_ź}^2C_1C_2}</math> | |||
b) | |||
[[Grafika:PEE_Zadania_do_sam_21.jpg]] | |||
Odp. | |||
: <math>Z_{we}=Z_1-Z_2</math> | |||
<hr width="100%"> | |||
'''Zad. 19''' | |||
W temperaturze <math>27 ^oC</math> koncentracja swobodnych elektronów w płytce krzemowej jest równa <math>n_{i0} = 1,5·10^{16} m^{-3}</math>. Ile razy wzrośnie koncentracja ładunku swobodnego, jeżeli temperatura wzrośnie o <math>100 K</math>. Dane: szerokość pasma zabronionego <math>1,12 eV</math>, w <math>1 m3</math> jest <math>4,99·10^{28}</math> atomów krzemu, stała <math>k = 1,38·10^{-23} J/K</math>. | |||
Odp. | |||
: <math>1,17·10^{5}</math> razy. | |||
<hr width="100%"> | |||
'''Zad. 20''' | |||
Stała dyfuzji elektronów w temperaturze <math>27 ^oC</math> dla krzemu jest równa <math>D_n = 35·10^{-4} m^2s^{-1}</math>, | |||
a czas życia nośników <math>\tau = 10^{-4} s</math>. Obliczyć drogę dyfuzji. | |||
Odp. | |||
: 0,592 mm | |||
<hr width="100%"> | |||
'''Zad. 21''' | |||
Dla tranzystora bipolarnego przy <math>I_C = 3 mA</math> i <math>U_{CE} = 5 V</math> rezystancja <math>r_{CE} = 40 k\Omega</math>, <math>\beta_0 = 150</math>. obliczyć wartości parametrów <math>\beta_Z</math>, <math>U_E</math> modelujących zjawisko Earlyego. | |||
Odp. | |||
: <math>\beta_Z = 143,7</math> | |||
: <math>U_E = 115 V</math> | |||
<hr width="100%"> | |||
'''Zad. 22''' | |||
Dla układu zasilania tranzystora bipolarnego przedstawionego na rysunku wyznaczyć współczynniki stabilizacji punktu pracy. Dane: <math>E_C</math>, <math>E_B</math>, <math>R_C</math>, <math>R_B</math>, <math>R_E</math>, <math>U_{BE}</math>, <math>I_{CB0}</math>, <math>\beta</math>. | |||
[[Grafika:PEE_Zadania_do_sam_22a.jpg]] | |||
Odp. | |||
: [[Grafika:PEE_Zadania_do_sam_22b.jpg]] | |||
<hr width="100%"> | |||
'''Zad. 23''' | |||
Wyznaczyć funkcję zależności nachylenia <math>S</math> charakterystyki bramkowej tranzystora unipolarnego od prądu drenu <math>I_D</math> | |||
Odp. | |||
: [[Grafika:PEE_Zadania_do_sam_23.jpg]] | |||
<hr width="100%"> | |||
'''Zad. 24''' | |||
Ile razy zmieni się wzmocnienie napięciowe układu, jeżeli zamkniemy styki wyłącznika W. | |||
[[Grafika:PEE_Zadania_do_sam_24a.jpg]] | |||
Odp. | |||
: [[Grafika:PEE_Zadania_do_sam_24b.jpg]] | |||
Aktualna wersja na dzień 12:04, 5 wrz 2023
Przykłady zadań do samodzielengo rozwiązania
Zad 1
Obliczyć rezystancję z zacisków A-B obwodu.
Dane:
Odp.
Zad. 2
Obliczyć rezystancję z zacisków A-B obwodu.
a)
Dane:
Odp.
Zad. 3
Metodą praw Kirchhoffa obliczyć prądy w obwodzie.
a)
Dane:
- ,
- ,
Odp. ,, ,
Zad. 4
Wyznaczyć rozpływy prądów w obwodzie. Sporządzić bilans mocy.
a)
Dane:
- ,
- ,
Odp. , , , , ,
, ,
Zad. 5
Narysować wykres wektorowy dla obwodu.
a)
Zad. 6
Obliczyć prądy w obwodach stosując metodę:
a) potencjałów węzłowych
Dane:
Odp. , ,
b) metodę oczkową
Dane:
Odp. , , ,
Zad. 7
Stosując metodę Thevenina wyznaczyć prąd , w obwodzie.
Dane:
Odp.
Zad. 8
Obliczyć prądy i bilans mocy w obwodzie.
a)
Dane:
- ,
- ,
- ,
- ,
Odp. , , , , , , .
Zad. 9
Wyeliminować sprzężenia w obwodzie.
a)
Odp.
Zad. 10
Obliczyć rozpływy prądów w obwodzie, napięcia na cewkach sprzężonych oraz sporządzić bilans mocy.
Dane:
- , , ,
Odp. , , , , , , , Parser nie mógł rozpoznać (błąd składni): {\displaystyle S_{źr}=(319,35+j802,76)\, VA}
Zad. 11
Obliczyć moduły prądów liniowych odbiornika trójfazowego przedstawionego na rysunku.
Dane:
Odp. , ,
Zad. 12
Wyznaczyć opis stanowy obwodu.
Dane:
- ,
- ,
- ,
- ,
Odp.
Zad. 13
Wyznaczyć i narysować przebieg w stanie nieustalonym po przełączeniu w obwodzie.
Dane:
- ,
- ,
Odp.
Zad. 14
Określić oraz narysować przebieg prądu oraz napięcia kondensatora w stanie nieustalonym po załączeniu wyłącznika. Kondensator był wstępnie naładowany do napięcia .
Dane:
- ,
- ,
- ,
Odp.
- ,
- ,
Zad. 15
Wyznaczyć transmitancje napięciowe obwodu oraz charakterystyki częstotliwościowe.
a)
Dane:
- ,
Odp.
Zad. 16
Wyznaczyć transmitancję napięciową oraz odpowiedź impulsową obwodu.
a)
Dane:
- ,
- ,
Odp.
Zad. 17
Wyznaczyć opis admitancyjny obwodu
a)
Odp.
Zad. 18
Obliczyć impedancję wejściową dla obwodów
a)
Odp.
- Parser nie mógł rozpoznać (błąd składni): {\displaystyle Z_{we}(s)=\frac{s{R_ź}^2C_1}{1+s^2{R_ź}^2C_1C_2}}
b)
Odp.
Zad. 19
W temperaturze koncentracja swobodnych elektronów w płytce krzemowej jest równa Parser nie mógł rozpoznać (błąd składni): {\displaystyle n_{i0} = 1,5·10^{16} m^{-3}} . Ile razy wzrośnie koncentracja ładunku swobodnego, jeżeli temperatura wzrośnie o . Dane: szerokość pasma zabronionego , w jest Parser nie mógł rozpoznać (błąd składni): {\displaystyle 4,99·10^{28}} atomów krzemu, stała Parser nie mógł rozpoznać (błąd składni): {\displaystyle k = 1,38·10^{-23} J/K} .
Odp.
- Parser nie mógł rozpoznać (błąd składni): {\displaystyle 1,17·10^{5}} razy.
Zad. 20
Stała dyfuzji elektronów w temperaturze dla krzemu jest równa Parser nie mógł rozpoznać (błąd składni): {\displaystyle D_n = 35·10^{-4} m^2s^{-1}} , a czas życia nośników . Obliczyć drogę dyfuzji.
Odp.
- 0,592 mm
Zad. 21
Dla tranzystora bipolarnego przy i rezystancja , . obliczyć wartości parametrów , modelujących zjawisko Earlyego.
Odp.
Zad. 22
Dla układu zasilania tranzystora bipolarnego przedstawionego na rysunku wyznaczyć współczynniki stabilizacji punktu pracy. Dane: , , , , , , , .
Odp.
Zad. 23
Wyznaczyć funkcję zależności nachylenia charakterystyki bramkowej tranzystora unipolarnego od prądu drenu
Odp.
Zad. 24
Ile razy zmieni się wzmocnienie napięciowe układu, jeżeli zamkniemy styki wyłącznika W.
Odp.