Matematyka dyskretna 1/Ćwiczenia 5: Współczynniki dwumianowe: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
m Zastępowanie tekstu – „.↵</math>” na „</math>” |
m Zastępowanie tekstu – „,↵</math>” na „</math>,” |
||
| Linia 20: | Linia 20: | ||
<center><math>{n\choose k}<{n\choose k+1} | <center><math>{n\choose k}<{n\choose k+1}</math>,</center> | ||
</math></center> | |||
| Linia 194: | Linia 193: | ||
<center> | <center> | ||
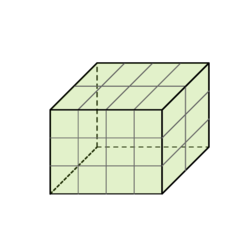
<math>\frac{m^2(m-1)}{2}+\frac{m^2(m-1)}{2}+m^2=m^3 | <math>\frac{m^2(m-1)}{2}+\frac{m^2(m-1)}{2}+m^2=m^3</math>, | ||
</math> | |||
</center> | </center> | ||
Aktualna wersja na dzień 21:50, 11 wrz 2023
Współczynniki dwumianowe
Ćwiczenie 1
Wskaż największy wyraz w -tym wierszu Trójkąta Pascala i odpowiedź uzasadnij.
Wskazówka
Rozwiązanie
Ćwiczenie 2
Posługując się interpretacją kombinatoryczną pokaż, że
Wskazówka
Rozwiązanie
Ćwiczenie 3
Posługując się interpretacją kombinatoryczną pokaż, że
Wskazówka
Rozwiązanie
Ćwiczenie 4
Posługując się interpretacją kombinatoryczną pokaż, że
Wskazówka
Rozwiązanie
Ćwiczenie 5
Posługując się interpretacją kombinatoryczną pokaż, że
Wskazówka
Rozwiązanie
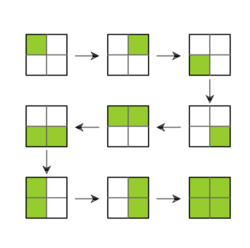
Ćwiczenie 6
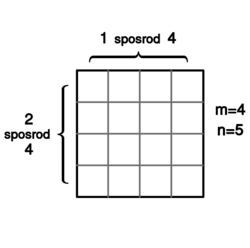
Ile prostokątów zawiera się w kratce ? Dla przykładu w kratce jest ich .
Wskazówka
Rozwiązanie
Ćwiczenie 7
Udowodnij, że:
Wskazówka
Rozwiązanie
Ćwiczenie 8
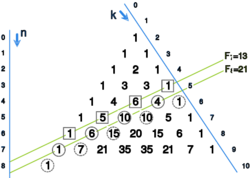
Udowodnij, że:
gdzie jest -tą liczbą Fibonacci'ego
Wskazówka
Rozwiązanie