Matematyka dyskretna 1/Ćwiczenia 12: Grafy: Różnice pomiędzy wersjami
m Zastępowanie tekstu – „ </math>” na „</math>” Znacznik: Wycofane |
m Zastępowanie tekstu – „.↵</math>” na „</math>” |
||
| (Nie pokazano 1 pośredniej wersji utworzonej przez tego samego użytkownika) | |||
| Linia 39: | Linia 39: | ||
<center> | <center> | ||
<math>v_i \triangleq v_j\quad</math> w.t.w. <math>\quad \left\vert i-j \right\vert\</math> jest wielokrotnością <math>\ 4 | <math>v_i \triangleq v_j\quad</math> w.t.w. <math>\quad \left\vert i-j \right\vert\ </math> jest wielokrotnością <math>\ 4</math> | ||
</math> | |||
</center> | </center> | ||
| Linia 167: | Linia 166: | ||
<center><math>v_1\to v_2\to\ldots\to v_r | <center><math>v_1\to v_2\to\ldots\to v_r</math></center> | ||
</math></center> | |||
| Linia 225: | Linia 223: | ||
<center><math>\left\vert \mathsf{ E}\!\left(\mathbf{G}\right) \right\vert\leq k^2+2k+1=\left( k+1 \right)^2 | <center><math>\left\vert \mathsf{ E}\!\left(\mathbf{G}\right) \right\vert\leq k^2+2k+1=\left( k+1 \right)^2</math></center> | ||
</math></center> | |||
| Linia 277: | Linia 274: | ||
<center><math>\frac{2\left( n-1 \right)+1}{2}=n-\frac{1}{2} | <center><math>\frac{2\left( n-1 \right)+1}{2}=n-\frac{1}{2}</math></center> | ||
</math></center> | |||
Aktualna wersja na dzień 21:31, 11 wrz 2023
Grafy I
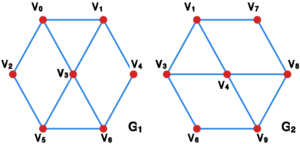
Ćwiczenie 1
Niech oraz będą grafami przedstawionymi na rysunku 1. Przedstaw sumę , przecięcie , oraz różnicę .
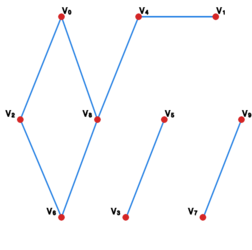
Ćwiczenie 2
Graf jest przedstawiony na rysunku 4. Przedstaw graf ilorazowy dla relacji równoważności zdefiniowanej przez:
w.t.w. jest wielokrotnością
Ćwiczenie 3
Niech będzie grafem prostym z co najmniej dwoma wierzchołkami. Wykaż, że zawiera dwa wierzchołki tego samego stopnia.
Ćwiczenie 4
Wykaż, że w grupie sześciu osób zawsze znajdą się trzy, które albo znają się nawzajem, albo żadna z nich nie zna dwóch pozostałych.
Ćwiczenie 5
Dopełnienie grafu to graf . Przedstaw dopełnienie grafu pełnego oraz dwudzielnego grafu pełnego . Przedstaw graf, którego dopełnienie jest z nim izomorficzne.
Ćwiczenie 6
Niech będzie grafem prostym, w którym każdy wierzchołek ma co najmniej sąsiadów. Wykaż, że zawiera cykl o długości co najmniej .
Ćwiczenie 7
Niech będzie grafem prostym o wierzchołkach, niezawierającym trójkątów. Wykaż, że ma co najwyżej krawędzi i podaj przykład grafu, w którym to górne oszacowanie jest osiągnięte.
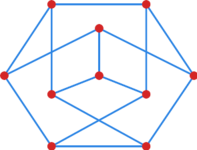
Ćwiczenie 8
Wskaż jakieś drzewo rozpinające w grafie Petersena z rysunku 6.
Prykładowe drzewo rozpinające w grafie Petersena zostało przedstawione na rysunku 7.
Ćwiczenie 9
Pokaż, że w dowolnym drzewie o co najmniej dwu wierzchołkach, istnieją co najmniej dwa wierzchołki o stopniu równym jeden.
Ćwiczenie 10
Centrum spójnego grafu to taki wierzchołek , dla którego maksymalna odległość pomiędzy i dowolnym innym wierzchołkiem grafu jest możliwie najmniejsza. Udowodnij, że każde drzewo ma albo dokładnie jedno centrum, albo dwa sąsiednie centra.