Języki, automaty i obliczenia/Ćwiczenia 7: Twierdzenie Kleene'ego. Własności języków i gramatyk regularnych

Ćwiczenia 7

Ćwiczenie 1

Niech $A=\{a,b\}$. Dla automatów${ℬ}=(S_{{ℬ}},A,f_{{ℬ}},s_{{ℬ}},F_{{ℬ}}),{𝒞}=(S_{{𝒞}},A,f_{{𝒞}},s_{{𝒞}},F_{{𝒞}})$ $S_{{ℬ}}=\{s_{{ℬ}},s_1,s_2\},F_{{ℬ}}=\{s_2\},S_{{𝒞}}=\{s_{{𝒞}},s\},F_{{𝒞}}=\{s\}$,

gdzie

$\begin{array}{cccc}{f}_{{ℬ}}& s_{{ℬ}}& s_1& s_2\\ a& s_2& s_1& s_2\\ b& s_1& s_1& s_2\end{array}\begin{array}{ccc}{f}_{{𝒞}}& s_{{𝒞}}& s\\ a& s& s\\ b& s_{{𝒞}}& s_{{𝒞}}\end{array}$ skonstruuj automat ${𝒜}$ taki, że $L({𝒜})=L({ℬ})\cap L({𝒞})$,

Rozwiązanie

$L({𝒜})=(S_{{ℬ}}\times S_{{𝒞}},A,f_{{𝒜}},(s_{{ℬ}},s_{{𝒞}}),F_{{ℬ}}\times F_{{𝒞}})$. Funkcja przejść zadana jest grafem

Rysunek 1

Zauważ, że otrzymany automat nie jest minimalny. Jakie języki akceptują automaty ${𝒜}$, ${ℬ}$ i ${𝒞}$?

Ćwiczenie 2

Niech $A=\{a,b\}$. Dla automatu ${ℬ}=(S_{{ℬ}},A,f_{{ℬ}},s_{{ℬ}},F_{{ℬ}})$,

gdzie

$S_{{ℬ}}=\{s_{{ℬ}},s_1,s_2\},F_{{ℬ}}=\{s_1\}$,

a funkcja przejść zdefiniowana jest następująco:

$\begin{array}{cccc}{f}_{{ℬ}}& s_{{ℬ}}& s_1& s_2\\ a& s_1& s_2& s_2\\ b& s_1& s_{{ℬ}}& s_1\end{array}$

skonstruuj automat deterministyczny ${𝒜}$ taki, że

$L({𝒜})=L({ℬ}{)}^{*}$.

Wskazówka

Pomocne może być użycie automatu z pustymi przejściami.

Rozwiązanie

Automat ${ℬ}$ pokazany jest na rysunku 2.

Rysunek 2

Aby skonstruować automat akceptujący język $L({ℬ}{)}^{*}$, wystarczy dodać przejście $f(s_1,1)=s_{{ℬ}}$ (dlaczego?). Automat z pustymi przejściami akceptujący $L({ℬ}{)}^{*}$ pokazany jest na rysunku 3.

Rysunek 3

Po usunięciu pustych przejść otrzymujemy automat z rysunku 4:

Rysunek 4

Teraz wystarczy skonstruować równoważny automat deterministyczny.

Ćwiczenie 3

Dane są dwa automaty nad tym samym alfabetem $A$
${𝒜}=(S,f,s_0,T)$ i ${ℬ}=(Q,g,t_0,F)$. Udowodnij, że istnieje liczba $p\in {\mathbb{\mathbb{N}}}_0$ taka, że jeśli dla każdego słowa $w$ o długości $|w|\le p$ spełniona jest implikacja $w\in L({𝒜})\Rightarrow w\in L({ℬ})$, to

$L({𝒜})\subseteq L({ℬ})$

Rozwiązanie

Niech ${𝒞}$ będzie automatem takim, że $L({𝒞})=L({𝒜})\cup L({ℬ})$. Wówczas,

$L({𝒞})\subseteq L({ℬ})\iff L({𝒜})\subseteq L({ℬ})$.

Udowodnimy więc inkluzję $L({𝒞})\subseteq L({ℬ})$, gdzie

${𝒞}=(S\times Q,f\times g,(s_0,t_0),(S\times F\cup T\times Q))$.

Przyjmijmy $p=|S|\cdot |Q|$. Niech $w\in L({𝒞})$

1. Jeśli $|w|\le p$, to z założenia $w\in L({ℬ})$
2. Jeśli $|w|>p$, to z lematu o pompowaniu wynika, że $\mathrm{\exists }{v}_1{v}_2\in A^{*}$, $\mathrm{\exists }u\in A^{+}$ takie, że $w=v_{1}u{v}_2$, $v_1{v}_2\in L({𝒞})$ i $|v_1{v}_2|<|w|$.

$(f\times g)((s_0,t_0),w)=(f\times g)((s_0,t_0),v_1{v}_2)=(f(s_0,v_1{v}_2),g(t_0,v_1{v}_2))\in S\times F\cup T\times Q$

Mamy dwie możliwości:

(a) $g(t_0,v_1{v}_2)\in F$, co oznacza $v_1{v}_2\in L({ℬ})$, $w\in L({ℬ})$,

(b) $f(s_0,v_1{v}_2)\in T$, co oznacza $v_1{v}_2\in L({𝒜})$.

Jeśli $|v_1{v}_2|<p$, to $v_1{v}_2\in L({ℬ})$, $w\in L({ℬ})$.

Jeśli $|v_1{v}_2|>p$, to powtarzamy punkt 2.

Po każdym kroku długość rozważanego słowa silnie maleje, więc po skończonej ilości kroków uzyskamy oczekiwany efekt.
Zauważ, że z zadania tego wynika rozstrzygalność problemu równoważności automatów. Algorytmiczny aspekt tego problemu rozważymy w ćwiczeniach 8.

Ćwiczenie 4

Niech $A$ będzie dowolnym alfabetem, a $L\subset A^{*}$ językiem regularnym. Udowodnij, że język $L^{\prime }=\{a^{|w|}:w\in L\}$ jest też językiem regularnym.

Rozwiązanie

Rozważmy homomorfizm $h:A^{*}⟶\{a{\}}^{*}$ taki, że $\mathrm{\forall }x\in Af(x)=a$. Dla tak zdefiniowanego $h$ język $L^{\prime }$ jest homomorficzym obrazem języka regularnego $L^{\prime }=h(L)$, a więc jest regularny.

Ćwiczenie 5

Udowodnij, że następujące języki nie są regularne:

1. $L=\{a^n:n\text{nie jest liczbą pierwszą;}\}$,
2. $L=\{a^n{b}^m:0\le n,m;n\ne m\}$.

Rozwiązanie punktu 1

Skorzystamy z faktu, że język $L^{\prime }=\{a^n:n\text{ jest liczbą pierwszą;}\}$ nie jest akceptowany ( ćwiczenie 8), a więc nie jest regularny.

$a^{*}=L\cup L^{\prime },L\cap L^{\prime }=\mathrm{\varnothing },\text{a więc}{L}^{\prime }=\bar{L}$

Ponieważ klasa języków regularnych jest zamknięta ze względu na uzupełnienie, to $L\notin {ℛ}{ℰ}{𝒢}$.

Rozwiązanie punktu 2

Język $L^{\prime }=\{a^n{b}^n:0\le n\}$ nie jest akceptowany (patrz 3.1. z wykładu 6), a więc nie jest regularny.

$a^{*}{b}^{*}=L\cup L^{\prime },L\cap L^{\prime }=\mathrm{\varnothing },\text{a więc}{L}^{\prime }=a^{*}{b}^{*}\cap \bar{L}$.

Ponieważ klasa języków regularnych jest zamknięta ze względu na uzupełnienie i przecięcie, to $L\notin {ℛ}{ℰ}{𝒢}$.

ZADANIA DOMOWE

Ćwiczenie 6

Niech $A=\{a,b\}$. Skonstruuj automat ${𝒜}$, taki że

1. $L({𝒜})=L({ℬ})\cup L({𝒞})$, gdzie ${ℬ}=(S_{{ℬ}},A,f_{{ℬ}},s_{{ℬ}},F_{{ℬ}}),{𝒞}=(S_{{𝒞}},A,f_{{𝒞}},s_{{𝒞}},F_{{𝒞}})$, $S_{{ℬ}}=\{s_{{ℬ}},s_1,s_2\},F_{{ℬ}}=\{s_2\},S_{{𝒞}}=\{s_{{𝒞}},{s^{\prime }}_1,{s^{\prime }}_2\},F_{{𝒞}}=\{{s^{\prime }}_2\}$,

$\begin{array}{cccc}{f}_{{ℬ}}& s_{{ℬ}}& s_1& s_2\\ a& s_2& s_1& s_2\\ b& s_1& s_1& s_2\end{array}\begin{array}{cccc}{f}_{{𝒞}}& s_{{𝒞}}& {s^{\prime }}_1& {s^{\prime }}_2\\ a& {s^{\prime }}_1& {s^{\prime }}_1& {s^{\prime }}_2\\ b& {s^{\prime }}_2& {s^{\prime }}_1& {s^{\prime }}_2\end{array}$ 2. $L({𝒜})=L({ℬ}{)}^{*}$, gdzie ${ℬ}=(S_{{ℬ}},A,f_{{ℬ}},s_{{ℬ}},F_{{ℬ}})$, $S_{{ℬ}}=\{s_{{ℬ}},s_1,s_2,s_3\},F_{{ℬ}}=\{s_2\}$,

$\begin{array}{ccccc}{f}_{{ℬ}}& s_{{ℬ}}& s_1& s_2& s_3\\ a& s_1& s_3& s_3& s_3\\ b& s_3& s_2& s_3& s_3\end{array}$

Podaj dwie konstrukcje:

1. opartą na dowodzie twierdzenia Kleene'ego,
2. z wykorzystaniem automatu z pustymi przejściami.

Ćwiczenie 7

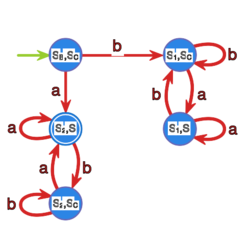
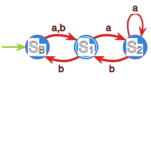
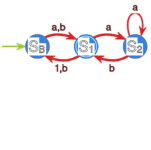
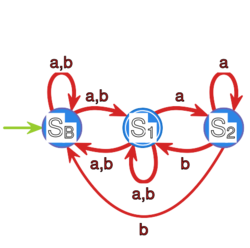
Skonstruuj minimalny automat ${𝒜}$, taki że $L({𝒜})=L({ℬ}{)}^{*}$, gdzie ${ℬ}$ opisany jest

poniższym grafem: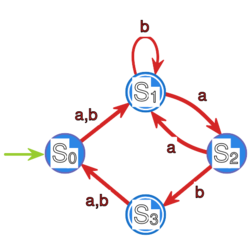

Rysunek 5

Ćwiczenie 8

Udowodnij, że następujące języki nie są regularne:

1. $L=\{a^n{b}^m{c}^n:0<n,m\}$,
2. $L=\{(ab{)}^n(bc{)}^n:n\ge 0\}$.
   

Wskazówka do punktu 2

Wykorzystaj fakt, że język $\{a^n{b}^n:n\ge 0\}$ nie jest regularny oraz domkniętość klasy języków regularnych ze względu na homomorfizm.

Ćwiczenie 9

Zbuduj automat akceptujący język będący ogółem skończonych sekwencji binarnych, w których liczba zer jest podzielna przez dwa, a liczba jedynek przez 3, a następnie gramatykę generującą ten język.

Wskazówka

Stany automatu niech będą postaci $(x,y)$, gdzie $x\in \{0,1\}$, $y\in \{0,1,2\}$. Stan początkowy to $(0,0)$. Określ funkcję przejść w ten sposób, że po przeczytaniu przez automat słowa zawierającego $k$ symboli 0 oraz $l$ symboli 1 automat znajdzie się w stanie $(kmod2,lmod3)$. Zastanów się, który stan będzie stanem końcowym. Na podstawie automatu określ gramatykę.