Pr-1st-1.1-m07-Slajd27: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
m Zastępowanie tekstu – „ </math>” na „</math>” |
m Zastępowanie tekstu – „<math> ” na „<math>” |
||
| Linia 9: | Linia 9: | ||
<math> \mathit\Sigma (\tau )= | <math>\mathit\Sigma (\tau )= | ||
\left \langle S_1(\tau), S_2(\tau), S_3(\tau), L_{1,2}(\tau), L_{2,3}(\tau),L_{3,1}(\tau) \right \rangle</math> | \left \langle S_1(\tau), S_2(\tau), S_3(\tau), L_{1,2}(\tau), L_{2,3}(\tau),L_{3,1}(\tau) \right \rangle</math> | ||
Aktualna wersja na dzień 22:12, 11 wrz 2023
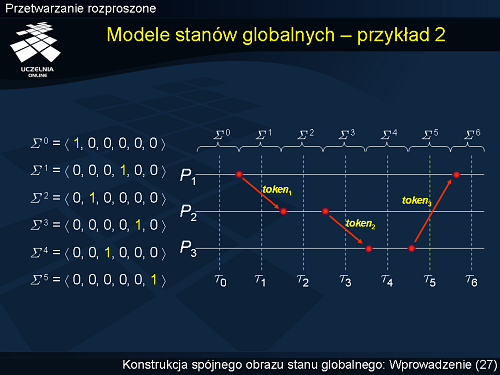
Modele stanów globalnych – przykład 2
Niech dla prostoty zapisu „1” oznacza obecność znacznika, a „0” – jego brak.
W efekcie stan globalny możemy przedstawić w naszym przypadku wsposób następujący:
Tym samym kolejne stany mają postać:
- - znacznik jest w posiadaniu procesu , kanały są puste.
- - znacznik znajduje się w kanale (został wysłany przez ale jeszcze nie został odebrany przez )
- - znacznik jest w posiadaniu procesu , kanały są puste.
- - znacznik znajduje się w kanale (został wysłany przez ale jeszcze nie został odebrany przez )
- - znacznik jest w posiadaniu procesu , kanały są puste.
- - znacznik znajduje się w kanale
(został wysłany przez ale jeszcze nie został odebrany przez )