PKow: Różnice pomiędzy wersjami
m Zastępowanie tekstu – „<math> ” na „<math>” |
m Zastępowanie tekstu – „,↵</math>” na „</math>,” |
||
| (Nie pokazano 1 pośredniej wersji utworzonej przez tego samego użytkownika) | |||
| Linia 25: | Linia 25: | ||
przybliżeń <math>x_k</math> według wzoru | przybliżeń <math>x_k</math> według wzoru | ||
<center><math>x_k\,=\,\phi( x_{k-1}),\qquad k\ge 1 | <center><math>x_k\,=\,\phi( x_{k-1}),\qquad k\ge 1</math></center> | ||
</math></center> | |||
{{twierdzenie|Banacha, o zbieżności iteracji prostej|| | {{twierdzenie|Banacha, o zbieżności iteracji prostej|| | ||
| Linia 87: | Linia 86: | ||
<center><math>\phi(\vec\alpha)\,=\,\phi\Big(\lim_{k\to\infty} x_k\Big) | <center><math>\phi(\vec\alpha)\,=\,\phi\Big(\lim_{k\to\infty} x_k\Big) | ||
\,=\,\lim_{k\to\infty}\phi( x_k) | \,=\,\lim_{k\to\infty}\phi( x_k) | ||
\,=\,\lim_{k\to\infty} x_k\,=\,\vec\alpha | \,=\,\lim_{k\to\infty} x_k\,=\,\vec\alpha</math>,</center> | ||
</math></center> | |||
tzn. <math>\vec\alpha</math> jest punktem stałym odwzorowania <math>\phi</math>. | tzn. <math>\vec\alpha</math> jest punktem stałym odwzorowania <math>\phi</math>. | ||
| Linia 111: | Linia 109: | ||
najmniej liniowo z ilorazem <math>L</math>, tzn. | najmniej liniowo z ilorazem <math>L</math>, tzn. | ||
<center><math>\| x_k- x^*\|\,\le\,L^k\,\| x_0- x^*\| | <center><math>\| x_k- x^*\|\,\le\,L^k\,\| x_0- x^*\|</math></center> | ||
</math></center> | |||
}} | }} | ||
| Linia 128: | Linia 125: | ||
stałą | stałą | ||
<center><math>L\,=\,\max_{0\le x\le 1}|\cos'(x)|\,=\,\sin(1)\,<\,1 | <center><math>L\,=\,\max_{0\le x\le 1}|\cos'(x)|\,=\,\sin(1)\,<\,1</math></center> | ||
</math></center> | |||
Stąd istnieje dokładnie jedno rozwiązanie naszego równania | Stąd istnieje dokładnie jedno rozwiązanie naszego równania | ||
| Linia 196: | Linia 192: | ||
Jeśli <math>x = k + t</math>, gdzie <math>t \in [0,1)</math>, a <math>k</math> jest całkowite, to oczywiście | Jeśli <math>x = k + t</math>, gdzie <math>t \in [0,1)</math>, a <math>k</math> jest całkowite, to oczywiście | ||
<center><math> | <center><math> | ||
e^x = e^{k+t} = e^k e^t = e^k \exp(t) | e^x = e^{k+t} = e^k e^t = e^k \exp(t)</math></center> | ||
</math></center> | |||
Tak więc zadanie redukuje się do wyznaczenia <math>\exp(t)</math> dla ''małego'' <math>t</math> oraz | Tak więc zadanie redukuje się do wyznaczenia <math>\exp(t)</math> dla ''małego'' <math>t</math> oraz | ||
Aktualna wersja na dzień 21:48, 11 wrz 2023
Flash
<flash>file=Test19.swf|width=750|height=530</flash> http://osilek.mimuw.edu.pl/images/2/29/Test19.swf
Metoda iteracji prostej Banacha
 Zupełnie inne, i jak się okaże --- przy odrobinie sprytu bardzo skuteczne --- podejście do wyznaczania miejsca zerowego jest oparte na metodzie Banacha.
Najpierw nasze równanie nieliniowe
przekształcamy (dobierając odpowiednią funkcję ) do równania równoważnego (tzn. mającego te same rozwiązania)
Następnie, startując z pewnego przybliżenia początkowego , konstruujemy ciąg kolejnych przybliżeń według wzoru
Twierdzenie Banacha, o zbieżności iteracji prostej
Niech będzie domkniętym podzbiorem dziedziny ,
w którym jest odwzorowaniem zwężającym. To znaczy, , oraz istnieje stała taka, że
Wtedy równanie
ma dokładnie jedno rozwiązanie , oraz
dla dowolnego przybliżenia początkowego .
Dowód
Wobec
dla mamy
Ciąg jest więc ciągiem Cauchy'ego. Stąd istnieje granica , która należy do , wobec domkniętości tego zbioru. Ponieważ lipschitzowskość implikuje jej ciągłość, mamy też
tzn. jest punktem stałym odwzorowania . Dla jednoznaczności zauważmy, że jeśliby istniał drugi, różny od , punkt stały , to mielibyśmy
Stąd , co jest sprzeczne z założeniem, że
jest zwężająca.Z powyższych rozważań otrzymujemy natychmiastowy wniosek dotyczący zbieżności iteracji prostych.
Wniosek
Przy założeniach Uzupe�nij: twierdzenia Banacha, metoda iteracji prostych jest zbieżna co najmniej liniowo z ilorazem , tzn.
Przykład
Dla ilustracji, rozpatrzmy natępujące proste równanie skalarne:
W tym przypadku . Zauważamy, że w przedziale funkcja jest zwężająca ze stałą
Stąd istnieje dokładnie jedno rozwiązanie naszego równania w przedziale . Rozwiązanie to może być aproksymowane z dowolnie małym błędem przy pomocy iteracji prostych, startując z dowolnego przybliżenia początkowego .
Zaletą iteracji prostych jest fakt, że zbieżność nie zależy od wymiaru zadania, ale tylko od stałej Lipschitza (jednak w praktyce czasem sama stała Lipschitza może zależeć od wymiaru zadania...). Metoda Banacha ma szczególne zastosowanie w przypadku, gdy funkcja jest zwężająca na całym zbiorze , tzn. . Jeśli ponadto ma skończoną średnicę , to dla osiągnięcia -aproksymacji zera funkcji wystarczy wykonać
iteracji, niezależnie od . Metody zbieżne dla dowolnego przybliżenia początkowego, nazywamy zbieżnymi globalnie. Obie przedstawione dotychczas metody: bisekcji i Banacha, przy rozsądnych założeniach, są zbieżne globalnie.
Okazuje się, że metoda iteracji prostej może być --- w bardzo szczególnych przypadkach --- zbieżna szybciej niż liniowo. Z taką sytuacją będziemy mieli, gdy korzystać będziemy z metody Newtona.
Wyznaczanie wektorów i wartości własnych
Przykład Moj przykład
Algorytm Nie robiący nic
Leż
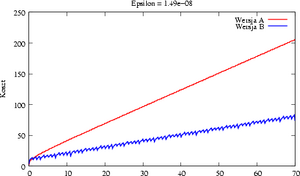



Ćwiczenie: Ciag dalszy
Spróbuj obniżyć koszt wyznaczania dla dużych !