CWGI Moduł 3: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
m Zastępowanie tekstu – „<math> ” na „<math>” |
m Zastępowanie tekstu – „\</math>” na „\ </math>” |
||
| Linia 27: | Linia 27: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:CWGI_M3_Slajd4.png]] | |valign="top" width="500px"|[[Grafika:CWGI_M3_Slajd4.png]] | ||
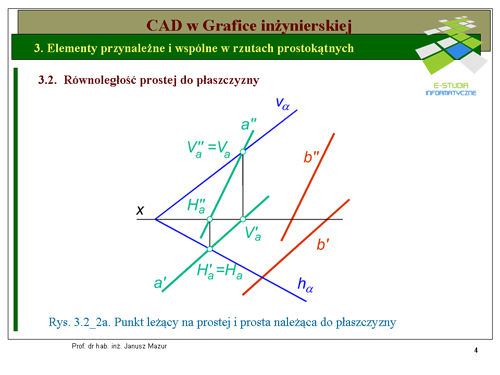
|valign="top"|Bardziej złożona jest konstrukcja równoległości prostej do płaszczyzny w przypadku, gdy płaszczyzna określona jest śladami (rys. 3.2_2a). Wynika to z konieczności wyznaczenia w pierwszej kolejności prostej <math>a\</math>, leżącej w płaszczyźnie. Przypomnijmy tu warunek przynależności prostej do płaszczyzny (ślady prostej muszą leżeć na śladach płaszczyzny). Po wyznaczeniu rzutów prostej '''a''' leżącej w płaszczyźnie <math>\alpha\</math>,bez trudu można wyznaczyć rzuty prostej <math>b || \alpha</math> Rzut pionowy prostej <math>b''</math> będzie równoległy do rzutu pionowego prostej <math>a''</math>, natomiast rzut poziomy prostej <math>b'\</math>, będzie równoległy do rzutu poziomego prostej <math>a''</math> jeżącej w płaszczyźnie <math>\alpha\</math>,. | |valign="top"|Bardziej złożona jest konstrukcja równoległości prostej do płaszczyzny w przypadku, gdy płaszczyzna określona jest śladami (rys. 3.2_2a). Wynika to z konieczności wyznaczenia w pierwszej kolejności prostej <math>a\ </math>, leżącej w płaszczyźnie. Przypomnijmy tu warunek przynależności prostej do płaszczyzny (ślady prostej muszą leżeć na śladach płaszczyzny). Po wyznaczeniu rzutów prostej '''a''' leżącej w płaszczyźnie <math>\alpha\ </math>,bez trudu można wyznaczyć rzuty prostej <math>b || \alpha</math> Rzut pionowy prostej <math>b''</math> będzie równoległy do rzutu pionowego prostej <math>a''</math>, natomiast rzut poziomy prostej <math>b'\ </math>, będzie równoległy do rzutu poziomego prostej <math>a''</math> jeżącej w płaszczyźnie <math>\alpha\ </math>,. | ||
|} | |} | ||
| Linia 36: | Linia 36: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:CWGI_M3_Slajd5.png]] | |valign="top" width="500px"|[[Grafika:CWGI_M3_Slajd5.png]] | ||
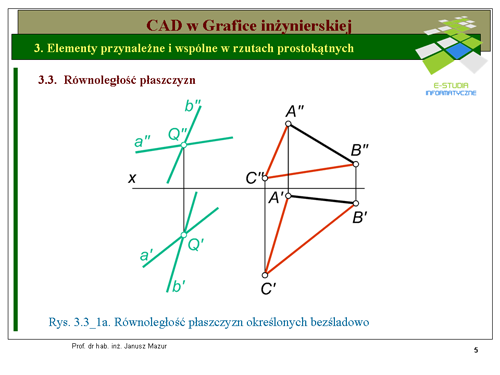
|valign="top"|Równoległość płaszczyzn w rzutach prostokątnych można zdefiniować w sposób następujący:, jeżeli dwie przecinające się proste są równoległe do dwóch innych, przecinających się prostych, to płaszczyzny, jakie tworzą te proste są do siebie równoległe. Można to przedstawić na rys. 3.3_1a. Jedna z płaszczyzn jest określona przez dwie proste przecinające się, druga również, lecz w postaci trójkąta. Płaszczyzna określona przy pomocy dwóch prostych <math>(a x b)</math> przecinających się w punkcie <math>Q\</math>, jest równoległa do płaszczyzny <math>\Delta (ABC)</math>, ponieważ rzuty prostych <math>a\ i\ b</math> są | |valign="top"|Równoległość płaszczyzn w rzutach prostokątnych można zdefiniować w sposób następujący:, jeżeli dwie przecinające się proste są równoległe do dwóch innych, przecinających się prostych, to płaszczyzny, jakie tworzą te proste są do siebie równoległe. Można to przedstawić na rys. 3.3_1a. Jedna z płaszczyzn jest określona przez dwie proste przecinające się, druga również, lecz w postaci trójkąta. Płaszczyzna określona przy pomocy dwóch prostych <math>(a x b)</math> przecinających się w punkcie <math>Q\ </math>, jest równoległa do płaszczyzny <math>\Delta (ABC)</math>, ponieważ rzuty prostych <math>a\ i\ b</math> są | ||
odpowiednio równoległe do rzutów boków <math>AC\ i CB\ \Delta (ABC)</math>. | odpowiednio równoległe do rzutów boków <math>AC\ i CB\ \Delta (ABC)</math>. | ||
| Linia 74: | Linia 74: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:CWGI_M3_Slajd9.png]] | |valign="top" width="500px"|[[Grafika:CWGI_M3_Slajd9.png]] | ||
|valign="top"|Prosta jest prostopadła do płaszczyzny, jeżeli jest prostopadła do dwóch przecinających się prostych leżących w tej płaszczyźnie. Prostopadłość prostej do płaszczyzny ustalana jest w rzutach prostokątnych poprzez konstrukcję prostopadłości dwu prostych. Rzuty prostej prostopadłej do danej płaszczyzny powinny być, zatem prostopadłe odpowiednio do rzutu poziomego prostej poziomej leżącej w płaszczyźnie oraz do rzutu pionowego prostej czołowej leżącej w płaszczyźnie. Aby zatem poprowadzić prostą prostopadłą do płaszczyzny określonej bezśladowo należy wyznaczyć dwie przecinające się proste (poziomą i czołową) leżące w tej płaszczyźnie. Umożliwi to nam wyznaczenie prostej, która będzie prostopadła do jednej i drugiej prostej. Oczywiście, w sensie ogólnym, prosta jest prostopadła do płaszczyzny, jeżeli jest prostopadła do dowolnych przecinających się prostych leżących w płaszczyźnie, jednak konstrukcję taką można zrealizować w rzutowaniu prostokątnym tylko wtedy, jeżeli oprzemy się na prostych szczególnych, ponieważ ich pojedyncze ramiona są równoległe do rzutni. Zamiast wyznaczać proste szczególne leżące w płaszczyźnie, możemy samą płaszczyznę przedstawić przy pomocy dwóch przecinających się prostych - poziomej i czołowej. Na rys. 3.5_1a przedstawiono konstrukcję płaszczyzny <math\alpha(p x c)</math> określonej przy pomocy dwóch prostych: poziomej i czołowej przecinających się w punkcie <math>1\</math>,. Prosta <math>n\</math>, jest prostopadła do płaszczyzny <math>\alpha</math>ponieważ jej rzuty są odpowiednio prostopadłe do rzutu pionowego prostej czołowej i rzutu poziomego prostej czołowej. | |valign="top"|Prosta jest prostopadła do płaszczyzny, jeżeli jest prostopadła do dwóch przecinających się prostych leżących w tej płaszczyźnie. Prostopadłość prostej do płaszczyzny ustalana jest w rzutach prostokątnych poprzez konstrukcję prostopadłości dwu prostych. Rzuty prostej prostopadłej do danej płaszczyzny powinny być, zatem prostopadłe odpowiednio do rzutu poziomego prostej poziomej leżącej w płaszczyźnie oraz do rzutu pionowego prostej czołowej leżącej w płaszczyźnie. Aby zatem poprowadzić prostą prostopadłą do płaszczyzny określonej bezśladowo należy wyznaczyć dwie przecinające się proste (poziomą i czołową) leżące w tej płaszczyźnie. Umożliwi to nam wyznaczenie prostej, która będzie prostopadła do jednej i drugiej prostej. Oczywiście, w sensie ogólnym, prosta jest prostopadła do płaszczyzny, jeżeli jest prostopadła do dowolnych przecinających się prostych leżących w płaszczyźnie, jednak konstrukcję taką można zrealizować w rzutowaniu prostokątnym tylko wtedy, jeżeli oprzemy się na prostych szczególnych, ponieważ ich pojedyncze ramiona są równoległe do rzutni. Zamiast wyznaczać proste szczególne leżące w płaszczyźnie, możemy samą płaszczyznę przedstawić przy pomocy dwóch przecinających się prostych - poziomej i czołowej. Na rys. 3.5_1a przedstawiono konstrukcję płaszczyzny <math\alpha(p x c)</math> określonej przy pomocy dwóch prostych: poziomej i czołowej przecinających się w punkcie <math>1\ </math>,. Prosta <math>n\ </math>, jest prostopadła do płaszczyzny <math>\alpha</math>ponieważ jej rzuty są odpowiednio prostopadłe do rzutu pionowego prostej czołowej i rzutu poziomego prostej czołowej. | ||
W przypadku płaszczyzny określonej śladami konstrukcja prostej prostopadłej do płaszczyzny jest znacznie łatwiejsza, ponieważ rzuty prostej powinny być prostopadłe do odpowiednich śladów płaszczyzny (rys. 3.5_1b). Nie kłóci się to z poprzednimi ustaleniami, albowiem ślady płaszczyzny są szczególnie położonymi prostymi: poziomą i czołową, które leżą w płaszczyźnie i jednocześnie leżą na rzutniach. Ślady te oczywiście są prostymi, które przecinają się na osi <math>x\</math>,, spełniają, więc wszystkie warunki do realizacji konstrukcji prostopadłości prostej do płaszczyzny. | W przypadku płaszczyzny określonej śladami konstrukcja prostej prostopadłej do płaszczyzny jest znacznie łatwiejsza, ponieważ rzuty prostej powinny być prostopadłe do odpowiednich śladów płaszczyzny (rys. 3.5_1b). Nie kłóci się to z poprzednimi ustaleniami, albowiem ślady płaszczyzny są szczególnie położonymi prostymi: poziomą i czołową, które leżą w płaszczyźnie i jednocześnie leżą na rzutniach. Ślady te oczywiście są prostymi, które przecinają się na osi <math>x\ </math>,, spełniają, więc wszystkie warunki do realizacji konstrukcji prostopadłości prostej do płaszczyzny. | ||
Na rys. 3.5_1b przedstawiono konstrukcję prostej n prostopadłej do płaszczyzny określonej śladami. Prosta prostopadła do płaszczyzny przechodzi przez z góry określony punkt <math>Q\</math>, w przestrzeni. Jak widać rzut pionowy prostej prostopadłej do płaszczyzny <math>''</math> jest prostopadły do śladu pionowego płaszczyzny <math>v_\alpha</math> (ślad pionowy płaszczyzny jest rzutem prostej czołowej leżącej w płaszczyźnie i leżącej na rzutni pionowej), natomiast rzut poziomy prostej prostopadłej <math>n'</math> jest prostopadły do śladu poziomego <math>h_\alpha</math> (ślad poziomy płaszczyzny jest rzutem prostej poziomej leżącej w płaszczyźnie i leżącej na rzutni poziomej). | Na rys. 3.5_1b przedstawiono konstrukcję prostej n prostopadłej do płaszczyzny określonej śladami. Prosta prostopadła do płaszczyzny przechodzi przez z góry określony punkt <math>Q\ </math>, w przestrzeni. Jak widać rzut pionowy prostej prostopadłej do płaszczyzny <math>''</math> jest prostopadły do śladu pionowego płaszczyzny <math>v_\alpha</math> (ślad pionowy płaszczyzny jest rzutem prostej czołowej leżącej w płaszczyźnie i leżącej na rzutni pionowej), natomiast rzut poziomy prostej prostopadłej <math>n'</math> jest prostopadły do śladu poziomego <math>h_\alpha</math> (ślad poziomy płaszczyzny jest rzutem prostej poziomej leżącej w płaszczyźnie i leżącej na rzutni poziomej). | ||
| Linia 89: | Linia 89: | ||
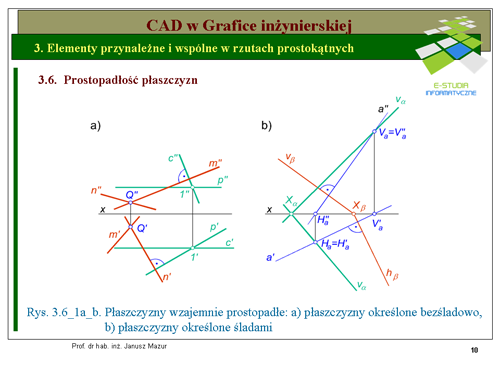
|valign="top"|Dwie płaszczyzny są do siebie prostopadłe, jeżeli jedna z nich zawiera prostą prostopadłą do drugiej płaszczyzny. Można, zatem stwierdzić, że każda płaszczyzna przechodząca przez prostą prostopadłą do płaszczyzny jest do niej prostopadła. A więc przez prostą prostopadłą do płaszczyzny można poprowadzić cały pęk płaszczyzn, które będą prostopadłe do danej płaszczyzny. Na rys.3.6_1a,b przedstawiono płaszczyzny prostopadłe do z góry zadanych płaszczyzn. | |valign="top"|Dwie płaszczyzny są do siebie prostopadłe, jeżeli jedna z nich zawiera prostą prostopadłą do drugiej płaszczyzny. Można, zatem stwierdzić, że każda płaszczyzna przechodząca przez prostą prostopadłą do płaszczyzny jest do niej prostopadła. A więc przez prostą prostopadłą do płaszczyzny można poprowadzić cały pęk płaszczyzn, które będą prostopadłe do danej płaszczyzny. Na rys.3.6_1a,b przedstawiono płaszczyzny prostopadłe do z góry zadanych płaszczyzn. | ||
Na rys. 3.6_1a dana jest płaszczyzna określona za pomocą dwóch przecinających się w punkcie 1 prostych <math>p\ i\ c</math>. Druga płaszczyzna prostopadła do pierwszej określona została za pomocą również dwóch prostych m i n przecinających się w punkcie <math>Q\</math>,, przy czym jedna z nich jest prostopadła do płaszczyzny utworzonej przez proste <math>p\ i\ c</math>. Wynika to z faktu, iż proste <math>p\ i\ c</math> są odpowiednio równoległe do rzutni poziomej (prosta pozioma p) i rzutni pionowej (prosta czołowa c), a więc prosta <math>n\</math>, będzie prostopadła do płaszczyzny utworzonej przez te proste, jeżeli rzut pionowy prostej <math>n''</math> będzie prostopadły do rzutu pionowego prostej czołowej <math>c''</math>, a rzut poziomy prostej <math>n'</math> będzie prostopadły do rzutu poziomego prostej poziomej <math>p'</math>. | Na rys. 3.6_1a dana jest płaszczyzna określona za pomocą dwóch przecinających się w punkcie 1 prostych <math>p\ i\ c</math>. Druga płaszczyzna prostopadła do pierwszej określona została za pomocą również dwóch prostych m i n przecinających się w punkcie <math>Q\ </math>,, przy czym jedna z nich jest prostopadła do płaszczyzny utworzonej przez proste <math>p\ i\ c</math>. Wynika to z faktu, iż proste <math>p\ i\ c</math> są odpowiednio równoległe do rzutni poziomej (prosta pozioma p) i rzutni pionowej (prosta czołowa c), a więc prosta <math>n\ </math>, będzie prostopadła do płaszczyzny utworzonej przez te proste, jeżeli rzut pionowy prostej <math>n''</math> będzie prostopadły do rzutu pionowego prostej czołowej <math>c''</math>, a rzut poziomy prostej <math>n'</math> będzie prostopadły do rzutu poziomego prostej poziomej <math>p'</math>. | ||
W przypadku konstrukcji śladowych (rys. 3.6_1b) w dowolnej płaszczyźnie <math>\alpha</math>określonej śladami <math>v_\alpha i h_\alpha</math>obieramy dowolną prostą a leżącą w płaszczyźnie, a więc jej ślady <math>V_\alpha i H_\alpha</math> będą leżały na śladach płaszczyzny. W ten sposób skonstruowane rzuty prostej <math>a\</math>, leżącej w płaszczyźnie <math>\alpha\</math>, powinny być prostopadłe do odpowiednich śladów płaszczyzny <math>\beta</math>. Zatem możemy stwierdzić, że płaszczyzna <math>\beta</math> jest prostopadła do <math>\alpha</math>, ponieważ jest prostopadła do prostej <math>a\</math>,, która leży w płaszczyźnie <math>\alpha\</math>,. | W przypadku konstrukcji śladowych (rys. 3.6_1b) w dowolnej płaszczyźnie <math>\alpha</math>określonej śladami <math>v_\alpha i h_\alpha</math>obieramy dowolną prostą a leżącą w płaszczyźnie, a więc jej ślady <math>V_\alpha i H_\alpha</math> będą leżały na śladach płaszczyzny. W ten sposób skonstruowane rzuty prostej <math>a\ </math>, leżącej w płaszczyźnie <math>\alpha\ </math>, powinny być prostopadłe do odpowiednich śladów płaszczyzny <math>\beta</math>. Zatem możemy stwierdzić, że płaszczyzna <math>\beta</math> jest prostopadła do <math>\alpha</math>, ponieważ jest prostopadła do prostej <math>a\ </math>,, która leży w płaszczyźnie <math>\alpha\ </math>,. | ||
| Linia 103: | Linia 103: | ||
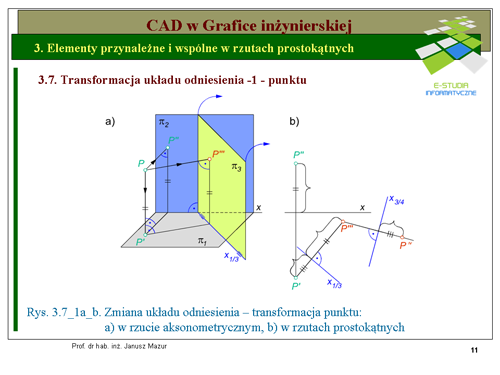
1. obrać w sposób dowolny oś transformacji (ślad, krawędź przecięcia się nowej rzutni <math>\pi_3</math> z rzutnią poziomą). Oś transformacji oznaczać będziemy <math>x_{1/3}</math> , | 1. obrać w sposób dowolny oś transformacji (ślad, krawędź przecięcia się nowej rzutni <math>\pi_3</math> z rzutnią poziomą). Oś transformacji oznaczać będziemy <math>x_{1/3}</math> , | ||
2. trzeci rzut punktu będzie leżał na odnoszącej prostopadłej do osi transformacji, co wynika z obrotu trzeciej rzutni <math>pi_3</math> do położenia na rzutni poziomej <math>pi_1</math> . Odległość, w jakiej będzie się znajdował trzeci rzut punktu <math>P'''</math> od osi <math>x\</math>, jest równa wysokości punktu <math>P\</math>,, czyli odległości tego punktu od rzutni poziomej. Ta odległość jest oczywiście taka sama jak odległość rzutu pionowego punktu <math>P''</math> od osi <math>x\</math>,. Można, zatem stwierdzić, iż odmierzamy od osi <math>x_{1/3}</math> odległość poprzedniego rzutu (<math>P"</math>) punktu od poprzedniej osi (x), | 2. trzeci rzut punktu będzie leżał na odnoszącej prostopadłej do osi transformacji, co wynika z obrotu trzeciej rzutni <math>pi_3</math> do położenia na rzutni poziomej <math>pi_1</math> . Odległość, w jakiej będzie się znajdował trzeci rzut punktu <math>P'''</math> od osi <math>x\ </math>, jest równa wysokości punktu <math>P\ </math>,, czyli odległości tego punktu od rzutni poziomej. Ta odległość jest oczywiście taka sama jak odległość rzutu pionowego punktu <math>P''</math> od osi <math>x\ </math>,. Można, zatem stwierdzić, iż odmierzamy od osi <math>x_{1/3}</math> odległość poprzedniego rzutu (<math>P"</math>) punktu od poprzedniej osi (x), | ||
3. taką operację możemy powtarzać w miarę potrzeby wielokrotnie, zachowując opisane powyżej zasady. Na rys. 3.7_1a,b przedstawiono dwie kolejne transformacje punktu <math>P\</math>, w rzucie aksonometrycznym i prostokątnym. | 3. taką operację możemy powtarzać w miarę potrzeby wielokrotnie, zachowując opisane powyżej zasady. Na rys. 3.7_1a,b przedstawiono dwie kolejne transformacje punktu <math>P\ </math>, w rzucie aksonometrycznym i prostokątnym. | ||
| Linia 115: | Linia 115: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:CWGI_M3_Slajd12.png]] | |valign="top" width="500px"|[[Grafika:CWGI_M3_Slajd12.png]] | ||
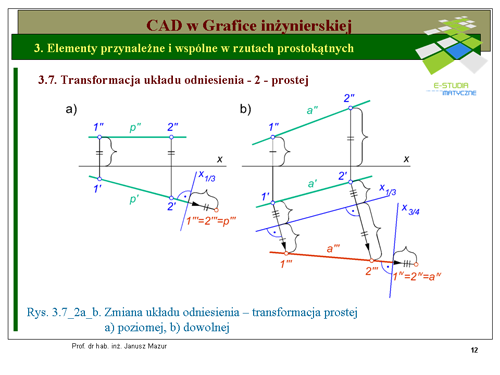
|valign="top"| Transformacja prostej, to nic innego jak transformacja dwóch punktów należących do niej. Transformację prostej wykonujemy w określonym celu. Zwykle dotyczy to sprowadzania prostej do położenia rzutującego, to znaczy do położenia prostopadłego do rzutni. Takie położenie prostej może być wykorzystywane do rozwiązywania szeregu konstrukcji (np. wyznaczania rzeczywistej odległości dwu prostych skośnych). Sprowadzenie prostej do położenia rzutującego za pomocą transformacji uwarunkowane jest położeniem danej prostej. Położenie prostej równoległe do rzutni umożliwia dokonanie takiej operacji za pomocą '''jednej''' transformacji. W tym bowiem przypadku jesteśmy w stanie zaproponować trzecią rzutnię prostopadle do prostej (oś transformacji będzie prostopadła do rzutu poziomego prostej, jeżeli prosta jest równoległa do rzutni poziomej lub prostopadła do rzutu pionowego, jeżeli jest ona równoległa do rzutni pionowej). Na rys.3.7_2a. przedstawiono transformację prostej poziomej (równoległej do rzutni poziomej). Prosta '''p''' jest prostą poziomą, więc sprowadzenie jej do położenia rzutującego (do punktu) jest możliwe za pomocą jednej transformacji o osi <math>x_{1/3}</math> prostopadłej do rzutu poziomego prostej. Dokonując transformacji prostej, należy dokonać transformacji dwóch dowolnych punktów należących do niej. Obieramy dwa punkty <math>1\ i \2</math> leżące na prostej, a następnie dokonujemy transformacji tych punktów o osi <math>x_{1/3}</math> . Odmierzając na odnoszącej przechodzącej przez punkty <math>1'\ i\ 2'</math> i prostopadłej do osi transformacji odległość równą wysokości punktów <math>1\ i\ 2</math> (odległość <math>1" \i\ 2"</math> od osi <math>x\</math>,) wyznaczymy trzecie rzuty punktów <math>1'''\ i\ 2'''</math>, a tym samym i trzeci rzut prostej <math>p'''</math>. | |valign="top"| Transformacja prostej, to nic innego jak transformacja dwóch punktów należących do niej. Transformację prostej wykonujemy w określonym celu. Zwykle dotyczy to sprowadzania prostej do położenia rzutującego, to znaczy do położenia prostopadłego do rzutni. Takie położenie prostej może być wykorzystywane do rozwiązywania szeregu konstrukcji (np. wyznaczania rzeczywistej odległości dwu prostych skośnych). Sprowadzenie prostej do położenia rzutującego za pomocą transformacji uwarunkowane jest położeniem danej prostej. Położenie prostej równoległe do rzutni umożliwia dokonanie takiej operacji za pomocą '''jednej''' transformacji. W tym bowiem przypadku jesteśmy w stanie zaproponować trzecią rzutnię prostopadle do prostej (oś transformacji będzie prostopadła do rzutu poziomego prostej, jeżeli prosta jest równoległa do rzutni poziomej lub prostopadła do rzutu pionowego, jeżeli jest ona równoległa do rzutni pionowej). Na rys.3.7_2a. przedstawiono transformację prostej poziomej (równoległej do rzutni poziomej). Prosta '''p''' jest prostą poziomą, więc sprowadzenie jej do położenia rzutującego (do punktu) jest możliwe za pomocą jednej transformacji o osi <math>x_{1/3}</math> prostopadłej do rzutu poziomego prostej. Dokonując transformacji prostej, należy dokonać transformacji dwóch dowolnych punktów należących do niej. Obieramy dwa punkty <math>1\ i \2</math> leżące na prostej, a następnie dokonujemy transformacji tych punktów o osi <math>x_{1/3}</math> . Odmierzając na odnoszącej przechodzącej przez punkty <math>1'\ i\ 2'</math> i prostopadłej do osi transformacji odległość równą wysokości punktów <math>1\ i\ 2</math> (odległość <math>1" \i\ 2"</math> od osi <math>x\ </math>,) wyznaczymy trzecie rzuty punktów <math>1'''\ i\ 2'''</math>, a tym samym i trzeci rzut prostej <math>p'''</math>. | ||
Sprowadzenie prostej w położeniu dowolnym do położenia rzutującego (do punktu) możliwe jest za pomocą podwójnej transformacji (3.7_2b). W pierwszej sprowadzamy prostą do położenia równoległego z trzecią rzutnią, a następnie za pomocą rzutni czwartej prostopadłej do trzeciego rzutu sprowadzamy ją do położenia rzutującego. W pierwszej transformacji przyjmujemy trzecią rzutnię równolegle do prostej oś transformacji <math>x_{1/3}</math> będzie równoległa do rzutu poziomego prostej <math>a'</math>). Druga transformacja o osi <math>x_{3/4}</math> będzie prostopadła do trzeciego rzutu. Odmierzając od osi <math>x_{3/4}</math> odległość rzutu poziomego a' od pierwszej osi transformacji otrzymamy czwarte rzuty punktów oraz czwarty rzut prostej <math>p^{IV}</math>, który również będzie punktem. | Sprowadzenie prostej w położeniu dowolnym do położenia rzutującego (do punktu) możliwe jest za pomocą podwójnej transformacji (3.7_2b). W pierwszej sprowadzamy prostą do położenia równoległego z trzecią rzutnią, a następnie za pomocą rzutni czwartej prostopadłej do trzeciego rzutu sprowadzamy ją do położenia rzutującego. W pierwszej transformacji przyjmujemy trzecią rzutnię równolegle do prostej oś transformacji <math>x_{1/3}</math> będzie równoległa do rzutu poziomego prostej <math>a'</math>). Druga transformacja o osi <math>x_{3/4}</math> będzie prostopadła do trzeciego rzutu. Odmierzając od osi <math>x_{3/4}</math> odległość rzutu poziomego a' od pierwszej osi transformacji otrzymamy czwarte rzuty punktów oraz czwarty rzut prostej <math>p^{IV}</math>, który również będzie punktem. | ||
| Linia 131: | Linia 131: | ||
Mając do czynienia z płaszczyzną określoną bezśladowo osi transformacji przyjmujemy prostopadle do rzutu poziomego prostej poziomej, w pierwszym przypadku, lub do rzutu pionowego prostej czołowej w drugim przypadku. Zatem wstępną czynnością będzie ustalenie rzutów prostej poziomej (czołowej) leżącej w analizowanej płaszczyźnie. Na rys. 3.7_2a przedstawiono konstrukcję zmiany układu odniesienia za pomocą transformacji dla płaszczyzny określonej dwoma prostymi równoległymi oraz określonej śladami na rys. 3.7_2b | Mając do czynienia z płaszczyzną określoną bezśladowo osi transformacji przyjmujemy prostopadle do rzutu poziomego prostej poziomej, w pierwszym przypadku, lub do rzutu pionowego prostej czołowej w drugim przypadku. Zatem wstępną czynnością będzie ustalenie rzutów prostej poziomej (czołowej) leżącej w analizowanej płaszczyźnie. Na rys. 3.7_2a przedstawiono konstrukcję zmiany układu odniesienia za pomocą transformacji dla płaszczyzny określonej dwoma prostymi równoległymi oraz określonej śladami na rys. 3.7_2b | ||
W przypadku sprowadzania płaszczyzny określonej przez dwie proste równoległe do położenia rzutującego obieramy prostą poziomą leżącą w tej płaszczyźnie. Rzut pionowy prostej poziomej <math>p''\</math>, będzie równoległy do osi <math>x\</math>,. Na rzutach poziomych prostych <math>a'\ i\ b'</math> znajdziemy rzuty punktów <math>1'\ i\ 2'</math> należących do tych prostych i w konsekwencji wyznaczymy rzut poziomy prostej <math>p'\</math>,. Wyznaczając oś transformacji <math>x_{1/3}</math> , ustalimy trzecie rzuty punktów <math>1'''\ i\ 2'''</math> oraz <math>p'''\</math>,. Wystarczy, zatem obrać jeszcze jeden punkt (np.3) nie współliniowy z punktami <math>1\ i\ 2</math>, aby po przeprowadzeniu transformacji tego punktu wyznaczyć jego trzeci rzut, przy tej samej osi transformacji. Rzuty punktów <math>1'''\, 2'''</math> oraz <math>3'''\</math>, wyznaczają nam trzeci rzut płaszczyzny, który będzie prostą. Płaszczyzna <math>\alphaa||b</math> ma w układzie <math><\pi_1,\pi_3></math> położenie rzutujące. | W przypadku sprowadzania płaszczyzny określonej przez dwie proste równoległe do położenia rzutującego obieramy prostą poziomą leżącą w tej płaszczyźnie. Rzut pionowy prostej poziomej <math>p''\ </math>, będzie równoległy do osi <math>x\ </math>,. Na rzutach poziomych prostych <math>a'\ i\ b'</math> znajdziemy rzuty punktów <math>1'\ i\ 2'</math> należących do tych prostych i w konsekwencji wyznaczymy rzut poziomy prostej <math>p'\ </math>,. Wyznaczając oś transformacji <math>x_{1/3}</math> , ustalimy trzecie rzuty punktów <math>1'''\ i\ 2'''</math> oraz <math>p'''\ </math>,. Wystarczy, zatem obrać jeszcze jeden punkt (np.3) nie współliniowy z punktami <math>1\ i\ 2</math>, aby po przeprowadzeniu transformacji tego punktu wyznaczyć jego trzeci rzut, przy tej samej osi transformacji. Rzuty punktów <math>1'''\, 2'''</math> oraz <math>3'''\ </math>, wyznaczają nam trzeci rzut płaszczyzny, który będzie prostą. Płaszczyzna <math>\alphaa||b</math> ma w układzie <math><\pi_1,\pi_3></math> położenie rzutujące. | ||
Przy sprowadzaniu płaszczyzny określonej śladami do położenia rzutującego postępujemy bardzo podobnie. W tym przypadku oś transformacji <math>x_{1/3}</math> będzie prostopadła do śladu poziomego płaszczyzny <math>\alpha</math> Ponieważ ślad poziomy płaszczyzny jest szczególnym położeniem prostej poziomej leżącej w płaszczyźnie, to punkt przecięcia się śladu poziomego z osią transformacji <math>x_{1/3}</math> - oznaczony <math>X\alpha''</math>'zwany węzłem płaszczyzny będzie punktem należącym do trzeciego rzutu płaszczyzny. Należy zatem obrać jeszcze jeden punkt nie należący do śladu poziomego (np. punkt 1), aby po dokonaniu transformacji tego punktu, przy tej samej osi <math>x_{1/3}</math> , ustalić jego trzeci rzut. Punkty <math>1'''\ i\ X+\alpha'''</math> wyznaczą nam trzeci rzut płaszczyzny <math>\alpha'''</math>. | Przy sprowadzaniu płaszczyzny określonej śladami do położenia rzutującego postępujemy bardzo podobnie. W tym przypadku oś transformacji <math>x_{1/3}</math> będzie prostopadła do śladu poziomego płaszczyzny <math>\alpha</math> Ponieważ ślad poziomy płaszczyzny jest szczególnym położeniem prostej poziomej leżącej w płaszczyźnie, to punkt przecięcia się śladu poziomego z osią transformacji <math>x_{1/3}</math> - oznaczony <math>X\alpha''</math>'zwany węzłem płaszczyzny będzie punktem należącym do trzeciego rzutu płaszczyzny. Należy zatem obrać jeszcze jeden punkt nie należący do śladu poziomego (np. punkt 1), aby po dokonaniu transformacji tego punktu, przy tej samej osi <math>x_{1/3}</math> , ustalić jego trzeci rzut. Punkty <math>1'''\ i\ X+\alpha'''</math> wyznaczą nam trzeci rzut płaszczyzny <math>\alpha'''</math>. | ||
| Linia 145: | Linia 145: | ||
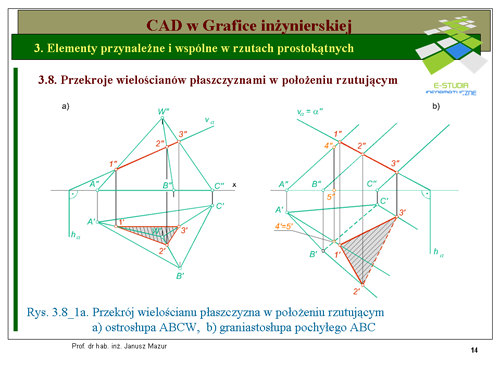
Rozwiążmy zadanie na przykładzie dwóch wielościanów ostrosłupa prostego stojacego na rzutni poziomej i graniastosłupa pochyłego stojacego na rzutni poziomej. W pierwszym przypadku wyznaczymy rzuty przekroju ostrosłupa '''ABCW''' stojącego na rzutni poziomej płaszczyzną pionowo - rzutującą <math>\alpha</math> (rys. 3.8_1a). | Rozwiążmy zadanie na przykładzie dwóch wielościanów ostrosłupa prostego stojacego na rzutni poziomej i graniastosłupa pochyłego stojacego na rzutni poziomej. W pierwszym przypadku wyznaczymy rzuty przekroju ostrosłupa '''ABCW''' stojącego na rzutni poziomej płaszczyzną pionowo - rzutującą <math>\alpha</math> (rys. 3.8_1a). | ||
Zbudujmy w rzutach prostokątnych ostrosłup prosty o podstawie trójkąta stojący na rzutni poziomej oraz przyjmijmy płaszczyznę pionowo - rzutującą określoną śladami <math>v_\alpha\ i\ h_\alpha</math>. Ponieważ płaszczyzna <math>\alpha\</math>, jest rzutująca to wszystkie elementy płaskie znajdujące się w płaszczyźnie, w rzucie pionowym będą znajdować się na rzucie pionowym płaszczyzny <math>\alpha\</math>,, czyli na śladzie pionowym płaszczyzny <math>v_\alpha</math>. Tak więc przekrój w rzucie pionowym wyznaczymy znajdując punkty przecięcia się śladu <math>v_\alpha</math> z rzutami pionowym krawędzi ostrosłupa <math>A''W''</math>, <math>B''W''</math> i<math>C''W''</math>. Przekrój w rzucie pionowym będzie wyznaczony przez rzuty punktów <math>1'',\ 2''\ i\ 3''</math>. Rzut poziomy przekroju wyznaczymy jako wielokąt, którego wierzchołkami są punktami przecięcia odnoszących z rzutami poziomymi krawędzi <math>A'W',\ B'W'\ i\ C'W'</math>. | Zbudujmy w rzutach prostokątnych ostrosłup prosty o podstawie trójkąta stojący na rzutni poziomej oraz przyjmijmy płaszczyznę pionowo - rzutującą określoną śladami <math>v_\alpha\ i\ h_\alpha</math>. Ponieważ płaszczyzna <math>\alpha\ </math>, jest rzutująca to wszystkie elementy płaskie znajdujące się w płaszczyźnie, w rzucie pionowym będą znajdować się na rzucie pionowym płaszczyzny <math>\alpha\ </math>,, czyli na śladzie pionowym płaszczyzny <math>v_\alpha</math>. Tak więc przekrój w rzucie pionowym wyznaczymy znajdując punkty przecięcia się śladu <math>v_\alpha</math> z rzutami pionowym krawędzi ostrosłupa <math>A''W''</math>, <math>B''W''</math> i<math>C''W''</math>. Przekrój w rzucie pionowym będzie wyznaczony przez rzuty punktów <math>1'',\ 2''\ i\ 3''</math>. Rzut poziomy przekroju wyznaczymy jako wielokąt, którego wierzchołkami są punktami przecięcia odnoszących z rzutami poziomymi krawędzi <math>A'W',\ B'W'\ i\ C'W'</math>. | ||
Drugi przykład dotyczy graniastosłupa. Należy wyznaczyć rzuty przekroju graniastosłupa pochyłego '''ABC''' o podstawie na rzutni poziomej płaszczyzną pionowo - rzutującą <math>\alpha\</math>, rys.3.8_1b). | Drugi przykład dotyczy graniastosłupa. Należy wyznaczyć rzuty przekroju graniastosłupa pochyłego '''ABC''' o podstawie na rzutni poziomej płaszczyzną pionowo - rzutującą <math>\alpha\ </math>, rys.3.8_1b). | ||
Przy rozwiązywaniu tego przykładu postępujemy analogicznie jak na rys. 3.8_1a. | Przy rozwiązywaniu tego przykładu postępujemy analogicznie jak na rys. 3.8_1a. | ||
Aktualna wersja na dzień 12:04, 5 wrz 2023

|
Elementy równoległe i prostopadłe |