CWGI Moduł 1: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
m Zastępowanie tekstu – „ \</math>” na „</math>” |
m Zastępowanie tekstu – „\</math>” na „\ </math>” |
||
| (Nie pokazano 1 pośredniej wersji utworzonej przez tego samego użytkownika) | |||
| Linia 13: | Linia 13: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:CWGI_M1_Slajd2.png]] | |valign="top" width="500px"|[[Grafika:CWGI_M1_Slajd2.png]] | ||
|valign="top"|Grafika inżynierska opiera się na prawach i ustaleniach nauki zwanej geometrią. Historycznie, geometria była zbiorem przepisów praktycznych, które dotyczyły wykonywania pomiarów fizycznych przedmiotów materialnych. W starożytności ok. 300 lat przed naszą erą ustalono dla niej znaczące miejsce w opracowaniach greckiego matematyka – Euklidesa. W dziele o nazwie Elementy autor nadał geometrii postać nauki abstrakcyjnej, gdzie przedmiot materialny zastąpiono pojęciem '''figury geometrycznej''', będącej jego emanacją. Własności takiej figury dotyczyły głównie wielkości i kształtu przedmiotu, a więc opierały się na ustaleniu wzajemnych odległości należących do danego przedmiotu. Wprowadzono naukę o tzw. własnościach metrycznych, która charakteryzuje daną figurę oraz wszystkie figury do niej przystające. Przez figury definiowano zbiory punktów należących do pewnego stałego zbioru punktów zwanego przestrzenią, którą przypadku określenia odległości między punktami zbioru nazwano przestrzenią metryczną. Do najbardziej znanych przestrzeni metrycznych należą prosta euklidesowa <math>E_1\</math>,, płaszczyzna euklidesowa <math>E_2\</math>, oraz przestrzeń trójwymiarowa <math>E_3\</math>,. Geometria euklidesowa zbudowana w oparciu o cztery podstawowe grupy aksjomatów | |valign="top"|Grafika inżynierska opiera się na prawach i ustaleniach nauki zwanej geometrią. Historycznie, geometria była zbiorem przepisów praktycznych, które dotyczyły wykonywania pomiarów fizycznych przedmiotów materialnych. W starożytności ok. 300 lat przed naszą erą ustalono dla niej znaczące miejsce w opracowaniach greckiego matematyka – Euklidesa. W dziele o nazwie Elementy autor nadał geometrii postać nauki abstrakcyjnej, gdzie przedmiot materialny zastąpiono pojęciem '''figury geometrycznej''', będącej jego emanacją. Własności takiej figury dotyczyły głównie wielkości i kształtu przedmiotu, a więc opierały się na ustaleniu wzajemnych odległości należących do danego przedmiotu. Wprowadzono naukę o tzw. własnościach metrycznych, która charakteryzuje daną figurę oraz wszystkie figury do niej przystające. Przez figury definiowano zbiory punktów należących do pewnego stałego zbioru punktów zwanego przestrzenią, którą przypadku określenia odległości między punktami zbioru nazwano przestrzenią metryczną. Do najbardziej znanych przestrzeni metrycznych należą prosta euklidesowa <math>E_1\ </math>,, płaszczyzna euklidesowa <math>E_2\ </math>, oraz przestrzeń trójwymiarowa <math>E_3\ </math>,. Geometria euklidesowa zbudowana w oparciu o cztery podstawowe grupy aksjomatów | ||
(o przynależności, o uporządkowaniu, o porównaniu i ciągłości), uzupełnione o aksjomat zwany pewnikiem Euklidesa. | (o przynależności, o uporządkowaniu, o porównaniu i ciągłości), uzupełnione o aksjomat zwany pewnikiem Euklidesa. | ||
W naszych rozważaniach będziemy zajmować się szczególnym przypadkiem geometrii zwanej geometrią wykreślną. Geometria wykreślna, której przedmiotem są metody odwzorowań obiektów przestrzennych na płaszczyźnie, jest teoretyczna podstawą sporządzania graficznych zapisów konstrukcji stosowanych w technice. Nauka o rzutowaniu jest przedmiotem niniejszego wykładu | W naszych rozważaniach będziemy zajmować się szczególnym przypadkiem geometrii zwanej geometrią wykreślną. Geometria wykreślna, której przedmiotem są metody odwzorowań obiektów przestrzennych na płaszczyźnie, jest teoretyczna podstawą sporządzania graficznych zapisów konstrukcji stosowanych w technice. Nauka o rzutowaniu jest przedmiotem niniejszego wykładu | ||
| Linia 36: | Linia 36: | ||
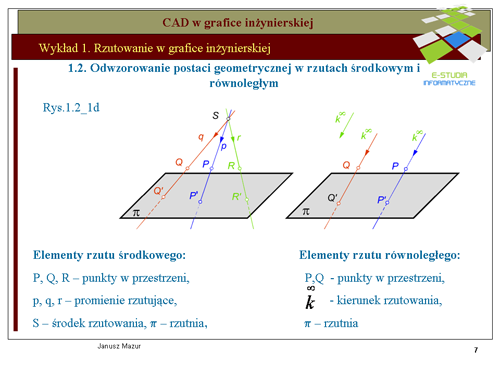
|valign="top"|Operacja odwzorowań przestrzennych opiera się o proces rzutowania. Stosowane są dwa podstawowe rodzaje rzutów stosowanych w technice. Jest to rzutowanie środkowe i rzutowanie równoległe. | |valign="top"|Operacja odwzorowań przestrzennych opiera się o proces rzutowania. Stosowane są dwa podstawowe rodzaje rzutów stosowanych w technice. Jest to rzutowanie środkowe i rzutowanie równoległe. | ||
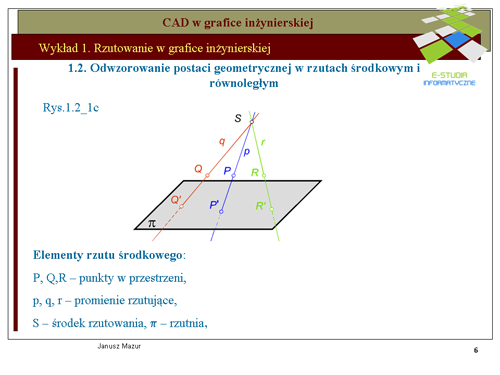
Przyjmijmy w trójwymiarowej przestrzeni euklidesowej punkt właściwy <math>S\</math>,, zwany środkiem rzutu oraz płaszczyznę <math>\pi\</math>,, zwana rzutnią. Zespół <math>R(\pi , S)</math> nazywamy aparatem projekcyjnym (elementami) rzutowania środkowego. | Przyjmijmy w trójwymiarowej przestrzeni euklidesowej punkt właściwy <math>S\ </math>,, zwany środkiem rzutu oraz płaszczyznę <math>\pi\ </math>,, zwana rzutnią. Zespół <math>R(\pi , S)</math> nazywamy aparatem projekcyjnym (elementami) rzutowania środkowego. | ||
Komputerowy zapis konstrukcji realizowany jest przy pomocy programu graficznego z grupy CAD amerykańskiej firmy Autodesk. Trzecia część wykładu realizowana jest w oparciu o graficzny program komputerowy AutoCAD Pl. | Komputerowy zapis konstrukcji realizowany jest przy pomocy programu graficznego z grupy CAD amerykańskiej firmy Autodesk. Trzecia część wykładu realizowana jest w oparciu o graficzny program komputerowy AutoCAD Pl. | ||
Do każdego wykładu przygotowano ćwiczenia w postaci zadań konstrukcyjnych, pozwalających na ugruntowanie prezentowanego materiału. | Do każdego wykładu przygotowano ćwiczenia w postaci zadań konstrukcyjnych, pozwalających na ugruntowanie prezentowanego materiału. | ||
| Linia 45: | Linia 45: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:CWGI_M1_Slajd5.png]] | |valign="top" width="500px"|[[Grafika:CWGI_M1_Slajd5.png]] | ||
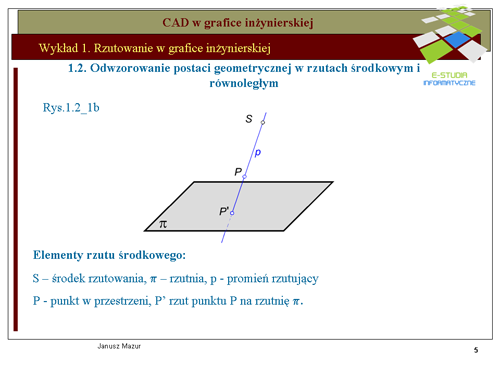
|valign="top"|Rzut środkowy punktu <math>P\</math>, otrzymano prowadząc promień rzutujący <math>p\</math>,, wychodzący ze środka rzutowania <math>S\</math>, i przechodzący przez ten punkt, aż do przecięcia się z rzutnią <math>\pi</math>Punkt przebicia promienia rzutującego z rzutnią <math>( P')</math> wyznacza rzut środkowy tego punktu. | |valign="top"|Rzut środkowy punktu <math>P\ </math>, otrzymano prowadząc promień rzutujący <math>p\ </math>,, wychodzący ze środka rzutowania <math>S\ </math>, i przechodzący przez ten punkt, aż do przecięcia się z rzutnią <math>\pi</math>Punkt przebicia promienia rzutującego z rzutnią <math>( P')</math> wyznacza rzut środkowy tego punktu. | ||
|} | |} | ||
| Linia 84: | Linia 84: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:CWGI_M1_Slajd8.png]] | |valign="top" width="500px"|[[Grafika:CWGI_M1_Slajd8.png]] | ||
|valign="top"|Zauważmy, że własności rzutu <math>G'\</math>, tworu <math>G\</math>, nie są identyczne jak własności samego tworu G. Wynika to między innymi z faktu, że twór może być bryłą przestrzenną, natomiast jego rzut równoległy zawsze jest figurą płaską. Jednak niektóre własności tworów nie ulegają zmianie po dokonaniu operacji rzutowania równoległego. Własności te nazwane zostały '''niezmiennikami rzutu równoległego'''. Niezmienniki rzutowania równoległego można opisać w sposób następujący: | |valign="top"|Zauważmy, że własności rzutu <math>G'\ </math>, tworu <math>G\ </math>, nie są identyczne jak własności samego tworu G. Wynika to między innymi z faktu, że twór może być bryłą przestrzenną, natomiast jego rzut równoległy zawsze jest figurą płaską. Jednak niektóre własności tworów nie ulegają zmianie po dokonaniu operacji rzutowania równoległego. Własności te nazwane zostały '''niezmiennikami rzutu równoległego'''. Niezmienniki rzutowania równoległego można opisać w sposób następujący: | ||
'''N1. współliniowość punktów''' (rzuty punktów leżących na prostej będą leżały na rzucie tej prostej), | '''N1. współliniowość punktów''' (rzuty punktów leżących na prostej będą leżały na rzucie tej prostej), | ||
| Linia 114: | Linia 114: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:CWGI_M1_Slajd9.png]] | |valign="top" width="500px"|[[Grafika:CWGI_M1_Slajd9.png]] | ||
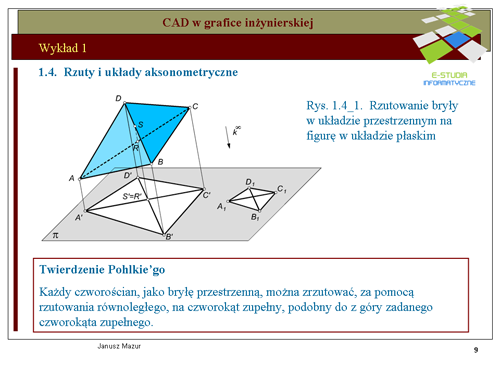
|valign="top"|Znany z geometrii elementarnej układ osi współrzędnych, zwany układem kartezjańskim, jest układem przestrzennym i składa się z osi <math> x, y, z</math> oraz początku układu współrzędnych 0. Osie przecinają się w punkcie początkowym każdej z nich pod kątami <math>90^o\</math>, względem siebie. Umieszczony w takim układzie punkt <math>P\</math>, będzie miał współrzędne <math>P(x_o, y_o, z_o)</math>. Analogicznie można zdefiniować położenie wektora i innych elementów w przestrzeni. Rzuty aksonometryczne są formą rzutów równoległych, które pozwalają przetransponować układ przestrzenny <math>0xyz</math> na układ płaski, a więc układ umożliwiający odwzorowanie tworów przestrzennych na płaszczyźnie. Takim zagadnieniem jesteśmy zainteresowani z punktu widzenia graficznego zapisu konstrukcji. Rozwijając teorię rzutowania równoległego przyjmiemy twierdzenie '''Pohlke'go''', które otworzy możliwości wyodrębnionego zapisu tworów przestrzennych zwanego '''rzutem aksonometrycznym'''. Twierdzenie to umożliwia przenoszenie brył przestrzennych do zupełnie dowolnych układów płaskich zwanych układami aksonometrycznymi. Stanowi to dla inżyniera źródło możliwości różnorodnego eksponowania swoich twórczych projektów. | |valign="top"|Znany z geometrii elementarnej układ osi współrzędnych, zwany układem kartezjańskim, jest układem przestrzennym i składa się z osi <math>x, y, z</math> oraz początku układu współrzędnych 0. Osie przecinają się w punkcie początkowym każdej z nich pod kątami <math>90^o\ </math>, względem siebie. Umieszczony w takim układzie punkt <math>P\ </math>, będzie miał współrzędne <math>P(x_o, y_o, z_o)</math>. Analogicznie można zdefiniować położenie wektora i innych elementów w przestrzeni. Rzuty aksonometryczne są formą rzutów równoległych, które pozwalają przetransponować układ przestrzenny <math>0xyz</math> na układ płaski, a więc układ umożliwiający odwzorowanie tworów przestrzennych na płaszczyźnie. Takim zagadnieniem jesteśmy zainteresowani z punktu widzenia graficznego zapisu konstrukcji. Rozwijając teorię rzutowania równoległego przyjmiemy twierdzenie '''Pohlke'go''', które otworzy możliwości wyodrębnionego zapisu tworów przestrzennych zwanego '''rzutem aksonometrycznym'''. Twierdzenie to umożliwia przenoszenie brył przestrzennych do zupełnie dowolnych układów płaskich zwanych układami aksonometrycznymi. Stanowi to dla inżyniera źródło możliwości różnorodnego eksponowania swoich twórczych projektów. | ||
| Linia 125: | Linia 125: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:CWGI_M1_Slajd10.png]][[Grafika:CWGI_M1_Slajd11.png]][[Grafika:CWGI_M1_Slajd12.png]] | |valign="top" width="500px"|[[Grafika:CWGI_M1_Slajd10.png]][[Grafika:CWGI_M1_Slajd11.png]][[Grafika:CWGI_M1_Slajd12.png]] | ||
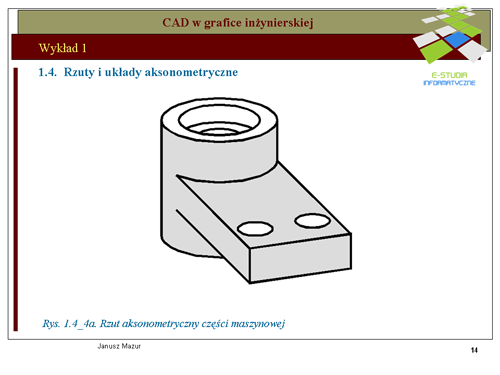
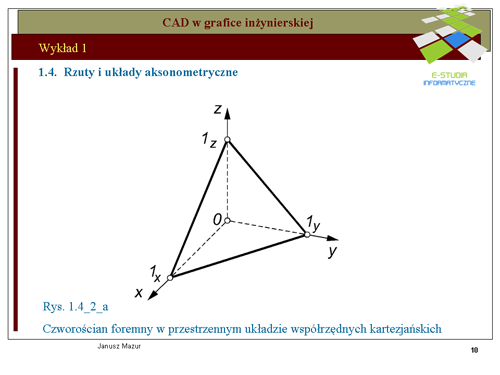
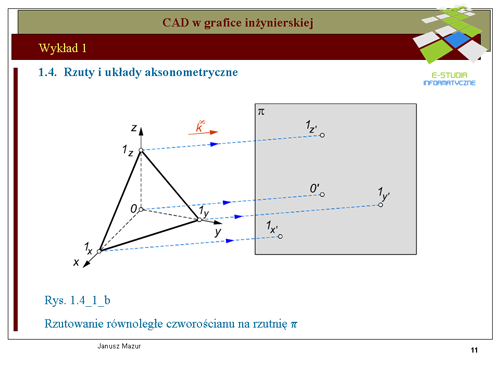
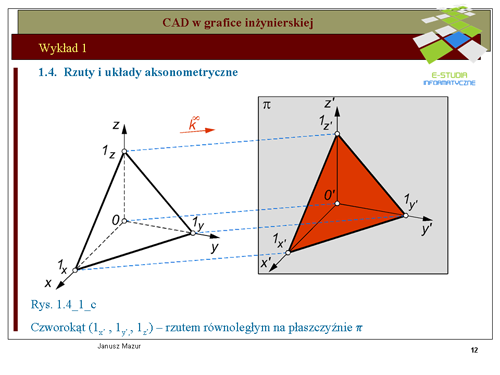
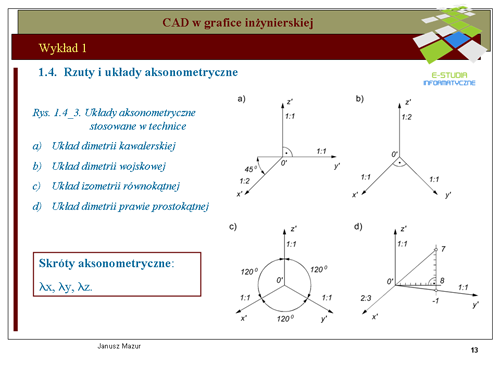
|valign="top"|Przyjmując do wiadomości ustalenia twierdzenia Pohlke'go można układ współrzędnych kartezjańskich, za pomocą rzutu równoległego, przetransponować na dowolny układ płaski. Ilustruje to rys.1.4a- 1.4c. Początek <math>0\</math>, układu <math>0xyz\</math>, oraz punkty jednostkowe <math>1x, 1y, 1z</math>, tworzą, bowiem czworościan 01x1y1z, który w myśl twierdzenia Pohlke’go można odwzorować na czworokąt zupełny <math>0’1x’1y’1z’</math>, podobny do z góry zadanego czworokąta zupełnego (czyli czworokąt dowolny). | |valign="top"|Przyjmując do wiadomości ustalenia twierdzenia Pohlke'go można układ współrzędnych kartezjańskich, za pomocą rzutu równoległego, przetransponować na dowolny układ płaski. Ilustruje to rys.1.4a- 1.4c. Początek <math>0\ </math>, układu <math>0xyz\ </math>, oraz punkty jednostkowe <math>1x, 1y, 1z</math>, tworzą, bowiem czworościan 01x1y1z, który w myśl twierdzenia Pohlke’go można odwzorować na czworokąt zupełny <math>0’1x’1y’1z’</math>, podobny do z góry zadanego czworokąta zupełnego (czyli czworokąt dowolny). | ||
Ma to fundamentalne znaczenie dla konstruktorów. Oznacza, iż odwzorowanie przestrzennych brył na płaszczyznę można dokonywać w dowolnych układach równoległego rzutu aksonometrycznego, pod warunkiem opisania podstawowych jego parametrów, do których należą rozmieszczenie rzutów osi układu kartezjańskiego oraz tzw. skrótów aksonometrycznych wynikających z rzutowania równoległego układu. | Ma to fundamentalne znaczenie dla konstruktorów. Oznacza, iż odwzorowanie przestrzennych brył na płaszczyznę można dokonywać w dowolnych układach równoległego rzutu aksonometrycznego, pod warunkiem opisania podstawowych jego parametrów, do których należą rozmieszczenie rzutów osi układu kartezjańskiego oraz tzw. skrótów aksonometrycznych wynikających z rzutowania równoległego układu. | ||
| Linia 146: | Linia 146: | ||
W układzie dimetrii kawalerskiej osie <math>y' i z'</math> położone są względem siebie pod kątem <math>90^o\</math>, . Oś <math>x'\</math>, tworzy kąt <math>135^o</math> z osiami <math>y' i z'</math>. Układ umożliwia zapis bez zniekształceń w pł. <math>(0, y', z')</math>. | W układzie dimetrii kawalerskiej osie <math>y' i z'</math> położone są względem siebie pod kątem <math>90^o\ </math>, . Oś <math>x'\ </math>, tworzy kąt <math>135^o</math> z osiami <math>y' i z'</math>. Układ umożliwia zapis bez zniekształceń w pł. <math>(0, y', z')</math>. | ||
W układzie dimetrii wojskowej oś <math>z'\</math>, układu jest pionowa, skrót zmniejsza wymiary w tym kierunku dwukrotnie. Osie <math>x', y'</math> tworzą kąt <math>135^o\</math>, z osią <math>z'\</math>,. Skróty nie zmieniają wymiarów w kierunku tych osi. | W układzie dimetrii wojskowej oś <math>z'\ </math>, układu jest pionowa, skrót zmniejsza wymiary w tym kierunku dwukrotnie. Osie <math>x', y'</math> tworzą kąt <math>135^o\ </math>, z osią <math>z'\ </math>,. Skróty nie zmieniają wymiarów w kierunku tych osi. | ||
Układ izometrii równokątnej jest układem regularnym. Osie <math>x', y', z'</math> tworzą kąt <math>120^o</math> względem siebie. Skróty nie zmieniają wymiarów w każdej osi. | Układ izometrii równokątnej jest układem regularnym. Osie <math>x', y', z'</math> tworzą kąt <math>120^o</math> względem siebie. Skróty nie zmieniają wymiarów w każdej osi. | ||
Tworzenie trzech pierwszych układów nie sprawia żadnych problemów. Komentarza wymaga tworzenie układu dimetrii prawie prostokątnej. Oś <math>z'\</math>, jest osią pionową. Pozostałe osie <math>x' i y'</math> tworzymy w sposób następujący: | Tworzenie trzech pierwszych układów nie sprawia żadnych problemów. Komentarza wymaga tworzenie układu dimetrii prawie prostokątnej. Oś <math>z'\ </math>, jest osią pionową. Pozostałe osie <math>x' i y'</math> tworzymy w sposób następujący: | ||
1. na pomocniczej linii poziomej odmierzamy osiem odcinków jednostkowych otrzymując na niej | 1. na pomocniczej linii poziomej odmierzamy osiem odcinków jednostkowych otrzymując na niej | ||
| Linia 188: | Linia 188: | ||
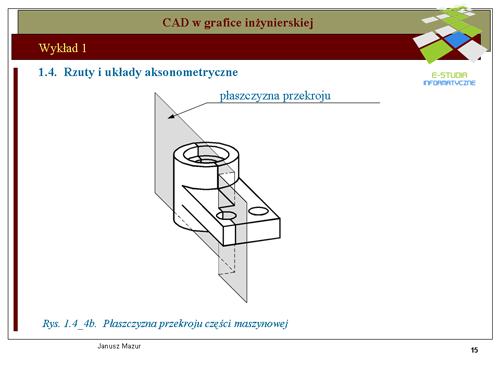
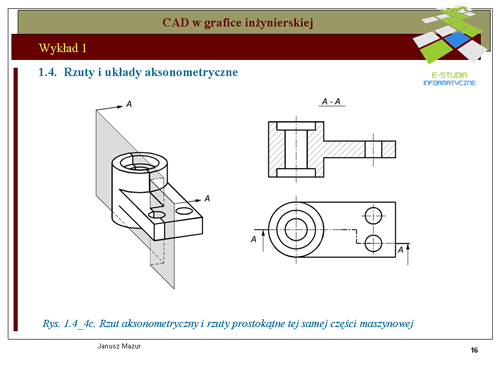
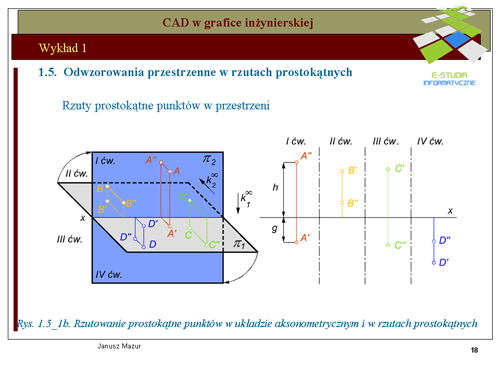
|valign="top"|Rzutowanie prostokątne elementów przestrzennych jest podstawową formą odwzorowań stosowanych w grafice inżynierskiej. Zastosowanie trzech wzajemnie prostopadłych rzutni umożliwia jednoznaczne odwzorowanie elementów przestrzennych na płaszczyźnie i odwrotnie. Tego typu rzutowanie jest podstawą '''graficznego i komputerowego zapisu konstrukcji'''. Rzut prostokątny jest rodzajem rzutu równoległego. Zatem znane są zasady rzutowania prostokątnego. Umieszczony twór przestrzenny rzutowany jest za pomocą promieni rzutujących prostopadłych do rzutni. | |valign="top"|Rzutowanie prostokątne elementów przestrzennych jest podstawową formą odwzorowań stosowanych w grafice inżynierskiej. Zastosowanie trzech wzajemnie prostopadłych rzutni umożliwia jednoznaczne odwzorowanie elementów przestrzennych na płaszczyźnie i odwrotnie. Tego typu rzutowanie jest podstawą '''graficznego i komputerowego zapisu konstrukcji'''. Rzut prostokątny jest rodzajem rzutu równoległego. Zatem znane są zasady rzutowania prostokątnego. Umieszczony twór przestrzenny rzutowany jest za pomocą promieni rzutujących prostopadłych do rzutni. | ||
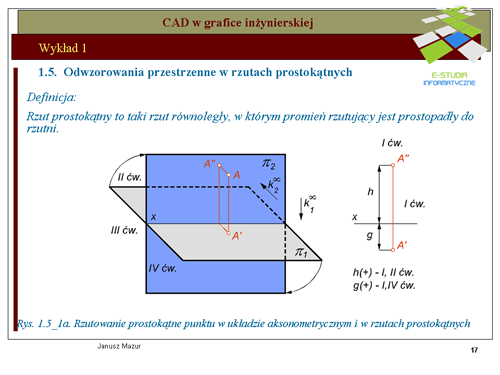
Na rys. rys. 1.5_1a przedstawiono zasady tworzenia rzutu prostokątnego punktu A w układzie dwu rzutni wzajemnie do siebie prostopadłych. Zasadę tworzenia rzutów prostokątnych przedstawiono również w rzutach aksonometrycznych, w celu pełniejszego zrozumienia omawianego zagadnienia. Rzutowanie prostokątne polega na generacji promieni rzutujących prostopadłych do rzutni, przez elementy tworów przestrzennych (w tym przypadku – punktu<math> A\</math>,) | Na rys. rys. 1.5_1a przedstawiono zasady tworzenia rzutu prostokątnego punktu A w układzie dwu rzutni wzajemnie do siebie prostopadłych. Zasadę tworzenia rzutów prostokątnych przedstawiono również w rzutach aksonometrycznych, w celu pełniejszego zrozumienia omawianego zagadnienia. Rzutowanie prostokątne polega na generacji promieni rzutujących prostopadłych do rzutni, przez elementy tworów przestrzennych (w tym przypadku – punktu<math>A\ </math>,) | ||
|} | |} | ||
| Linia 196: | Linia 196: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:CWGI_M1_Slajd18.png]] | |valign="top" width="500px"|[[Grafika:CWGI_M1_Slajd18.png]] | ||
|valign="top"|Przestrzeń <math>E^3\</math>, podzielona została na cztery obszary zwane ćwiartkami za pomocą dwóch przecinających się płaszczyzn - pionowej i poziomej. Płaszczyzny te po złożeniu do jednej płaszczyzny pozwalają nas jasne i jednoznaczne odwzorowania przestrzenne na płaszczyźnie rysunku. | |valign="top"|Przestrzeń <math>E^3\ </math>, podzielona została na cztery obszary zwane ćwiartkami za pomocą dwóch przecinających się płaszczyzn - pionowej i poziomej. Płaszczyzny te po złożeniu do jednej płaszczyzny pozwalają nas jasne i jednoznaczne odwzorowania przestrzenne na płaszczyźnie rysunku. | ||
'''ćwiartka I''' jest obszarem położonym przed rzutnią pionową i nad rzutnią poziomą, | '''ćwiartka I''' jest obszarem położonym przed rzutnią pionową i nad rzutnią poziomą, | ||
| Linia 226: | Linia 226: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:CWGI_M1_Slajd21.png]][[Grafika:CWGI_M1_Slajd22.png]] | |valign="top" width="500px"|[[Grafika:CWGI_M1_Slajd21.png]][[Grafika:CWGI_M1_Slajd22.png]] | ||
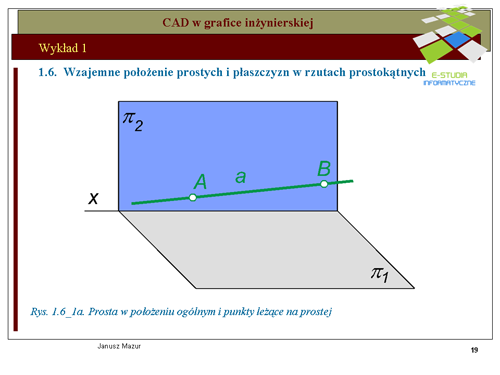
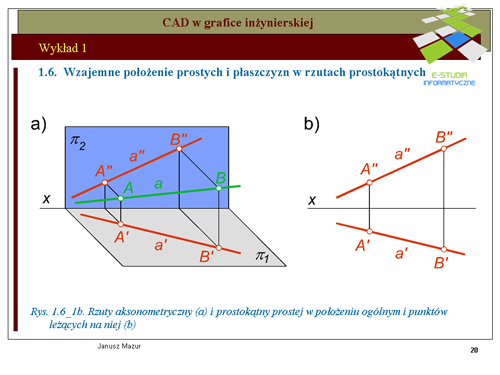
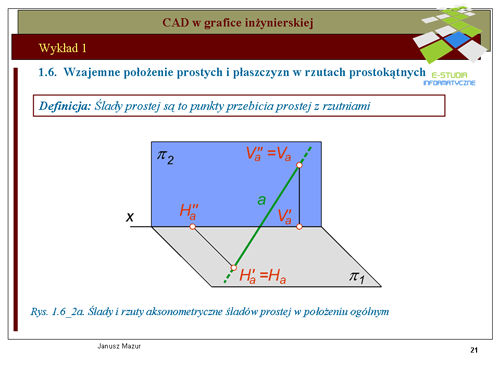
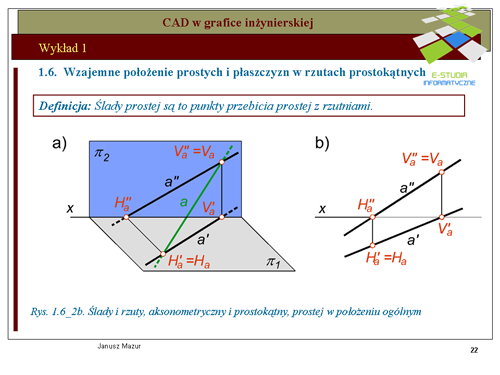
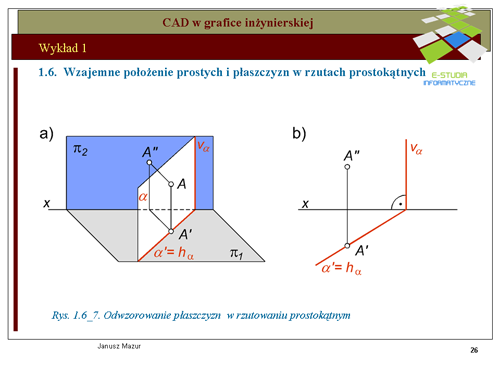
|valign="top"|Prosta określona jednoznacznie za pomocą dwóch punktów może być określona w rzutach za pomocą rzutów punktów o szczególnym położeniu względem rzutni. Takimi punktami są ś'''lady prostej. Śladami prostej''' nazywamy punkty przebicia prostej z rzutniami. Zatem możemy mówić o śladzie pionowym prostej opisywanym literą <math>V_a\</math>, (od słowa vertical) oraz o śladzie poziomym <math>H_a\</math>, (od słowa horizontal). Punkty <math>V_a i H_a</math> w rzutach określone są za pomocą ich rzutów pionowych i poziomych. Rzut pionowy śladu pionowego <math>Va''</math> pokrywa się ze śladem pionowym natomiast rzut poziomy tego śladu <math>Va'</math> znajduje się na osi <math>x\</math>, (rzuty poziome wszystkich punktów leżących na rzutni pionowej znajdują się na osi x). Rzut poziomy śladu poziomego Ha' pokrywa się ze śladem poziomym, natomiast rzut pionowy tego śladu Ha'' znajduje się na osi x (rzuty pionowe wszystkich punktów leżących na rzutni poziomej znajdują się na osi <math>x\</math>,). Rzuty prostej wraz z jej śladami przedstawiono na rys. 1.6_2a i 1.6_2b. Przedstawione rzuty prostej dotyczą jej położenia ogólnego. | |valign="top"|Prosta określona jednoznacznie za pomocą dwóch punktów może być określona w rzutach za pomocą rzutów punktów o szczególnym położeniu względem rzutni. Takimi punktami są ś'''lady prostej. Śladami prostej''' nazywamy punkty przebicia prostej z rzutniami. Zatem możemy mówić o śladzie pionowym prostej opisywanym literą <math>V_a\ </math>, (od słowa vertical) oraz o śladzie poziomym <math>H_a\ </math>, (od słowa horizontal). Punkty <math>V_a i H_a</math> w rzutach określone są za pomocą ich rzutów pionowych i poziomych. Rzut pionowy śladu pionowego <math>Va''</math> pokrywa się ze śladem pionowym natomiast rzut poziomy tego śladu <math>Va'</math> znajduje się na osi <math>x\ </math>, (rzuty poziome wszystkich punktów leżących na rzutni pionowej znajdują się na osi x). Rzut poziomy śladu poziomego Ha' pokrywa się ze śladem poziomym, natomiast rzut pionowy tego śladu Ha'' znajduje się na osi x (rzuty pionowe wszystkich punktów leżących na rzutni poziomej znajdują się na osi <math>x\ </math>,). Rzuty prostej wraz z jej śladami przedstawiono na rys. 1.6_2a i 1.6_2b. Przedstawione rzuty prostej dotyczą jej położenia ogólnego. | ||
|} | |} | ||
| Linia 235: | Linia 235: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:CWGI_M1_Slajd23.png]] | |valign="top" width="500px"|[[Grafika:CWGI_M1_Slajd23.png]] | ||
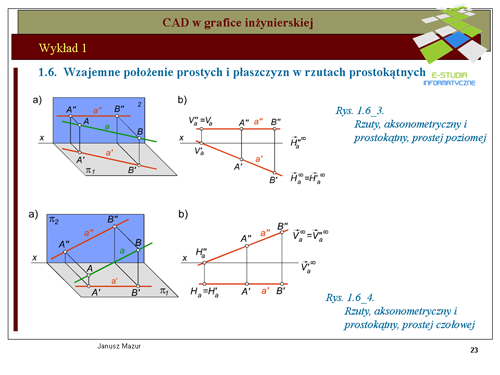
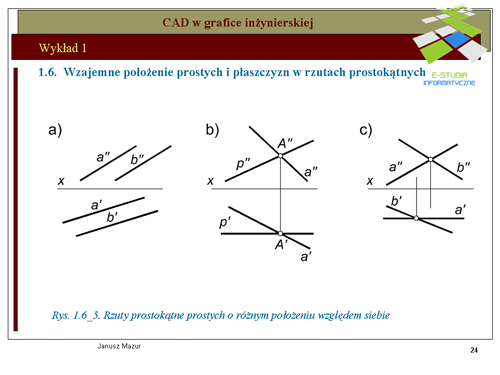
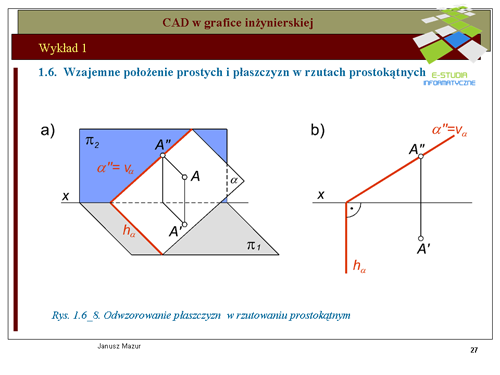
|valign="top"|W konstrukcjach przestrzennych często wykorzystywane są inne, szczególne położenia prostych, których rzuty można łatwo przewidzieć, bez konieczności żmudnych konstrukcji pomocniczych. Do takiego położenia prostych można zaliczyć np. proste poziome (równoległe do rzutni poziomej <math>\pi_1\</math>, oraz proste czołowe (równoległe do rzutni pionowej <math>\pi_2\</math>, Rzuty prostych w położeniu szczególnym przedstawiono na rys.1.6_3 i 1.6_4. Proste szczególne charakteryzują się tym, iż jeden z rzutów jest zawsze równoległy do osi x (prostej poziomej rzut poziomy i prostej czołowej rzut pionowy). Taki parametr ułatwia realizację konstrukcji z zastosowaniem prostych szczególnych, albowiem znany jest kierunek jednego z rzutów (można pominąć konstrukcje pomocnicze wyznaczające rzuty prostej pomocniczej). | |valign="top"|W konstrukcjach przestrzennych często wykorzystywane są inne, szczególne położenia prostych, których rzuty można łatwo przewidzieć, bez konieczności żmudnych konstrukcji pomocniczych. Do takiego położenia prostych można zaliczyć np. proste poziome (równoległe do rzutni poziomej <math>\pi_1\ </math>, oraz proste czołowe (równoległe do rzutni pionowej <math>\pi_2\ </math>, Rzuty prostych w położeniu szczególnym przedstawiono na rys.1.6_3 i 1.6_4. Proste szczególne charakteryzują się tym, iż jeden z rzutów jest zawsze równoległy do osi x (prostej poziomej rzut poziomy i prostej czołowej rzut pionowy). Taki parametr ułatwia realizację konstrukcji z zastosowaniem prostych szczególnych, albowiem znany jest kierunek jednego z rzutów (można pominąć konstrukcje pomocnicze wyznaczające rzuty prostej pomocniczej). | ||
|} | |} | ||
Aktualna wersja na dzień 12:06, 5 wrz 2023