PEE Moduł 2: Różnice pomiędzy wersjami
m Zastępowanie tekstu – „,</math>” na „</math>,” |
m Zastępowanie tekstu – „\</math>” na „\ </math>” |
||
| (Nie pokazano 2 pośrednich wersji utworzonych przez tego samego użytkownika) | |||
| Linia 27: | Linia 27: | ||
: <math>T </math> - okres przebiegu sinusoidalnego | : <math>T </math> - okres przebiegu sinusoidalnego | ||
: <math> \omega=2\pi f </math> - pulsacja mierzona w radianach na sekundę. | : <math>\omega=2\pi f </math> - pulsacja mierzona w radianach na sekundę. | ||
Wartości chwilowe sygnałów oznaczać będziemy małą literą a wartości maksymalne, skuteczne i wielkości operatorowe dużą. | Wartości chwilowe sygnałów oznaczać będziemy małą literą a wartości maksymalne, skuteczne i wielkości operatorowe dużą. | ||
| Linia 41: | Linia 41: | ||
: <math>F=\sqrt\left \frac{1}{T} \right \int_{t_0}^{t_o+T}f^2(t)dt </math> | : <math>F=\sqrt\left \frac{1}{T} \right \int_{t_0}^{t_o+T}f^2(t)dt</math> | ||
Łatwo udowodnić, że wartość skuteczna przebiegu okresowego nie zależy od wyboru fazy początkowej. W przypadku przebiegu sinusoidalnego napięcia <math>u(t) = U_m sin(\omega t+ \psi)</math> jest równa | Łatwo udowodnić, że wartość skuteczna przebiegu okresowego nie zależy od wyboru fazy początkowej. W przypadku przebiegu sinusoidalnego napięcia <math>u(t) = U_m sin(\omega t+ \psi)</math> jest równa | ||
| Linia 399: | Linia 399: | ||
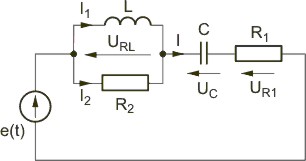
''Zadanie 2.1'' | ''Zadanie 2.1'' | ||
Wyznaczyć prądy i napięcia w obwodzie przedstawionym na rysunku. Przyjąć następujące wartości elementów: <math> e(t)=20\sqrt 2sin(100t-90^o)V, R_1=10\Omega, R_2=5\Omega, C=0,001F, L=0,05H</math>. | Wyznaczyć prądy i napięcia w obwodzie przedstawionym na rysunku. Przyjąć następujące wartości elementów: <math>e(t)=20\sqrt 2sin(100t-90^o)V, R_1=10\Omega, R_2=5\Omega, C=0,001F, L=0,05H</math>. | ||
| Linia 464: | Linia 464: | ||
Kąt fazowy przesunięcia prądu względem napięcia zasilającego jest równy <math>\varphi\</math>,. Biorąc pod uwagę, że napięcie wyprzedza prąd obwód ma charakter indukcyjny. | Kąt fazowy przesunięcia prądu względem napięcia zasilającego jest równy <math>\varphi\ </math>,. Biorąc pod uwagę, że napięcie wyprzedza prąd obwód ma charakter indukcyjny. | ||
|} | |} | ||
<hr width="100%"> | <hr width="100%"> | ||
Aktualna wersja na dzień 12:01, 5 wrz 2023

|

|
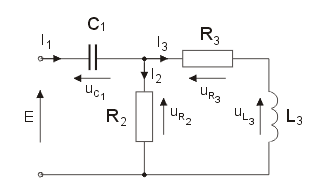
Jako przykład wyznaczymy rozpływy prądów w obwodzie z rysunku w stanie ustalonym. Przyjiemy następujące wartości parametrów: . |

|
Rozwiązanie
Wartości symboliczne elementów obwodu:
|

|
Prądy i napięcie w obwodzie:
|

|
Wartości chwilowe prądów i napięcia otzrymuje się przechodząc z wartości zespolonych na postać rzeczywista opisaną funkcją sinusoidalną według schematu przedstawionego na slajdzie 13.
|
 ] ]
|
Przedstawione powyżej zasady konstruowania przesunięć kątowych między wektorami prądu i napięcia umożliwiają podanie ogólnych zasad postępowania przy konstruowaniu wykresu wektorowego dla dowolnego obwodu RLC.
Dla cewki obowiązuje co oznacza, że napięcie na cewce wyprzedza prąd o kąt .
|
 ] ]
|
Podobnie napięcie na kondensatorze opóźnia się względem swojego prądu o kąt , gdyż
|

|
Wykres wektorowy z definicji uwzględnia przede wszystkim przesunięcia kątowe między poszczególnymi wektorami. Relacje ilościowe (długości) poszczególnych wektorów są mniej istotne i zwykle uwzględniane w sposób jedynie przybliżony. Wykres rozpoczyna się zwykle od końca obwodu (gałęzi najdalej położonej od źródła). Jeśli gałąź jest połączeniem szeregowym elementów rozpoczynamy od prądu tej gałęzi, a w przypadku połączenia równoległego – od napięcia. Następnie rysuje się na wykresie na przemian napięcia i prądy kolejnych gałęzi, dochodząc w ten sposób do źródła. Budowę wykresu kończy się w momencie dojścia do prądu i napięcia źródłowego obwodu. Relacja wektora prądu źródłowego względem napięcia decyduje o charakterze obwodu. Jeśli napięcie wypadkowe (źródłowe) wyprzedza prąd wypadkowy lub inaczej mówiąc prąd opóźnia się względem napięcia - obwód ma charakter indukcyjny. Jeśli natomiast napięcie opóźnia się względem prądu lub prąd wyprzedza napięcie - mówimy o charakterze pojemnościowym obwodu. Jeśli nie istnieje przesunięcie fazowe prądu wypadkowego względem napięcia (kąt fazowy równy zeru) mówimy o tzw. stanie rezonansu obwodu, lub po prostu charakterze rezystancyjnym danego obwodu. Charakter rezystancyjny obwodu może powstać nawet przy istnieniu w obwodzie indukcyjności i pojemności w przypadku gdy następuje kompensacja odpowiednich składowych indukcyjnej i pojemnościowej wektorów. Sposób postępowania przy sporządzaniu wykresów wektorowych przedstawimy na przykładzie konkretnego obwodu. |
|
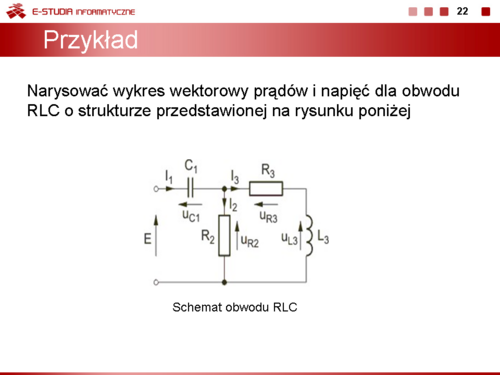
Kolejny przykład ilustruje sposób konstrukcji wykresu wektorowego prądów i napięć dla obwodu RLC o strukturze przedstawionej na rysunku:
|
|
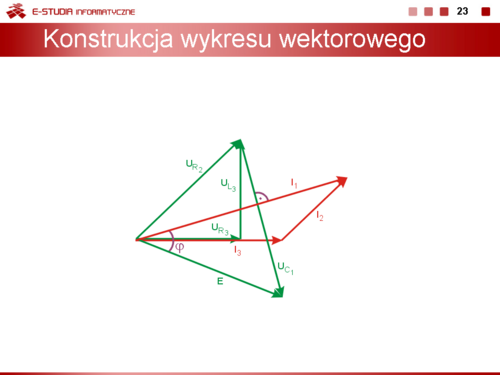
Konstrukcja wykresu wektorowego
Na rysunku obok i animacji poniżej przedstawiono wykres wektorowy prądów i napięć w obwodzie RLC z z porzedniego slajdu
|
| Zadania sprawdzające
Zadanie 2.1 Wyznaczyć prądy i napięcia w obwodzie przedstawionym na rysunku. Przyjąć następujące wartości elementów: .
Wartości symboliczne elementów obwodu:
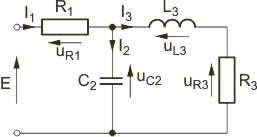
Zadanie 2.2 Sporządzić wykres wektorowy prądów i napięć w obwodzie przedstawionym na rysunku
Wykres rozpoczyna się od prądu , dodając kolejno napięcia na i , napięcie , prąd , prąd oraz napięcie . Pełny wykres wektorowy przedstawiony jest na rysunku.
|