PF Moduł 14: Różnice pomiędzy wersjami
m Zastępowanie tekstu – „,</math>” na „</math>,” |
m Zastępowanie tekstu – „\</math>” na „\ </math>” |
||
| (Nie pokazano 1 pośredniej wersji utworzonej przez tego samego użytkownika) | |||
| Linia 14: | Linia 14: | ||
|valign="top"|'''14.1 Zjawisko indukcji elektromagnetycznej''' | |valign="top"|'''14.1 Zjawisko indukcji elektromagnetycznej''' | ||
Zjawisko indukcji elektromagnetycznej odkryte przez Michaela Faradaya (1791-1867) polega na wzbudzaniu w zamkniętym obwodzie prądu indukcyjnego, pod wpływem zmian strumienia zewnętrznego pola magnetycznego. Bezpośrednią przyczyną przepływu prądu indukcyjnego jest powstająca w obwodzie siła elektromotoryczna <math>E\</math>,. | Zjawisko indukcji elektromagnetycznej odkryte przez Michaela Faradaya (1791-1867) polega na wzbudzaniu w zamkniętym obwodzie prądu indukcyjnego, pod wpływem zmian strumienia zewnętrznego pola magnetycznego. Bezpośrednią przyczyną przepływu prądu indukcyjnego jest powstająca w obwodzie siła elektromotoryczna <math>E\ </math>,. | ||
Reguła Lenza, określająca kierunek prądu indukcyjnego, wynika przede wszystkim z zasady zachowania energii. Przepływ prądu indukcyjnego jest oznaką, że w obwodzie pojawiła się energia. Zatem zmiana strumienia magnetycznego wymaga wykonania pracy przez siłę zewnętrzną, która tę zmianę wywołuje. Np. zbliżanie magnesu skierowanego biegunem '''N''' w stronę obwodu zwiększa strumień magnetyczny przenikający przez powierzchnię obwodu. Prąd indukcyjny popłynie w takim kierunku, żeby wytworzone przez niego pole magnetyczne odpychało zbliżający się magnes, a więc przed obwodem musi powstać biegun '''N'''. | Reguła Lenza, określająca kierunek prądu indukcyjnego, wynika przede wszystkim z zasady zachowania energii. Przepływ prądu indukcyjnego jest oznaką, że w obwodzie pojawiła się energia. Zatem zmiana strumienia magnetycznego wymaga wykonania pracy przez siłę zewnętrzną, która tę zmianę wywołuje. Np. zbliżanie magnesu skierowanego biegunem '''N''' w stronę obwodu zwiększa strumień magnetyczny przenikający przez powierzchnię obwodu. Prąd indukcyjny popłynie w takim kierunku, żeby wytworzone przez niego pole magnetyczne odpychało zbliżający się magnes, a więc przed obwodem musi powstać biegun '''N'''. | ||
| Linia 27: | Linia 27: | ||
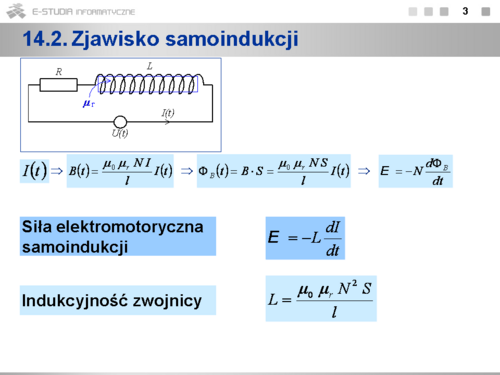
|valign="top"|'''14.2 Zjawisko samoindukcji''' | |valign="top"|'''14.2 Zjawisko samoindukcji''' | ||
Jeśli natężenie prądu płynącego w zwojnicy zmienia się w czasie <math>I(t)\</math>, , to funkcją czasu jest również wektor indukcji pola magnetycznego wytwarzanego przez ten prąd wewnątrz zwojnicy <math>B(t)\</math>, oraz wartość strumienia magnetycznego przez powierzchnię każdego zwoju <math>\Phi_B\</math>, , a więc w zwojach powstają jednakowe i zgodne siły elektromotoryczne o wartości | Jeśli natężenie prądu płynącego w zwojnicy zmienia się w czasie <math>I(t)\ </math>, , to funkcją czasu jest również wektor indukcji pola magnetycznego wytwarzanego przez ten prąd wewnątrz zwojnicy <math>B(t)\ </math>, oraz wartość strumienia magnetycznego przez powierzchnię każdego zwoju <math>\Phi_B\ </math>, , a więc w zwojach powstają jednakowe i zgodne siły elektromotoryczne o wartości | ||
:<math>E_z=-\frac{d\Phi_B}{dt}</math> | :<math>E_z=-\frac{d\Phi_B}{dt}</math> | ||
| Linia 35: | Linia 35: | ||
:<math>E=-NE_z</math> | :<math>E=-NE_z</math> | ||
Po podstawieniu i przekształceniu otrzymujemy wzór, z którego wynika zależność wartości siły elektromotorycznej samoindukcji od szybkości zmiany natężenia prądu, oraz od indukcyjności zwojnicy <math>L\</math>,, czyli współczynnika zależnego od parametrów zwojnicy, określającego zdolność zwojnicy do wytwarzania siły elektromotorycznej samoindukcji. Dużą wartość <math>L\</math>, można uzyskać dla zwojnicy o dużej liczbie zwojów, z rdzeniem ferromagnetycznym (duża wartość <math>\mu_r\</math>,). | Po podstawieniu i przekształceniu otrzymujemy wzór, z którego wynika zależność wartości siły elektromotorycznej samoindukcji od szybkości zmiany natężenia prądu, oraz od indukcyjności zwojnicy <math>L\ </math>,, czyli współczynnika zależnego od parametrów zwojnicy, określającego zdolność zwojnicy do wytwarzania siły elektromotorycznej samoindukcji. Dużą wartość <math>L\ </math>, można uzyskać dla zwojnicy o dużej liczbie zwojów, z rdzeniem ferromagnetycznym (duża wartość <math>\mu_r\ </math>,). | ||
Zjawisko samoindukcji może zachodzić w każdym obwodzie, w którym płynie prąd o zmieniającym się w czasie natężeniu. Indukcyjność <math>L\</math>, obwodu zależy od kształtu i rozmiarów obwodu oraz od obecności materiału ferromagnetycznego. | Zjawisko samoindukcji może zachodzić w każdym obwodzie, w którym płynie prąd o zmieniającym się w czasie natężeniu. Indukcyjność <math>L\ </math>, obwodu zależy od kształtu i rozmiarów obwodu oraz od obecności materiału ferromagnetycznego. | ||
|} | |} | ||
| Linia 47: | Linia 47: | ||
|valign="top"|'''14.3 Energia pola magnetycznego''' | |valign="top"|'''14.3 Energia pola magnetycznego''' | ||
W chwili <math>t_0 = 0</math> zamykamy klucz i w obwodzie RL zaczyna płynąć prąd o rosnącym natężeniu, spełniającym równanie, wynikające z drugiego prawa Kirchhoffa, którego rozwiązaniem jest funkcja <math>I(t)\</math>, , gdzie <math>\tau\</math>, jest stałą czasową procesu narastania natężenia prądu od zera do wartości wynikającej z prawa Ohma. | W chwili <math>t_0 = 0</math> zamykamy klucz i w obwodzie RL zaczyna płynąć prąd o rosnącym natężeniu, spełniającym równanie, wynikające z drugiego prawa Kirchhoffa, którego rozwiązaniem jest funkcja <math>I(t)\ </math>, , gdzie <math>\tau\ </math>, jest stałą czasową procesu narastania natężenia prądu od zera do wartości wynikającej z prawa Ohma. | ||
Pomnóżmy równanie opisujące przepływ prądu w obwodzie przez <math>I\</math>, | Pomnóżmy równanie opisujące przepływ prądu w obwodzie przez <math>I\ </math>, | ||
:<math>U_0I=LI\frac{dI}{dt}+RI^2</math> | :<math>U_0I=LI\frac{dI}{dt}+RI^2</math> | ||
| Linia 59: | Linia 59: | ||
Zatem wyrażenie <math>LI\frac{dI}{dt}=P_B=\frac{dW_B}{dt}</math> to moc w zwojnicy, czyli szybkość zmiany energii pola magnetycznego we wnętrzu zwojnicy. | Zatem wyrażenie <math>LI\frac{dI}{dt}=P_B=\frac{dW_B}{dt}</math> to moc w zwojnicy, czyli szybkość zmiany energii pola magnetycznego we wnętrzu zwojnicy. | ||
Po scałkowaniu otrzymujemy wzór określający energię pola magnetycznego <math>W_B\</math>, wewnątrz zwojnicy | Po scałkowaniu otrzymujemy wzór określający energię pola magnetycznego <math>W_B\ </math>, wewnątrz zwojnicy | ||
Wykorzystując wzory | Wykorzystując wzory | ||
| Linia 67: | Linia 67: | ||
:<math>B=\frac{\mu_0 \mu_r N}{l}I</math> | :<math>B=\frac{\mu_0 \mu_r N}{l}I</math> | ||
otrzymamy zależność energii pola magnetycznego od wartości wektora indukcji magnetycznej gdzie <math>V\</math>, jest objętością, oraz wzór określający przestrzenną gęstość energii pola magnetycznego | otrzymamy zależność energii pola magnetycznego od wartości wektora indukcji magnetycznej gdzie <math>V\ </math>, jest objętością, oraz wzór określający przestrzenną gęstość energii pola magnetycznego | ||
|} | |} | ||
| Linia 77: | Linia 77: | ||
|valign="top"|'''14.4 Elektromagnetyczne drgania swobodne''' | |valign="top"|'''14.4 Elektromagnetyczne drgania swobodne''' | ||
Modelowym układem fizycznym, w którym zachodzić mogą elektromagnetyczne drgania harmoniczne swobodne jest zamknięty obwód elektryczny o oporności równej zeru, zawierający zwojnicę o indukcyjności <math>L\</math>, i kondensator o pojemności <math>C\</math>,. | Modelowym układem fizycznym, w którym zachodzić mogą elektromagnetyczne drgania harmoniczne swobodne jest zamknięty obwód elektryczny o oporności równej zeru, zawierający zwojnicę o indukcyjności <math>L\ </math>, i kondensator o pojemności <math>C\ </math>,. | ||
W obwodzie przedstawionym na rysunku kondensator został naładowany ładunkiem <math>q_0\</math>,. Gdy w chwili <math>t=0</math> zamkniemy obwód, to kondensator zacznie się rozładowywać i zmieniający się prąd rozładowania spowoduje powstanie w zwojnicy siły elektromotorycznej samoindukcji. Stan fizyczny obwodu można opisać za pomocą II prawa Kirchhoffa. | W obwodzie przedstawionym na rysunku kondensator został naładowany ładunkiem <math>q_0\ </math>,. Gdy w chwili <math>t=0</math> zamkniemy obwód, to kondensator zacznie się rozładowywać i zmieniający się prąd rozładowania spowoduje powstanie w zwojnicy siły elektromotorycznej samoindukcji. Stan fizyczny obwodu można opisać za pomocą II prawa Kirchhoffa. | ||
Po podstawieniach i przekształceniach otrzymujemy '''równanie elektromagnetycznego oscylatora harmonicznego swobodnego.''' | Po podstawieniach i przekształceniach otrzymujemy '''równanie elektromagnetycznego oscylatora harmonicznego swobodnego.''' | ||
Rozwiązaniem tego równania, spełniającym warunki początkowe: <math>q(0) = q_0</math> , <math>I(0) = 0</math> jest funkcja <math>q(t)\</math>, , gdzie <math>\omega_0\</math>, - '''częstość drgań swobodnych''' , gdzie <math>\omega_0 t\</math>, - faza drgań, <math>q(0)\</math>, - amplituda drgań. | Rozwiązaniem tego równania, spełniającym warunki początkowe: <math>q(0) = q_0</math> , <math>I(0) = 0</math> jest funkcja <math>q(t)\ </math>, , gdzie <math>\omega_0\ </math>, - '''częstość drgań swobodnych''' , gdzie <math>\omega_0 t\ </math>, - faza drgań, <math>q(0)\ </math>, - amplituda drgań. | ||
Mając funkcję <math>q(t)\</math>, można obliczyć napięcie na kondensatorze <math>U_C(t)\</math>,, natężenie prądu <math>I(t)\</math>, oraz napięcie na zwojnicy <math>U_L(t)\</math>,. | Mając funkcję <math>q(t)\ </math>, można obliczyć napięcie na kondensatorze <math>U_C(t)\ </math>,, natężenie prądu <math>I(t)\ </math>, oraz napięcie na zwojnicy <math>U_L(t)\ </math>,. | ||
Warto zauważyć, że napięcia na kondensatorze i zwojnicy mają równe amplitudy i przeciwne fazy (przesunięcie fazowe wynosi <math>-\pi\</math>,), zaś natężenie prądu jest przesunięte w fazie o <math>-\pi/2\</math>,. | Warto zauważyć, że napięcia na kondensatorze i zwojnicy mają równe amplitudy i przeciwne fazy (przesunięcie fazowe wynosi <math>-\pi\ </math>,), zaś natężenie prądu jest przesunięte w fazie o <math>-\pi/2\ </math>,. | ||
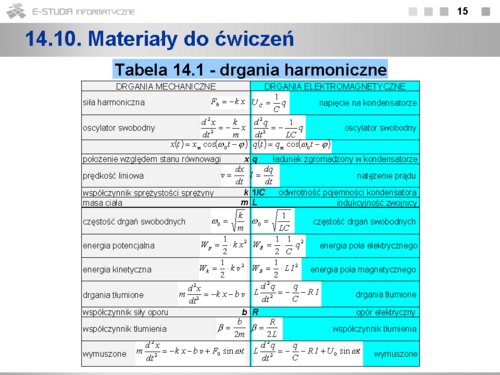
Z powyższej analizy wynika, że po dostarczeniu do obwodu LC porcji energii (naładowanie kondensatora) i braku dalszej ingerencji zewnętrznej, zachodzą w nim drgania harmoniczne swobodne - wielkości opisujące stan układu są funkcjami harmonicznymi. Porównanie z mechanicznym oscylatorem harmonicznym swobodnym (np. klocek o masie m zaczepiony do sprężyny o współczynniku sprężystości k) pokazuje, że ładunek na kondensatorze jest wielkością analogiczną do wychylenia z położenia równowagi a natężenie prądu do prędkości. Pełne zestawienie analogii między drganiami elektromagnetycznymi i drganiami mechanicznymi przedstawiono w tabeli nr 14.1. | Z powyższej analizy wynika, że po dostarczeniu do obwodu LC porcji energii (naładowanie kondensatora) i braku dalszej ingerencji zewnętrznej, zachodzą w nim drgania harmoniczne swobodne - wielkości opisujące stan układu są funkcjami harmonicznymi. Porównanie z mechanicznym oscylatorem harmonicznym swobodnym (np. klocek o masie m zaczepiony do sprężyny o współczynniku sprężystości k) pokazuje, że ładunek na kondensatorze jest wielkością analogiczną do wychylenia z położenia równowagi a natężenie prądu do prędkości. Pełne zestawienie analogii między drganiami elektromagnetycznymi i drganiami mechanicznymi przedstawiono w tabeli nr 14.1. | ||
| Linia 93: | Linia 93: | ||
'''Okres <math>T_0=2\pi/{\omega}</math> i częstotliwość drgań swobodnych <math>\nu_0=1/T_0</math>''' (inaczej drgań własnych) obwodu LC zależą od pojemności i indukcyjności obwodu. | '''Okres <math>T_0=2\pi/{\omega}</math> i częstotliwość drgań swobodnych <math>\nu_0=1/T_0</math>''' (inaczej drgań własnych) obwodu LC zależą od pojemności i indukcyjności obwodu. | ||
Przejdźmy teraz do rozważań energetycznych. Iloczyn napięcia i natężenia prądu jest równy mocy, a zatem możemy obliczyć moc <math>P_E\</math>, i energię <math>W_E\</math>, pola elektrycznego w kondensatorze | Przejdźmy teraz do rozważań energetycznych. Iloczyn napięcia i natężenia prądu jest równy mocy, a zatem możemy obliczyć moc <math>P_E\ </math>, i energię <math>W_E\ </math>, pola elektrycznego w kondensatorze | ||
:<math>P_E=\frac{W_E}{dt}=U_C I=\frac{q}{C}\cdot I</math> | :<math>P_E=\frac{W_E}{dt}=U_C I=\frac{q}{C}\cdot I</math> | ||
| Linia 99: | Linia 99: | ||
:<math>W_E=\int \frac{q}{C}dq=\frac{1}{2C}\cdot q^2=\frac{1}{2C}\cdot q_{0}^2cos^2\omega_0 t</math> | :<math>W_E=\int \frac{q}{C}dq=\frac{1}{2C}\cdot q^2=\frac{1}{2C}\cdot q_{0}^2cos^2\omega_0 t</math> | ||
oraz moc <math>P_B\</math>, i energię <math>W_B\</math>, pola magnetycznego w zwojnicy | oraz moc <math>P_B\ </math>, i energię <math>W_B\ </math>, pola magnetycznego w zwojnicy | ||
:<math>P_B=\frac{W_B}{dt}=U_L I=L\frac{dI}{dt}\cdot I</math> | :<math>P_B=\frac{W_B}{dt}=U_L I=L\frac{dI}{dt}\cdot I</math> | ||
| Linia 105: | Linia 105: | ||
:<math>W_B=\int LIdI=\frac{1}{2}LI^2=\frac{1}{2C}\cdot q_{0}^2sin^2\omega_0 t</math> | :<math>W_B=\int LIdI=\frac{1}{2}LI^2=\frac{1}{2C}\cdot q_{0}^2sin^2\omega_0 t</math> | ||
Jak widać energie pól w kondensatorze i w zwojnicy mają takie same amplitudy, ale są przesunięte w fazie o <math>\pi/2\</math>,. Całkowita energia układu drgającego będąca sumą energii pola elektrycznego w kondensatorze i pola magnetycznego w zwojnicy | Jak widać energie pól w kondensatorze i w zwojnicy mają takie same amplitudy, ale są przesunięte w fazie o <math>\pi/2\ </math>,. Całkowita energia układu drgającego będąca sumą energii pola elektrycznego w kondensatorze i pola magnetycznego w zwojnicy | ||
Z powyższych rozważań wynika, że elektromagnetyczne drgania swobodne w obwodzie LC można traktować jak okresowe przemiany energii pola elektrycznego w kondensatorze w energię pola magnetycznego w zwojnicy i na odwrót. Okres tych przemian jest równy połowie okresu drgań własnych czyli okresu zmienności napięć na kondensatorze i zwojnicy oraz natężenia prądu. W rzeczywistych obwodach elektrycznych występuje zawsze niezerowy opór elektryczny, a więc wydziela się energia cieplna. W takim przypadku energia układu drgającego maleje i po pewnym czasie drgania zanikają. | Z powyższych rozważań wynika, że elektromagnetyczne drgania swobodne w obwodzie LC można traktować jak okresowe przemiany energii pola elektrycznego w kondensatorze w energię pola magnetycznego w zwojnicy i na odwrót. Okres tych przemian jest równy połowie okresu drgań własnych czyli okresu zmienności napięć na kondensatorze i zwojnicy oraz natężenia prądu. W rzeczywistych obwodach elektrycznych występuje zawsze niezerowy opór elektryczny, a więc wydziela się energia cieplna. W takim przypadku energia układu drgającego maleje i po pewnym czasie drgania zanikają. | ||
| Linia 117: | Linia 117: | ||
|valign="top"|'''14.5 Elektromagnetyczne drgania tłumione''' | |valign="top"|'''14.5 Elektromagnetyczne drgania tłumione''' | ||
Drgania harmoniczne tłumione mogą zachodzić w obwodach elektrycznych zawierających elementy <math>R, L, C\</math>,. | Drgania harmoniczne tłumione mogą zachodzić w obwodach elektrycznych zawierających elementy <math>R, L, C\ </math>,. | ||
Załóżmy, że naładowany kondensator o pojemności <math>C\</math>, zaczyna się rozładowywać przez opór <math>R\</math>, i zwojnicę o indukcyjności <math>L\</math>,. Zgodnie z drugim prawem Kirchoffa suma zmian potencjału na drodze zamkniętej jest równa zeru | Załóżmy, że naładowany kondensator o pojemności <math>C\ </math>, zaczyna się rozładowywać przez opór <math>R\ </math>, i zwojnicę o indukcyjności <math>L\ </math>,. Zgodnie z drugim prawem Kirchoffa suma zmian potencjału na drodze zamkniętej jest równa zeru | ||
Po podstawieniach i przekształceniach otrzymamy równanie elektromagnetycznego oscylatora harmonicznego tłumionego, w którym oprócz częstości drgań swobodnych <math>\omega_0\</math>, pojawia się współczynnik tłumienia <math>\beta\</math>,. | Po podstawieniach i przekształceniach otrzymamy równanie elektromagnetycznego oscylatora harmonicznego tłumionego, w którym oprócz częstości drgań swobodnych <math>\omega_0\ </math>, pojawia się współczynnik tłumienia <math>\beta\ </math>,. | ||
Gdy spełniony jest warunek <math>\beta <\omega_0\</math>, to rozwiązaniem tego równania różniczkowego jest funkcja “okresowa” <math>q(t)\</math>,, zatem w obwodzie zachodzić będą drgania tłumione z częstością <math>\omega_0\</math>,. | Gdy spełniony jest warunek <math>\beta <\omega_0\ </math>, to rozwiązaniem tego równania różniczkowego jest funkcja “okresowa” <math>q(t)\ </math>,, zatem w obwodzie zachodzić będą drgania tłumione z częstością <math>\omega_0\ </math>,. | ||
Na rysunku przedstawiono porównanie drgań swobodnych i tłumionych, dla kilku wartości współczynnika tłumienia. Warto zauważyć, że szybkość zaniku amplitudy drgań silnie zależy od współczynnika tłumienia <math>\beta\</math>,. Natomiast istotny wpływ na częstość drgań tłumionych pojawia się dopiero dla wartości współczynnika tłumienia <math>\beta\</math>, bliskich wartości granicznej, czyli <math>\omega_0\</math>,. | Na rysunku przedstawiono porównanie drgań swobodnych i tłumionych, dla kilku wartości współczynnika tłumienia. Warto zauważyć, że szybkość zaniku amplitudy drgań silnie zależy od współczynnika tłumienia <math>\beta\ </math>,. Natomiast istotny wpływ na częstość drgań tłumionych pojawia się dopiero dla wartości współczynnika tłumienia <math>\beta\ </math>, bliskich wartości granicznej, czyli <math>\omega_0\ </math>,. | ||
Podstawowe różnice między drganiami tłumionymi i drganiami swobdnymi: | Podstawowe różnice między drganiami tłumionymi i drganiami swobdnymi: | ||
| Linia 133: | Linia 133: | ||
*całkowita energia oscylatora maleje z upływem czasu | *całkowita energia oscylatora maleje z upływem czasu | ||
Gdy spełniony jest warunek <math>\beta \ge \omega_0\</math>, rozwiązaniem równania różniczkowego jest funkcja aperiodyczna. Rozładowanie kondensatora jest eksponencjalne i jednorazowe. | Gdy spełniony jest warunek <math>\beta \ge \omega_0\ </math>, rozwiązaniem równania różniczkowego jest funkcja aperiodyczna. Rozładowanie kondensatora jest eksponencjalne i jednorazowe. | ||
|} | |} | ||
| Linia 143: | Linia 143: | ||
|valign="top"|'''14.6 Elektromagnetyczne drgania wymuszone''' | |valign="top"|'''14.6 Elektromagnetyczne drgania wymuszone''' | ||
Elektromagnetyczne drgania wymuszone można zaobserować w obwodzie RLC (zawierającym zwojnicę o indukcyjności <math>L\</math>,, kondensator o pojemności <math>C\</math>, oraz opornik o oporności <math>R\</math>,) do którego dołączone zostało źródło napięcia sinusoidalnego. | Elektromagnetyczne drgania wymuszone można zaobserować w obwodzie RLC (zawierającym zwojnicę o indukcyjności <math>L\ </math>,, kondensator o pojemności <math>C\ </math>, oraz opornik o oporności <math>R\ </math>,) do którego dołączone zostało źródło napięcia sinusoidalnego. | ||
Stan fizyczny tego układu opisuje w dowolnej chwili II prawo Kirchhoffa. Po podstawieniach i przekształceniach , otrzymujemy '''równanie elektromagnetycznych drgań wymuszonych.''' W równaniu tym bezpośrednie parametry układu fizycznego jakimi są w przypadku obwodu RLC: indukcyjność <math>L\</math>,, pojemność <math>C\</math>, i oporność <math>R\</math>, zostały zastąpione przez uniwersalne parametry występujące w opisie drgań harmonicznych dowolnego układu fizycznego (np. oscylator harmoniczny mechaniczny), a mianowicie przez częstość drgań własnych <math>\omega_0\</math>, i współczynnik tłumienia <math>\beta\</math>,. | Stan fizyczny tego układu opisuje w dowolnej chwili II prawo Kirchhoffa. Po podstawieniach i przekształceniach , otrzymujemy '''równanie elektromagnetycznych drgań wymuszonych.''' W równaniu tym bezpośrednie parametry układu fizycznego jakimi są w przypadku obwodu RLC: indukcyjność <math>L\ </math>,, pojemność <math>C\ </math>, i oporność <math>R\ </math>, zostały zastąpione przez uniwersalne parametry występujące w opisie drgań harmonicznych dowolnego układu fizycznego (np. oscylator harmoniczny mechaniczny), a mianowicie przez częstość drgań własnych <math>\omega_0\ </math>, i współczynnik tłumienia <math>\beta\ </math>,. | ||
Ponieważ napięcie wymuszające jest sinusoidalną funkcją czasu, to rozwiązania tego równania poszukujemy w postaci funkcji również sinusoidalnej, a zatem przewidujemy, że ładunek na kondensatorze będzie się zmieniać z częstością taką jak częstość napięcia wymuszającego oraz, że będzie przesunięty w fazie o <math>\varphi\</math>, względem tego napięcia. Po podstawieniu przewidywanej funkcji <math>q(t)\</math>, do równania i zażądaniu aby równanie to stało się tożsamością (funkcja <math>q(t)\</math>, musi spełniać to równanie w każdej chwili czasu) otrzymamy wzory określające '''amplitudę ładunku <math>q_0\</math>,''' i '''przesunięcie fazowe <math>\varphi\</math>,''' . | Ponieważ napięcie wymuszające jest sinusoidalną funkcją czasu, to rozwiązania tego równania poszukujemy w postaci funkcji również sinusoidalnej, a zatem przewidujemy, że ładunek na kondensatorze będzie się zmieniać z częstością taką jak częstość napięcia wymuszającego oraz, że będzie przesunięty w fazie o <math>\varphi\ </math>, względem tego napięcia. Po podstawieniu przewidywanej funkcji <math>q(t)\ </math>, do równania i zażądaniu aby równanie to stało się tożsamością (funkcja <math>q(t)\ </math>, musi spełniać to równanie w każdej chwili czasu) otrzymamy wzory określające '''amplitudę ładunku <math>q_0\ </math>,''' i '''przesunięcie fazowe <math>\varphi\ </math>,''' . | ||
Przy ustalonych parametrach układu <math>R, L, C\</math>, (a więc również <math>\omega_0\</math>, i <math>\beta\</math>,) amplituda ładunku oraz przesunięcie fazowe są funkcjami częstości <math>\omega\</math>, napięcia wymuszającego. Po przeprowadzeniu badania funkcji <math>q(0)(\omega)\</math>, można stwierdzić, że amplituda ładunku na kondensatorze osiąga wartość maksymalną dla częstości wymuszania <math>\omega_r\</math>, , gdy współczynnik tłumienia jest mniejszy od wartości granicznej <math>(\beta <\beta_g)</math> . | Przy ustalonych parametrach układu <math>R, L, C\ </math>, (a więc również <math>\omega_0\ </math>, i <math>\beta\ </math>,) amplituda ładunku oraz przesunięcie fazowe są funkcjami częstości <math>\omega\ </math>, napięcia wymuszającego. Po przeprowadzeniu badania funkcji <math>q(0)(\omega)\ </math>, można stwierdzić, że amplituda ładunku na kondensatorze osiąga wartość maksymalną dla częstości wymuszania <math>\omega_r\ </math>, , gdy współczynnik tłumienia jest mniejszy od wartości granicznej <math>(\beta <\beta_g)</math> . | ||
'''Zjawisko wymuszania drgań z taką częstością przy której amplituda drgań osiąga wartość maksymalną nazywamy rezonansem.''' Rezonans w obwodzie RLC zachodzi przy częstości wymuszania <math>\omega_r\</math>, zwanej częstością rezonansową, gdy współczynnik tłumienia <math>\beta\</math>, jest mniejszy od wartości granicznej <math>\beta_g\</math>,. Gdy tłumienie jest większe <math>(\beta >\beta_g)</math> układu RLC nie udaje się wprowadzić w stan rezonansu. | '''Zjawisko wymuszania drgań z taką częstością przy której amplituda drgań osiąga wartość maksymalną nazywamy rezonansem.''' Rezonans w obwodzie RLC zachodzi przy częstości wymuszania <math>\omega_r\ </math>, zwanej częstością rezonansową, gdy współczynnik tłumienia <math>\beta\ </math>, jest mniejszy od wartości granicznej <math>\beta_g\ </math>,. Gdy tłumienie jest większe <math>(\beta >\beta_g)</math> układu RLC nie udaje się wprowadzić w stan rezonansu. | ||
Amplitudę drgań i przesunięcie fazowe w stanie rezonansu można wyrazić wzorami: | Amplitudę drgań i przesunięcie fazowe w stanie rezonansu można wyrazić wzorami: | ||
| Linia 161: | Linia 161: | ||
Szczególny przypadek rezonansu występuje w przypadku gdy współczynnik tłumienia <math>\beta = 0</math>. Dla takiego układu rezonans zachodzi przy częstości wymuszania równej częstości drgań własnych <math>\omega_r=\omega_0</math> i objawia się wzrostem amplitudy do nieskończoności oraz przesunięciem fazowym <math>\omega_r=\pi/2</math>. W takiej sytuacji dochodzi przeważnie do zniszczenia układu drgającego zanim amplituda drgań osiągnie wartość nieskończoną. | Szczególny przypadek rezonansu występuje w przypadku gdy współczynnik tłumienia <math>\beta = 0</math>. Dla takiego układu rezonans zachodzi przy częstości wymuszania równej częstości drgań własnych <math>\omega_r=\omega_0</math> i objawia się wzrostem amplitudy do nieskończoności oraz przesunięciem fazowym <math>\omega_r=\pi/2</math>. W takiej sytuacji dochodzi przeważnie do zniszczenia układu drgającego zanim amplituda drgań osiągnie wartość nieskończoną. | ||
Graniczne wartości amplitudy drgań <math>q_0\</math>, i przesunięcia fazowego dla częstości wymuszania dążącej do zera wynoszą: | Graniczne wartości amplitudy drgań <math>q_0\ </math>, i przesunięcia fazowego dla częstości wymuszania dążącej do zera wynoszą: | ||
:<math>\begin{matrix}\lim_{\omega \to 0}q_0=U_0 C &\lim_{\omega \to 0}\varphi=0 \end{matrix}</math> | :<math>\begin{matrix}\lim_{\omega \to 0}q_0=U_0 C &\lim_{\omega \to 0}\varphi=0 \end{matrix}</math> | ||
| Linia 169: | Linia 169: | ||
:<math>\begin{matrix}\lim_{\omega \to \infty}q_0=0 &\lim_{\omega \to \infty}\varphi=0 \end{matrix}</math> | :<math>\begin{matrix}\lim_{\omega \to \infty}q_0=0 &\lim_{\omega \to \infty}\varphi=0 \end{matrix}</math> | ||
Warto jeszcze zaznaczyć, że niezależnie od wartości współczynnika tłumienia, przesunięcie fazowe <math>\varphi\</math>, osiąga wartość <math>\pi/2\</math>, przy częstości wymuszania <math>\omega\</math>, równej częstości drgań własnych układu <math>\omega_0\</math>,. | Warto jeszcze zaznaczyć, że niezależnie od wartości współczynnika tłumienia, przesunięcie fazowe <math>\varphi\ </math>, osiąga wartość <math>\pi/2\ </math>, przy częstości wymuszania <math>\omega\ </math>, równej częstości drgań własnych układu <math>\omega_0\ </math>,. | ||
Wzory opisujące drgania wymuszone i rezonans można zapisać w uniwersalnej postaci bezwymiarowej, słusznej zarówno dla drgań elektromagnetycznych, jak i dla drgań mechanicznych. W tym celu wprowadza się tzw. '''parametry zredukowane''': | Wzory opisujące drgania wymuszone i rezonans można zapisać w uniwersalnej postaci bezwymiarowej, słusznej zarówno dla drgań elektromagnetycznych, jak i dla drgań mechanicznych. W tym celu wprowadza się tzw. '''parametry zredukowane''': | ||
| Linia 185: | Linia 185: | ||
:<math>w_r=\sqrt{1-2u^2}</math> | :<math>w_r=\sqrt{1-2u^2}</math> | ||
Na slajdzie przedstawiono wykresy zależności zredukowanej amplitudy drgań <math>X\</math>, od zredukowanej częstości drgań w dla kilku wartości zredukowanego współczynnika tłumienia <math>u\</math>,. W miarę wzrostu współczynnika tłumienia rezonans pojawia się dla częstości coraz mniejszych i wartość amplitudy drgań w stanie rezonansu jest coraz mniejsza. Po przekroczeniu granicznej wartości współczynnika tłumienia rezonans nie pojawia się (krzywa <math>X(w)\</math>, nie posiada maksimum). | Na slajdzie przedstawiono wykresy zależności zredukowanej amplitudy drgań <math>X\ </math>, od zredukowanej częstości drgań w dla kilku wartości zredukowanego współczynnika tłumienia <math>u\ </math>,. W miarę wzrostu współczynnika tłumienia rezonans pojawia się dla częstości coraz mniejszych i wartość amplitudy drgań w stanie rezonansu jest coraz mniejsza. Po przekroczeniu granicznej wartości współczynnika tłumienia rezonans nie pojawia się (krzywa <math>X(w)\ </math>, nie posiada maksimum). | ||
Znając funkcję <math>q(t)\</math>, można wyznaczyć pozostałe funkcje opisujące stan fizyczny układu drgającego: napięcie na kondensatorze, natężenie prądu, napięcie na oporniku oraz napięcie na zwojnicy (p. Przykład 14.2). | Znając funkcję <math>q(t)\ </math>, można wyznaczyć pozostałe funkcje opisujące stan fizyczny układu drgającego: napięcie na kondensatorze, natężenie prądu, napięcie na oporniku oraz napięcie na zwojnicy (p. Przykład 14.2). | ||
Niezależność amplitud ładunku i natężenia prądu oraz przesunięć fazowych względem napięcia wymuszającego oznacza, że zachodzą tzw. '''drgania ustalone'''. Układ fizyczny dopasowuje się do czynnika wymuszającego. Można łatwo wykazać, że podczas drgań ustalonych szybkość dostarczania energii przez źródło napięcia wymuszającego zrównuje się z szybkością strat energii na pracę prądu w oporniku i suma średniej energii pola elektrycznego w kondensatorze i średniej energii pola magnetycznego w zwojnicy jest stała (dla danej częstości wymuszania). | Niezależność amplitud ładunku i natężenia prądu oraz przesunięć fazowych względem napięcia wymuszającego oznacza, że zachodzą tzw. '''drgania ustalone'''. Układ fizyczny dopasowuje się do czynnika wymuszającego. Można łatwo wykazać, że podczas drgań ustalonych szybkość dostarczania energii przez źródło napięcia wymuszającego zrównuje się z szybkością strat energii na pracę prądu w oporniku i suma średniej energii pola elektrycznego w kondensatorze i średniej energii pola magnetycznego w zwojnicy jest stała (dla danej częstości wymuszania). | ||
| Linia 215: | Linia 215: | ||
*I prawo Maxwella (uogólnione prawo Faradaya) - wirowe pole elektryczne | *I prawo Maxwella (uogólnione prawo Faradaya) - wirowe pole elektryczne | ||
Cyrkulacja wektora natężenia pola elektrycznego wzdłuż zamkniętej krzywej <math>L\</math>, jest równa szybkości zmiany (ze znakiem ujemnym) strumienia wektora indukcji pola magnetycznego przez powierzchnię <math>S\</math>,, ograniczoną przez krzywą <math>L\</math>,. Wir pola elektrycznego jest powiązany z wektorową zmianą pola magnetycznego za pomocą reguły śruby prawoskrętnej, z uwzględnieniem znaku minus po prawej stronie równania. | Cyrkulacja wektora natężenia pola elektrycznego wzdłuż zamkniętej krzywej <math>L\ </math>, jest równa szybkości zmiany (ze znakiem ujemnym) strumienia wektora indukcji pola magnetycznego przez powierzchnię <math>S\ </math>,, ograniczoną przez krzywą <math>L\ </math>,. Wir pola elektrycznego jest powiązany z wektorową zmianą pola magnetycznego za pomocą reguły śruby prawoskrętnej, z uwzględnieniem znaku minus po prawej stronie równania. | ||
Wskutek zmiany strumienia pola magnetycznego powstaje wirowe pole elektryczne (linie sił pola są krzywymi zamkniętymi). Takie pole elektryczne jest polem bezźródłowym, tzn. w takim polu strumień wektora indukcji elektrycznej przez zamknietą powierzchnię jest równy zeru <math>\oint_{S} \overrightarrow{D}\ d\overrightarrow{S}=0</math>. | Wskutek zmiany strumienia pola magnetycznego powstaje wirowe pole elektryczne (linie sił pola są krzywymi zamkniętymi). Takie pole elektryczne jest polem bezźródłowym, tzn. w takim polu strumień wektora indukcji elektrycznej przez zamknietą powierzchnię jest równy zeru <math>\oint_{S} \overrightarrow{D}\ d\overrightarrow{S}=0</math>. | ||
| Linia 221: | Linia 221: | ||
*II prawo Maxwella (uogólnione prawo Ampere’a) - wirowe pole magnetyczne | *II prawo Maxwella (uogólnione prawo Ampere’a) - wirowe pole magnetyczne | ||
Cyrkulacja wektora natężenia pola magnetycznego wzdłuż zamkniętej krzywej <math>L\</math>, jest równa sumie natężenia prądu przepływającego przez powierzchnię <math>S\</math>,, ograniczoną przez krzywą <math>L\</math>, oraz szybkości zmiany strumienia wektora indukcji pola elektrycznego przez powierzchnię <math>S\</math>,, ograniczoną przez tę krzywą, czyli natężenia tzw. prądu przesunięcia. | Cyrkulacja wektora natężenia pola magnetycznego wzdłuż zamkniętej krzywej <math>L\ </math>, jest równa sumie natężenia prądu przepływającego przez powierzchnię <math>S\ </math>,, ograniczoną przez krzywą <math>L\ </math>, oraz szybkości zmiany strumienia wektora indukcji pola elektrycznego przez powierzchnię <math>S\ </math>,, ograniczoną przez tę krzywą, czyli natężenia tzw. prądu przesunięcia. | ||
:<math>\oint_{L} \overrightarrow{D}\cdot d\overrightarrow{l}=\int_{S} \overrightarrow{j}\cdot d\overrightarrow{S}+\frac{\partial}{\partial t}\int_{S}\overrightarrow{D}\cdot d\overrightarrow{S}</math> | :<math>\oint_{L} \overrightarrow{D}\cdot d\overrightarrow{l}=\int_{S} \overrightarrow{j}\cdot d\overrightarrow{S}+\frac{\partial}{\partial t}\int_{S}\overrightarrow{D}\cdot d\overrightarrow{S}</math> | ||
| Linia 229: | Linia 229: | ||
Wskutek przepływu prądu elektrycznego i/lub zmiany strumienia pola elektrycznego powstaje wirowe pole magnetyczne (linie wektora indukcji magnetycznej są krzywymi zamkniętymi). | Wskutek przepływu prądu elektrycznego i/lub zmiany strumienia pola elektrycznego powstaje wirowe pole magnetyczne (linie wektora indukcji magnetycznej są krzywymi zamkniętymi). | ||
Uzupełnieniem czterech zasadniczych równań Maxwella są tzw. równania materiałowe, czyli związki między wektorami opisującymi pole elektryczne, pole magnetyczne oraz przepływ prądu elektrycznego. W równaniach tych pojawiają się parametry elektryczne i magnetyczne ośrodka: względna przenikalność elektryczna <math>\varepsilon_r\</math>, i względna przenikalność magnetyczna <math>\mu_r\</math>, oraz przewodnictwo właściwe <math>\sigma\</math>, . | Uzupełnieniem czterech zasadniczych równań Maxwella są tzw. równania materiałowe, czyli związki między wektorami opisującymi pole elektryczne, pole magnetyczne oraz przepływ prądu elektrycznego. W równaniach tych pojawiają się parametry elektryczne i magnetyczne ośrodka: względna przenikalność elektryczna <math>\varepsilon_r\ </math>, i względna przenikalność magnetyczna <math>\mu_r\ </math>, oraz przewodnictwo właściwe <math>\sigma\ </math>, . | ||
Do opisu pola elektryczego i magnetycznego używane są cztery wektory <math>\overrightarrow{E}, \overrightarrow{D}, \overrightarrow{H}, \overrightarrow{B}\</math>, i ich strumienie. Zatem równania Maxwella można zapisać na różne sposoby. Odpowiedni dobór tych wielkosci fizycznych pozwala na taki zapis tych równań, który podkreśla ich podobieństwa i różnice oraz prostotę i piękno. Dotyczy to zarówno przedstawionych powyżej równań w postaci całkowej (która jest nieco bliższa doświadczeniu i naszej intuicji), jak również przedstawionej poniżej postaci różniczkowej tych równań (która jest nieco bardziej abstrakcyjna, ale ma również istotne zalety). | Do opisu pola elektryczego i magnetycznego używane są cztery wektory <math>\overrightarrow{E}, \overrightarrow{D}, \overrightarrow{H}, \overrightarrow{B}\ </math>, i ich strumienie. Zatem równania Maxwella można zapisać na różne sposoby. Odpowiedni dobór tych wielkosci fizycznych pozwala na taki zapis tych równań, który podkreśla ich podobieństwa i różnice oraz prostotę i piękno. Dotyczy to zarówno przedstawionych powyżej równań w postaci całkowej (która jest nieco bliższa doświadczeniu i naszej intuicji), jak również przedstawionej poniżej postaci różniczkowej tych równań (która jest nieco bardziej abstrakcyjna, ale ma również istotne zalety). | ||
Bardzo ważną konsekwencją równań Maxwella jest istnienie fali elektromagnetycznej, której równanie zostanie wyprowadzone z różniczkowej postaci tych równań w Wykładzie 15. | Bardzo ważną konsekwencją równań Maxwella jest istnienie fali elektromagnetycznej, której równanie zostanie wyprowadzone z różniczkowej postaci tych równań w Wykładzie 15. | ||
| Linia 263: | Linia 263: | ||
:iloczyn wektorowy operatora nabla i wektora | :iloczyn wektorowy operatora nabla i wektora | ||
*laplasjan <math>\Delta =\nabla \cdot \nabla=\frac{\partial^2}{\partial x^2}+ \frac{\partial^2}{\partial y^2}+ \frac{\partial^2}{\partial z^2} </math> | *laplasjan <math>\Delta =\nabla \cdot \nabla=\frac{\partial^2}{\partial x^2}+ \frac{\partial^2}{\partial y^2}+ \frac{\partial^2}{\partial z^2}</math> | ||
:iloczyn skalarny operatorów nabla | :iloczyn skalarny operatorów nabla | ||
| Linia 303: | Linia 303: | ||
'''Przykład 14.1''' | '''Przykład 14.1''' | ||
Przewodzący pręt o długości <math>l\</math>, wiruje z prędkością kątową <math>\overrightarrow{\omega}=[0, \omega, 0]</math> wokół osi OY prostopadłej do pręta i przechodzącej przez jego koniec, w stałym, jednorodnym polu magnetycznym o wektorze indukcji <math>\overrightarrow{B}=[0, 0, -B]</math> . | Przewodzący pręt o długości <math>l\ </math>, wiruje z prędkością kątową <math>\overrightarrow{\omega}=[0, \omega, 0]</math> wokół osi OY prostopadłej do pręta i przechodzącej przez jego koniec, w stałym, jednorodnym polu magnetycznym o wektorze indukcji <math>\overrightarrow{B}=[0, 0, -B]</math> . | ||
Obliczyć wartość napięcia między końcami pręta i określić jego polaryzację. | Obliczyć wartość napięcia między końcami pręta i określić jego polaryzację. | ||
Przyjąć, że <math>l = 1m</math>, <math>\omega = 50s^{-1}</math> , <math>B = 1T\</math>,. | Przyjąć, że <math>l = 1m</math>, <math>\omega = 50s^{-1}</math> , <math>B = 1T\ </math>,. | ||
Czy można tak dobrać wartość <math>\omega\</math>,, aby w układzie odniesienia związanym z prętem konkurencja między siłą bezwładności i siłą jaką na elektrony działa pole magnetyczne spowodowała, że napięcie między końcami pręta będzie równe zeru? | Czy można tak dobrać wartość <math>\omega\ </math>,, aby w układzie odniesienia związanym z prętem konkurencja między siłą bezwładności i siłą jaką na elektrony działa pole magnetyczne spowodowała, że napięcie między końcami pręta będzie równe zeru? | ||
| Linia 376: | Linia 376: | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | ||
W obwodzie zachodzą drgania wymuszone. Znając funkcję <math>q(t)\</math>, można wyznaczyć pozostałe funkcje opisujące stan fizyczny układu drgającego. | W obwodzie zachodzą drgania wymuszone. Znając funkcję <math>q(t)\ </math>, można wyznaczyć pozostałe funkcje opisujące stan fizyczny układu drgającego. | ||
'''Napięcie na kondensatorze''' | '''Napięcie na kondensatorze''' | ||
| Linia 384: | Linia 384: | ||
:<math>\begin{matrix}U_{C0}=U_0\frac{\omega_{0}^2}{\sqrt{(\omega_{0}^2-\omega^2)^2}+4\beta^2\omega^2}; &\varphi=arctg\frac{2\beta \omega}{\omega_{0}^2-\omega^2} \end{matrix}</math> | :<math>\begin{matrix}U_{C0}=U_0\frac{\omega_{0}^2}{\sqrt{(\omega_{0}^2-\omega^2)^2}+4\beta^2\omega^2}; &\varphi=arctg\frac{2\beta \omega}{\omega_{0}^2-\omega^2} \end{matrix}</math> | ||
Zależność amplitudy napięcia na kondensatorze od częstości wymuszania jest oczywiście taka sama jak amplitudy ładunku. Napięcie na kondensatorze jest zgodne w fazie z ładunkiem, a więc <math>\varphi\</math>, określa również jego przesunięcie fazowe względem napięcia wymuszającego. | Zależność amplitudy napięcia na kondensatorze od częstości wymuszania jest oczywiście taka sama jak amplitudy ładunku. Napięcie na kondensatorze jest zgodne w fazie z ładunkiem, a więc <math>\varphi\ </math>, określa również jego przesunięcie fazowe względem napięcia wymuszającego. | ||
W stanie rezonansu, czyli dla częstości wymuszania równej <math>\omega_r\</math>,, amplituda napięcia na kondensatorze osiąga wartość maksymalną: | W stanie rezonansu, czyli dla częstości wymuszania równej <math>\omega_r\ </math>,, amplituda napięcia na kondensatorze osiąga wartość maksymalną: | ||
:<math>\begin{matrix}(U_{C0})_{max}=\frac{(q_0)_{max}}{C}=U_0\frac{\omega_{0}^2}{2\beta \sqrt{\omega_{0}^2-\beta^2}} & dla & \omega_r=\sqrt{\omega_{0}^2-2\beta^2}; & \left(\beta <\omega_0 \frac{\sqrt{2}}{2}\right) \end{matrix}</math> | :<math>\begin{matrix}(U_{C0})_{max}=\frac{(q_0)_{max}}{C}=U_0\frac{\omega_{0}^2}{2\beta \sqrt{\omega_{0}^2-\beta^2}} & dla & \omega_r=\sqrt{\omega_{0}^2-2\beta^2}; & \left(\beta <\omega_0 \frac{\sqrt{2}}{2}\right) \end{matrix}</math> | ||
| Linia 394: | Linia 394: | ||
:<math>\varphi_r=arctg\frac{\sqrt{\omega_{0}^2-\beta^2}}{\beta}=arctg\frac{\omega_r}{\beta}</math> | :<math>\varphi_r=arctg\frac{\sqrt{\omega_{0}^2-\beta^2}}{\beta}=arctg\frac{\omega_r}{\beta}</math> | ||
Wartości graniczne: gdy częstość wymuszania dąży do zera, to amplituda napięcia na kondensatorze dąży do wartości <math>U_0\</math>, , zaś dla częstości znacznie większych od częstości własnej <math>\omega_0\</math>, dąży do zera. Przesunięcie fazowe zmienia się od zera dla bardzo małej częstości wymuszania do <math>\pi\</math>, dla częstości bardzo dużej. | Wartości graniczne: gdy częstość wymuszania dąży do zera, to amplituda napięcia na kondensatorze dąży do wartości <math>U_0\ </math>, , zaś dla częstości znacznie większych od częstości własnej <math>\omega_0\ </math>, dąży do zera. Przesunięcie fazowe zmienia się od zera dla bardzo małej częstości wymuszania do <math>\pi\ </math>, dla częstości bardzo dużej. | ||
'''Natężenie prądu''' | '''Natężenie prądu''' | ||
| Linia 402: | Linia 402: | ||
:<math>\begin{matrix}I_0=\frac{U_0}{L}\frac{\omega}{\sqrt{(\omega_{0}^2-\omega^2)^2}+4\beta^2\omega^2}; &\varphi_R=arctg\frac{\omega^2-\omega_{0}^2}{2\beta \omega} \end{matrix}</math> | :<math>\begin{matrix}I_0=\frac{U_0}{L}\frac{\omega}{\sqrt{(\omega_{0}^2-\omega^2)^2}+4\beta^2\omega^2}; &\varphi_R=arctg\frac{\omega^2-\omega_{0}^2}{2\beta \omega} \end{matrix}</math> | ||
Przedstawione wzory pokazują, że faza natężenia prądu różni się od fazy ładunku i napięcia na kondensatorze, a amplituda natężenia prądu jest inną funkcją częstości wymuszania. Badając funkcję <math>I_0(\omega)\</math>, możemy stwierdzić, że osiąga ona wartość maksymalną dla częstości wymuszania równej częstości własnej układu, niezależnie od wartości współczynnika tłumienia: | Przedstawione wzory pokazują, że faza natężenia prądu różni się od fazy ładunku i napięcia na kondensatorze, a amplituda natężenia prądu jest inną funkcją częstości wymuszania. Badając funkcję <math>I_0(\omega)\ </math>, możemy stwierdzić, że osiąga ona wartość maksymalną dla częstości wymuszania równej częstości własnej układu, niezależnie od wartości współczynnika tłumienia: | ||
:<math>\begin{matrix}(I_0)_{max}=\frac{U_0}{R} & i &\varphi_R=0 & dla & \omega=\omega_0 \end{matrix}</math> | :<math>\begin{matrix}(I_0)_{max}=\frac{U_0}{R} & i &\varphi_R=0 & dla & \omega=\omega_0 \end{matrix}</math> | ||
| Linia 432: | Linia 432: | ||
:<math>\varphi_L=arctg\left(-\frac{\sqrt{\omega_{0}^2-\beta^2}}{\beta}\right)-\pi=arctg\left(-\frac{\omega_r}{\beta}\right)-\pi</math> | :<math>\varphi_L=arctg\left(-\frac{\sqrt{\omega_{0}^2-\beta^2}}{\beta}\right)-\pi=arctg\left(-\frac{\omega_r}{\beta}\right)-\pi</math> | ||
Napięcie na zwojnicy ma fazę przeciwną względem napięcia na kondensatorze, zaś amplituda osiąga wartość największą dla częstości większej od częstości rezonansowej, a nawet większej od częstości własnej. Gdy współczynnik tłumienia zmienia się od zera do wartości granicznej to częstość ta rośnie od wartości <math>\omega_0\</math>, do nieskończoności. | Napięcie na zwojnicy ma fazę przeciwną względem napięcia na kondensatorze, zaś amplituda osiąga wartość największą dla częstości większej od częstości rezonansowej, a nawet większej od częstości własnej. Gdy współczynnik tłumienia zmienia się od zera do wartości granicznej to częstość ta rośnie od wartości <math>\omega_0\ </math>, do nieskończoności. | ||
</div></div> | </div></div> | ||
| Linia 440: | Linia 440: | ||
= Zadania = | = Zadania = | ||
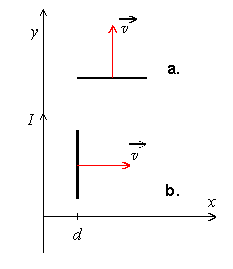
'''1.''' W polu magnetycznym wytworzonym wokół bardzo długiego, cienkiego przewodu prostoliniowego, w którym płynie prąd o natężeniu <math>I\</math>,, porusza się ze stałą prędkością <math>\overrightarrow{v}\</math>, metalowy pręt o długości <math>l\</math>,. Prędkość jest prostopadła do pręta. Obliczyć stosunek wartości napięcia między końcami pręta dla dwóch sposobów przesuwania pręta: | '''1.''' W polu magnetycznym wytworzonym wokół bardzo długiego, cienkiego przewodu prostoliniowego, w którym płynie prąd o natężeniu <math>I\ </math>,, porusza się ze stałą prędkością <math>\overrightarrow{v}\ </math>, metalowy pręt o długości <math>l\ </math>,. Prędkość jest prostopadła do pręta. Obliczyć stosunek wartości napięcia między końcami pręta dla dwóch sposobów przesuwania pręta: | ||
:'''a.''' wektor <math>\overrightarrow{v}\</math>, jest równoległy do przewodu | :'''a.''' wektor <math>\overrightarrow{v}\ </math>, jest równoległy do przewodu | ||
:'''b.''' wektor <math>\overrightarrow{v}\</math>, jest prostopadły do przewodu | :'''b.''' wektor <math>\overrightarrow{v}\ </math>, jest prostopadły do przewodu | ||
:[[Grafika:PF_M14_Zad_Rys1.png]] | :[[Grafika:PF_M14_Zad_Rys1.png]] | ||
| Linia 458: | Linia 458: | ||
W pierwszym przypadku napięcie ma stałą wartość (pręt porusza się tak, że średnia wartość wektora indukcji magnetycznej jest stała), natomiast w drugim przypadku napięcie maleje w miarę oddalania się od długiego przewodu(pręt przemieszcza się w obszary coraz słabszego pola). Zatem stosunek napięć jest zależny od czasu. | W pierwszym przypadku napięcie ma stałą wartość (pręt porusza się tak, że średnia wartość wektora indukcji magnetycznej jest stała), natomiast w drugim przypadku napięcie maleje w miarę oddalania się od długiego przewodu(pręt przemieszcza się w obszary coraz słabszego pola). Zatem stosunek napięć jest zależny od czasu. | ||
:<math>\frac{U_1}{U_2}=\frac{d+vt}{l}ln\left(1+\frac{l}{d}\right) </math> | :<math>\frac{U_1}{U_2}=\frac{d+vt}{l}ln\left(1+\frac{l}{d}\right)</math> | ||
</div></div> | </div></div> | ||
| Linia 464: | Linia 464: | ||
<hr width="100%"> | <hr width="100%"> | ||
'''2.''' W odległości <math>a\</math>, od nieskończenie długiego przewodu prostoliniowego w którym płynie prąd o natężeniu <math>I\</math>, umieszczono kwadratowy obwód o boku <math>a\</math>, i oporności <math>R\</math>,. Obliczyć: | '''2.''' W odległości <math>a\ </math>, od nieskończenie długiego przewodu prostoliniowego w którym płynie prąd o natężeniu <math>I\ </math>, umieszczono kwadratowy obwód o boku <math>a\ </math>, i oporności <math>R\ </math>,. Obliczyć: | ||
:'''a.''' Strumień pola magnetycznego przez powierzchnię obwodu. | :'''a.''' Strumień pola magnetycznego przez powierzchnię obwodu. | ||
:'''b.''' Ładunek jaki przepłynie w obwodzie po wyłączeniu prądu <math>I\</math>,. | :'''b.''' Ładunek jaki przepłynie w obwodzie po wyłączeniu prądu <math>I\ </math>,. | ||
:'''c.''' Energię przekazaną do obwodu, przy założeniu, że zanik prądu <math>I\</math>, ma charakter eksponencjalny, z czasem relaksacji <math>\tau\</math>,. | :'''c.''' Energię przekazaną do obwodu, przy założeniu, że zanik prądu <math>I\ </math>, ma charakter eksponencjalny, z czasem relaksacji <math>\tau\ </math>,. | ||
| Linia 487: | Linia 487: | ||
<hr width="100%"> | <hr width="100%"> | ||
'''3.''' Na długich poziomych szynach spiętych opornikiem o oporności <math>R\</math>, leży pręt o masie <math>m\</math>, i długości <math>l\</math>,. Wektor indukcji <math>\overrightarrow{B}\</math>, stałego, jednorodnego pola magnetycznego jest skierowany przeciwnie do wektora natężenia pola grawitacyjnego <math>\overrightarrow{g}\</math>, . Obliczyć moc potrzebną do przesuwania pręta ze stałą prędkością <math>\overrightarrow{v}\</math>, . Zaniedbać oporność szyn i pręta oraz tarcie pręta o szyny. | '''3.''' Na długich poziomych szynach spiętych opornikiem o oporności <math>R\ </math>, leży pręt o masie <math>m\ </math>, i długości <math>l\ </math>,. Wektor indukcji <math>\overrightarrow{B}\ </math>, stałego, jednorodnego pola magnetycznego jest skierowany przeciwnie do wektora natężenia pola grawitacyjnego <math>\overrightarrow{g}\ </math>, . Obliczyć moc potrzebną do przesuwania pręta ze stałą prędkością <math>\overrightarrow{v}\ </math>, . Zaniedbać oporność szyn i pręta oraz tarcie pręta o szyny. | ||
Aktualna wersja na dzień 12:03, 5 wrz 2023
Wykład
 |
Materiały do ćwiczeń
Drgania harmoniczne
Indukcja elektromagnetyczna
Przykład 14.1
Przewodzący pręt o długości , wiruje z prędkością kątową wokół osi OY prostopadłej do pręta i przechodzącej przez jego koniec, w stałym, jednorodnym polu magnetycznym o wektorze indukcji .
Obliczyć wartość napięcia między końcami pręta i określić jego polaryzację.
Przyjąć, że , , ,.
Czy można tak dobrać wartość ,, aby w układzie odniesienia związanym z prętem konkurencja między siłą bezwładności i siłą jaką na elektrony działa pole magnetyczne spowodowała, że napięcie między końcami pręta będzie równe zeru?
Drgania elektromagnetyczne
Przykład 14.2
Do obwodu o oporze R, indukcyjności L i pojemności C dołączono źródło napięcia . Znaleźć zależność od czasu napięcia na kondensatorze, natężenia prądu, napięcia na oporniku oraz napięcia na zwojnicy.
Zadania
1. W polu magnetycznym wytworzonym wokół bardzo długiego, cienkiego przewodu prostoliniowego, w którym płynie prąd o natężeniu ,, porusza się ze stałą prędkością , metalowy pręt o długości ,. Prędkość jest prostopadła do pręta. Obliczyć stosunek wartości napięcia między końcami pręta dla dwóch sposobów przesuwania pręta:
- a. wektor , jest równoległy do przewodu
- b. wektor , jest prostopadły do przewodu
Skomentować otrzymany wynik.
2. W odległości , od nieskończenie długiego przewodu prostoliniowego w którym płynie prąd o natężeniu , umieszczono kwadratowy obwód o boku , i oporności ,. Obliczyć:
- a. Strumień pola magnetycznego przez powierzchnię obwodu.
- b. Ładunek jaki przepłynie w obwodzie po wyłączeniu prądu ,.
- c. Energię przekazaną do obwodu, przy założeniu, że zanik prądu , ma charakter eksponencjalny, z czasem relaksacji ,.
3. Na długich poziomych szynach spiętych opornikiem o oporności , leży pręt o masie , i długości ,. Wektor indukcji , stałego, jednorodnego pola magnetycznego jest skierowany przeciwnie do wektora natężenia pola grawitacyjnego , . Obliczyć moc potrzebną do przesuwania pręta ze stałą prędkością , . Zaniedbać oporność szyn i pręta oraz tarcie pręta o szyny.
4. W obwodzie RLC zachodzą elektromagnetyczne drgania wymuszone pod wpływem napięcia . Obliczyć średnią moc pochłanianą przez obwód w ciągu jednego okresu drgań. Dla jakiej wartości częstości wymuszania wartość tej mocy jest największa?