PEE Moduł 6: Różnice pomiędzy wersjami
Nie podano opisu zmian |
m Zastępowanie tekstu – „\</math>” na „\ </math>” |
||
| (Nie pokazano 20 wersji utworzonych przez 3 użytkowników) | |||
| Linia 1: | Linia 1: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M6_Slajd1.png]] | |valign="top" width="500px"|[[Grafika:PEE_M6_Slajd1.png|500px]] | ||
|valign="top"| | |valign="top"| | ||
|} | |} | ||
| Linia 7: | Linia 7: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M6_Slajd2.png]] | |valign="top" width="500px"|[[Grafika:PEE_M6_Slajd2.png|500px]] | ||
|valign="top"| | |valign="top"|'''Definicja układu trójfazowego''' | ||
'''Definicja układu trójfazowego''' | |||
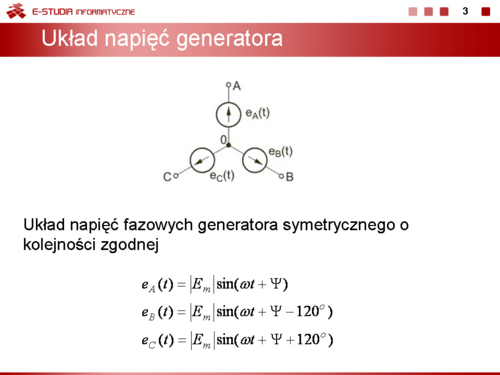
Układem trójfazowym nazywamy układ trzech obwodów elektrycznych, w których istnieją trzy źródła napięć sinusoidalnych o jednakowej częstotliwości, przesunięte względem siebie o określony kąt fazowy i wytworzone w jednym generatorze zwanym generatorem trójfazowym. Poszczególne obwody generatora trójfazowego nazywać będziemy '''fazami''' i oznaczać literami A, B, C lub kolejnymi cyframi 1, 2, 3. | Układem trójfazowym nazywamy układ trzech obwodów elektrycznych, w których istnieją trzy źródła napięć sinusoidalnych o jednakowej częstotliwości, przesunięte względem siebie o określony kąt fazowy i wytworzone w jednym generatorze zwanym generatorem trójfazowym. Poszczególne obwody generatora trójfazowego nazywać będziemy '''fazami''' i oznaczać literami A, B, C lub kolejnymi cyframi 1, 2, 3. | ||
| Linia 18: | Linia 16: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M6_Slajd3.png]] | |valign="top" width="500px"|[[Grafika:PEE_M6_Slajd3.png|500px]] | ||
|valign="top"|Przykład połączenia 3 faz generatora w jeden układ gwiazdowy przedstawiony jest na rysunku obok (slajd 3). | |valign="top"|Przykład połączenia 3 faz generatora w jeden układ gwiazdowy przedstawiony jest na rysunku obok (slajd 3). | ||
| Linia 24: | Linia 22: | ||
: <math>e_A(t)=|E_m|sin(\omega t+\Psi)</math> | : <math>e_A(t)=|E_m|sin(\omega t+\Psi)</math> | ||
: <math>e_B(t)=|E_m|sin(\omega t+\Psi-120^\circ)</math> | : <math>e_B(t)=|E_m|sin(\omega t+\Psi-120^\circ)</math> | ||
: <math>e_C(t)=|E_m|sin(\omega t+\Psi+120^\circ)</math> | : <math>e_C(t)=|E_m|sin(\omega t+\Psi+120^\circ)</math> | ||
| Linia 33: | Linia 33: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M6_Slajd4.png]] | |valign="top" width="500px"|[[Grafika:PEE_M6_Slajd4.png|500px]] | ||
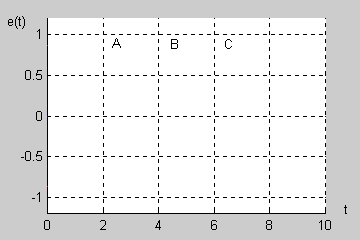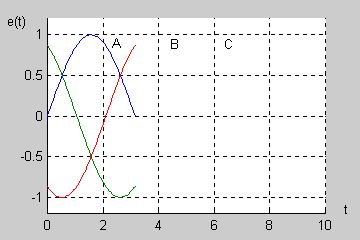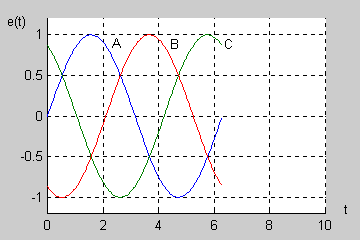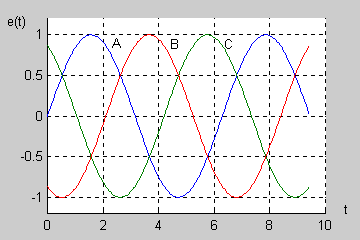
|valign="top"|W normalnym systemie trójfazowym przyjmuje się tzw. '''kolejność wirowania zgodną''', w której faza B opóźnia się względem fazy A o kąt <math>120^\circ</math> a faza C (opóźniona względem fazy B o kolejny kąt <math>120^\circ</math> ) wyprzedza fazę A o kąt równy <math>120^\circ</math>. | |valign="top"|W normalnym systemie trójfazowym przyjmuje się tzw. '''kolejność wirowania zgodną''', w której faza B opóźnia się względem fazy A o kąt <math>120^\circ</math> a faza C (opóźniona względem fazy B o kolejny kąt <math>120^\circ</math> ) wyprzedza fazę A o kąt równy <math>120^\circ</math>. | ||
Na rysunku obok (slajd 4) i poniżej przedstawiono przebiegi czasowe napięć trójfazowych przy kącie początkowym <math>\Psi</math> równym zeru. Napięcia są zmienne sinusoidalnie przy czym występują regularne przesunięcia o kąt <math>120^\circ</math> między poszczególnymi sinusoidami. | Na rysunku obok (slajd 4) i na aminacji poniżej przedstawiono przebiegi czasowe napięć trójfazowych przy kącie początkowym <math>\Psi\ </math>, równym zeru. Napięcia są zmienne sinusoidalnie przy czym występują regularne przesunięcia o kąt <math>120^\circ</math> między poszczególnymi sinusoidami. | ||
[[Grafika:PEE_M6_anim_1.gif]] | [[Grafika:PEE_M6_anim_1.gif]] | ||
| Linia 45: | Linia 46: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M6_Slajd5.png]] | |valign="top" width="500px"|[[Grafika:PEE_M6_Slajd5.png|500px]] | ||
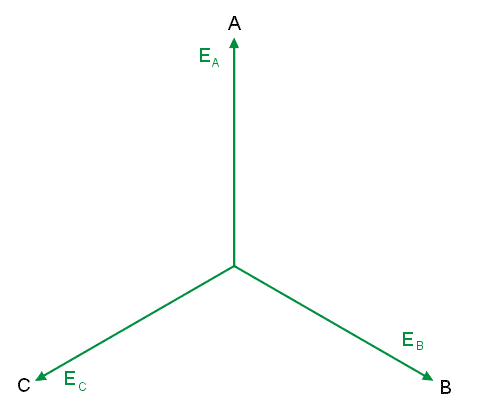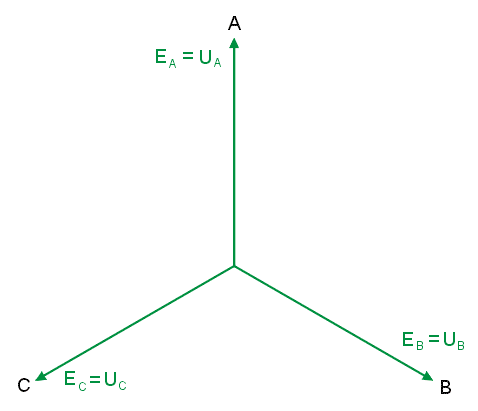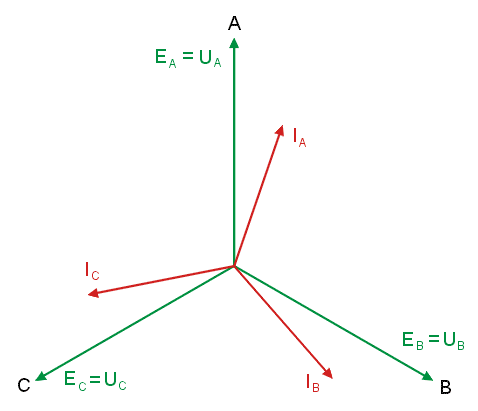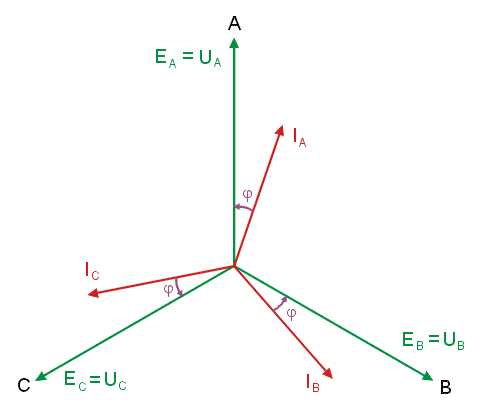
|valign="top"|'''Układ napięć fazowych''' | |valign="top"|'''Układ napięć fazowych''' | ||
| Linia 51: | Linia 52: | ||
: <math>E_A={|E_m| \over \sqrt{2}}e^{j\Psi}</math> | : <math>E_A={|E_m| \over \sqrt{2}}e^{j\Psi}</math> | ||
: <math>E_B={|E_m| \over \sqrt{2}}e^{j\Psi-120^\circ}=E_Ae^{-j120^\circ}</math> | |||
: <math>E_A={|E_m| \over \sqrt{2}}e^{j\Psi+120^\circ}=E_Ae^{j120^\circ}</math> | : <math>E_B={|E_m| \over \sqrt{2}}e^{j(\Psi-120^\circ)}=E_Ae^{-j120^\circ}</math> | ||
: <math>E_A={|E_m| \over \sqrt{2}}e^{j(\Psi+120^\circ)}=E_Ae^{j120^\circ}</math> | |||
W praktyce wobec nieustannej zmiany wartości napięć w czasie faza początkowa <math>\Psi</math> może być przyjęta dowolnie. Najczęściej dla wygody zakładać będziemy, że jest równa zeru. Wykres wektorowy napięć trójfazowych opisanych powyższymi zależnościami dla kąta fazowego <math>\Psi \neq 0</math> przedstawiony jest na rysunku obok (slajd 5). | W praktyce wobec nieustannej zmiany wartości napięć w czasie faza początkowa <math>\Psi</math> może być przyjęta dowolnie. Najczęściej dla wygody zakładać będziemy, że jest równa zeru. Wykres wektorowy napięć trójfazowych opisanych powyższymi zależnościami dla kąta fazowego <math>\Psi \neq 0</math> przedstawiony jest na rysunku obok (slajd 5). | ||
| Linia 62: | Linia 65: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M6_Slajd6.png]] | |valign="top" width="500px"|[[Grafika:PEE_M6_Slajd6.png|500px]] | ||
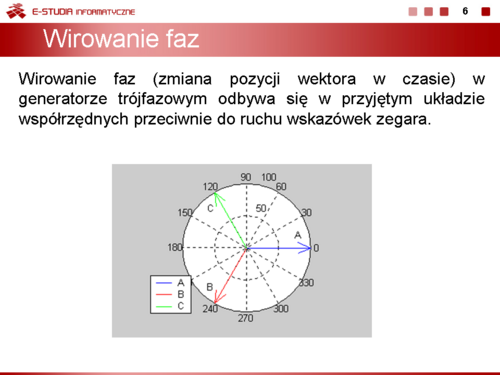
|valign="top"|Wirowanie faz (zmiana pozycji wektora w czasie) w generatorze trójfazowym odbywa się w przyjętym układzie współrzędnych przeciwnie do ruchu wskazówek zegara. | |valign="top"|Wirowanie faz (zmiana pozycji wektora w czasie) w generatorze trójfazowym odbywa się w przyjętym układzie współrzędnych przeciwnie do ruchu wskazówek zegara. | ||
[[Grafika:PEE_M6_anim_2.gif]] | [[Grafika:PEE_M6_anim_2.gif]] | ||
Rysunek powyżej pokazuje wektory napięć generatora trójfazowego wirujące w czasie. Wektory fazy B i C nadążają za wektorem A, przy czym przesunięcia fazowe między nimi są stałe i równe dokładnie <math>120^\circ</math>. Ważną cechą trójfazowego generatora symetrycznego jest zerowanie się sumy napięć fazowych | Rysunek powyżej pokazuje wektory napięć generatora trójfazowego wirujące w czasie. Wektory fazy B i C nadążają za wektorem A, przy czym przesunięcia fazowe między nimi są stałe i równe dokładnie <math>120^\circ</math>. Ważną cechą trójfazowego generatora symetrycznego jest zerowanie się sumy napięć fazowych | ||
| Linia 74: | Linia 79: | ||
: <math>E_A+E_B+E_C=E_A+E_Ae^{-j120^\circ}+E_Ae^{j120^\circ}=</math> | : <math>E_A+E_B+E_C=E_A+E_Ae^{-j120^\circ}+E_Ae^{j120^\circ}=</math> | ||
: <math> | : <math>E_A \left ( 1-0,5-j{\sqrt{3} \over 2}-0,5+j{\sqrt{3} \over 2} \right )=0</math> | ||
|} | |} | ||
| Linia 80: | Linia 85: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M6_Slajd7.png]] | |valign="top" width="500px"|[[Grafika:PEE_M6_Slajd7.png|500px]] | ||
|valign="top"|'''Układ napięć międzyfazowych''' | |valign="top"|'''Układ napięć międzyfazowych''' | ||
| Linia 86: | Linia 91: | ||
: <math>E_{AB}=E_A-E_B</math> | : <math>E_{AB}=E_A-E_B</math> | ||
: <math>E_{BC}=E_B-E_C</math> | : <math>E_{BC}=E_B-E_C</math> | ||
: <math>E_{CA}=E_C-E_A</math> | : <math>E_{CA}=E_C-E_A</math> | ||
Z definicji napięć międzyfazowych wynika, że niezależnie od symetrii ich suma jest zawsze równa zeru gdyż wszystkie napięcia tworzą trójkąt zamknięty. Rysunek na sladzie nr 7 pokazuje układ napięć międzyfazowych generatora trójfazowego z przyjętymi oznaczeniami. Symbol <math>E_{AB}</math> oznacza, że strzałka wektora napięcia na wykresie jest skierowana w stronę pierwszego wskaźnika w oznaczeniu (u nas litera A). | Z definicji napięć międzyfazowych wynika, że niezależnie od symetrii ich suma jest zawsze równa zeru gdyż wszystkie napięcia tworzą trójkąt zamknięty. Rysunek na sladzie nr 7 pokazuje układ napięć międzyfazowych generatora trójfazowego z przyjętymi oznaczeniami. Symbol <math>E_{AB}\ </math>, oznacza, że strzałka wektora napięcia na wykresie jest skierowana w stronę pierwszego wskaźnika w oznaczeniu (u nas litera A). Z symetrii napięć fazowych wynika bezpośrednio symetria napięć międzyfazowych. Napięcia te są równe i przesunięte względem siebie o kąt <math>120^\circ</math>, czyli | ||
: <math>E_{AB}=E_A-E_B</math> | |||
: <math>E_{BC}=E_{AB}e^{-j120^\circ}</math> | : <math>E_{BC}=E_{AB}e^{-j120^\circ}</math> | ||
: <math>E_{CA}=E_{AB}e^{j120^\circ}</math> | : <math>E_{CA}=E_{AB}e^{j120^\circ}</math> | ||
Układ napięć międzyfazowych symetrycznych tworzy więc trójkąt równoboczny. Wykorzystując relacje obowiązujące dla tego trójkąta łatwo jest udowodnić, że napięcie międzyfazowe jest <math>\sqrt{3}</math> razy większe niż napięcie fazowe, co zapiszemy w ogólności jako | Układ napięć międzyfazowych symetrycznych tworzy więc trójkąt równoboczny. Wykorzystując relacje obowiązujące dla tego trójkąta łatwo jest udowodnić, że napięcie międzyfazowe jest <math>\sqrt{3}\ </math>, razy większe niż napięcie fazowe, co zapiszemy w ogólności jako | ||
: <math>|E_{mf}|=\sqrt{3}|E_f|</math> | : <math>|E_{mf}|=\sqrt{3}|E_f|</math> | ||
| Linia 107: | Linia 114: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M6_Slajd8.png]] | |valign="top" width="500px"|[[Grafika:PEE_M6_Slajd8.png|500px]] | ||
|valign="top"| | |valign="top"|'''Połączenia trójfazowe generatora i odbiornika''' | ||
'''Połączenia trójfazowe generatora i odbiornika''' | |||
Układ napięć fazowych generatora może być połączony bądź w gwiazdę bądź w trójkąt. Schemat obu połączeń przedstawiony jest na rysunku obok (slajd nr 8). | Układ napięć fazowych generatora może być połączony bądź w gwiazdę bądź w trójkąt. Schemat obu połączeń przedstawiony jest na rysunku obok (slajd nr 8). | ||
| Linia 120: | Linia 125: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M6_Slajd9.png]] | |valign="top" width="500px"|[[Grafika:PEE_M6_Slajd9.png|500px]] | ||
|valign="top"|W układzie trójfazowym odbiornik zawiera również trzy fazy, przy czym może być on połączony w gwiazdę lub w trójkąt. Oba sposoby połączenia odbiornika przedstawione są na rysunku na slajdzie nr 8. | |valign="top"|W układzie trójfazowym odbiornik zawiera również trzy fazy, przy czym może być on połączony w gwiazdę lub w trójkąt. Oba sposoby połączenia odbiornika przedstawione są na dolnym rysunku na slajdzie nr 8. | ||
W zależności od sposobu połączenia generatora i odbiornika można w układach trójfazowych wyróżnić cztery rodzaje połączeń. Są to: | W zależności od sposobu połączenia generatora i odbiornika można w układach trójfazowych wyróżnić cztery rodzaje połączeń. Są to: | ||
| Linia 135: | Linia 140: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M6_Slajd10.png]] | |valign="top" width="500px"|[[Grafika:PEE_M6_Slajd10.png|500px]] | ||
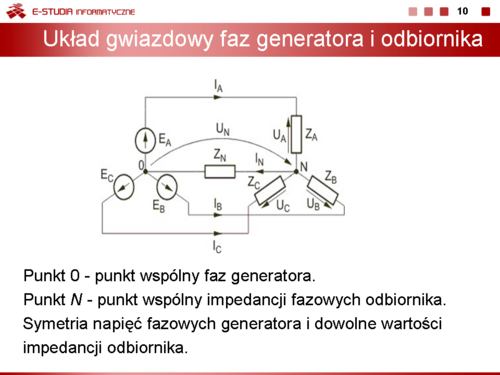
|valign="top"|'''Układ gwiazdowy faz generatora i odbiornika''' | |valign="top"|'''Układ gwiazdowy faz generatora i odbiornika''' | ||
Rozpatrzmy układ połączeń gwiazdowych odbiornika i generatora (gwiazda-gwiazda) z oznaczeniami prądów i napięć przedstawionymi na rysunku obok (slajd nr 10). | Rozpatrzmy układ połączeń gwiazdowych odbiornika i generatora (gwiazda-gwiazda) z oznaczeniami prądów i napięć przedstawionymi na rysunku obok (slajd nr 10). | ||
Punkt 0 oznacza punkt wspólny faz generatora. Punkt <math>N\ | Punkt 0 oznacza punkt wspólny faz generatora. Punkt <math>N\ </math>, jest punktem wspólnym impedancji fazowych odbiornika. Zakładamy symetrię napięć fazowych generatora i dowolne wartości impedancji odbiornika. Przyjmijmy do analizy układ czteroprzewodowy z impedancją przewodu zerowego równa <math>Z_N</math>. Wartość impedancji <math>Z_N</math> może być dowolna, w szczególności zerowa (bezpośrednie zwarcie punktów wspólnych generatora i odbiornika) lub nieskończona (układ trójprzewodowy bez przewodu zerowego). Napięcie między punktem zerowym odbiornika i generatora oznaczymy przez <math>U_N</math> i nazywać będziemy '''napięciem niezrównoważenia'''. | ||
|} | |} | ||
| Linia 146: | Linia 151: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M6_Slajd11.png]] | |valign="top" width="500px"|[[Grafika:PEE_M6_Slajd11.png|500px]] | ||
|valign="top"|Układ napięć trójfazowych odbiornika tworzą napięcia na poszczególnych jego fazach, czyli <math>U_A</math>, <math>U_B</math>, <math>U_C</math>. W efekcie w obwodzie trójfazowym o połączeniu gwiazda-gwiazda wyróżnia się dwa układy napięć trójfazowych gwiazdowych: generatora <math>E_A</math>, <math>E_B</math>, <math>E_C</math> i odbiornika <math>U_A</math>, <math>U_B</math>, <math>U_C</math>. | |valign="top"|Układ napięć trójfazowych odbiornika tworzą napięcia na poszczególnych jego fazach, czyli <math>U_A</math>, <math>U_B</math>, <math>U_C</math>. W efekcie w obwodzie trójfazowym o połączeniu gwiazda-gwiazda wyróżnia się dwa układy napięć trójfazowych gwiazdowych: generatora <math>E_A</math>, <math>E_B</math>, <math>E_C</math> i odbiornika <math>U_A</math>, <math>U_B</math>, <math>U_C</math>. | ||
| Linia 157: | Linia 162: | ||
: <math>U_N={E_AY_A+E_BY_B+E_CY_C \over (Y_A+Y_B+Y_C+Y_N)}</math> | : <math>U_N={E_AY_A+E_BY_B+E_CY_C \over (Y_A+Y_B+Y_C+Y_N)}</math> | ||
gdzie wielkości oznaczone symbolem <math>Y\ | gdzie wielkości oznaczone symbolem <math>Y\ </math>, są admitancjami: <math>Y_A={1 \over Z_A}</math>, <math>Y_B={1 \over Z_B}</math>, <math>Y_C={1 \over Z_C}</math> oraz <math>Y_N={1 \over Z_N}</math>. Wyznaczenie wartości napięcia <math>U_N</math> pozwala obliczyć wartości napięć odbiornikowych. Z prawa napięciowego Kirchhoffa napisanego dla trzech oczek w obwodzie wynika | ||
: <math>U_A=E_A-U_N</math> | : <math>U_A=E_A-U_N</math> | ||
: <math>U_B=E_B-U_N</math> | : <math>U_B=E_B-U_N</math> | ||
: <math>U_C=E_C-U_N</math> | : <math>U_C=E_C-U_N</math> | ||
|} | |||
Przy znanych wartościach admitancji odbiornika obliczenie prądu polega na zastosowaniu prawa Ohma. Mianowicie | <hr width="100%"> | ||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:PEE_M6_Slajd11a.png|500px]] | |||
|valign="top"|Przy znanych wartościach admitancji odbiornika obliczenie prądu polega na zastosowaniu prawa Ohma. Mianowicie | |||
: <math>I_A=Y_AU_A</math> | : <math>I_A=Y_AU_A</math> | ||
: <math>I_B=Y_BU_B</math> | : <math>I_B=Y_BU_B</math> | ||
: <math>I_C=Y_CU_C</math> | : <math>I_C=Y_CU_C</math> | ||
: <math>I_N=Y_NU_N</math> | : <math>I_N=Y_NU_N</math> | ||
Suma prądów w węźle <math>N\ | Suma prądów w węźle <math>N\ </math>, jest równa zeru, zatem <math>I_A+I_B+I_C=I_N</math>. Moce wydzielone w odbiorniku trójfazowym oblicza się jako sumę mocy wydzielonych w poszczególnych fazach odbiornika, czyli | ||
: <math>S_A=P_A+jQ_A=U_AI_A^*</math> | : <math>S_A=P_A+jQ_A=U_AI_A^*</math> | ||
: <math>S_B=P_B+jQ_B=U_BI_B^*</math> | : <math>S_B=P_B+jQ_B=U_BI_B^*</math> | ||
: <math>S_C=P_C+jQ_C=U_CI_C^*</math> | : <math>S_C=P_C+jQ_C=U_CI_C^*</math> | ||
| Linia 179: | Linia 196: | ||
: <math>S_N=P_N+jQ_N=U_NI_N^*</math> | : <math>S_N=P_N+jQ_N=U_NI_N^*</math> | ||
|} | |} | ||
| Linia 185: | Linia 201: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M6_Slajd12.png]] | |valign="top" width="500px"|[[Grafika:PEE_M6_Slajd12.png|500px]] | ||
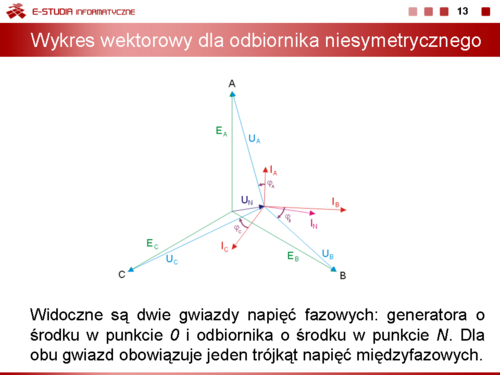
|valign="top"|Otrzymane wyniki można zinterpretować na wykresie wektorowym prądów i napięć w obwodzie. Rysunek | |valign="top"|Otrzymane wyniki można zinterpretować na wykresie wektorowym prądów i napięć w obwodzie. | ||
Rysunek na slajdzie obok przedstawia wykres wektorowy prądów i napięć dla przypadku obciążenia niesymetrycznego. Animacja poniżej przedstawia sposób konstrukcji wykresu wektorowego. | |||
[[Grafika:PEE_M6_anim_3.gif]] | [[Grafika:PEE_M6_anim_3.gif]] | ||
Widoczne są dwie gwiazdy napięć fazowych: generatora o środku w punkcie <math>0\ | Widoczne są dwie gwiazdy napięć fazowych: generatora o środku w punkcie <math>0\ </math>, i odbiornika o środku w punkcie <math>N\ </math>,. Dla obu gwiazd obowiązuje jeden trójkąt napięć międzyfazowych. Przesunięcie potencjału punktu <math>N\ </math>, względem <math>0\ </math>, (napięcie <math>U_N</math> różne od zera) jest spowodowane niesymetrią odbiornika. | ||
|} | |} | ||
| Linia 197: | Linia 214: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M6_Slajd13.png]] | |valign="top" width="500px"|[[Grafika:PEE_M6_Slajd13.png|500px]] | ||
|valign="top"|W pracy układu trójfazowego gwiazdowego można wyróżnić kilka szczególnych przypadków. | |valign="top"|W pracy układu trójfazowego gwiazdowego można wyróżnić kilka szczególnych przypadków. | ||
* '''Odbiornik symetryczny''' (<math>Z_A=Z_B=Z_C=Z</math>) z dowolną wartością impedancji przewodu zerowego | * '''Odbiornik symetryczny''' (<math>Z_A=Z_B=Z_C=Z</math>) z dowolną wartością impedancji przewodu zerowego | ||
W tym przypadku napięcie niezrównoważenia jest równe zeru a anpięcia fazowe odbiornika są równe napięciom fazowym generatora. Prądy w takim przypadku oblicza się ze wzorów podanych na slajdzie obok. Prąd przewodu zerowego <math>I_N=0</math>. Wszystkie prądy fazowe są równe co do amplitydy i przesunięte w fazie o <math>120^\circ</math>. | |||
|} | |} | ||
| Linia 207: | Linia 225: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M6_Slajd14.png]] | |valign="top" width="500px"|[[Grafika:PEE_M6_Slajd14.png|500px]] | ||
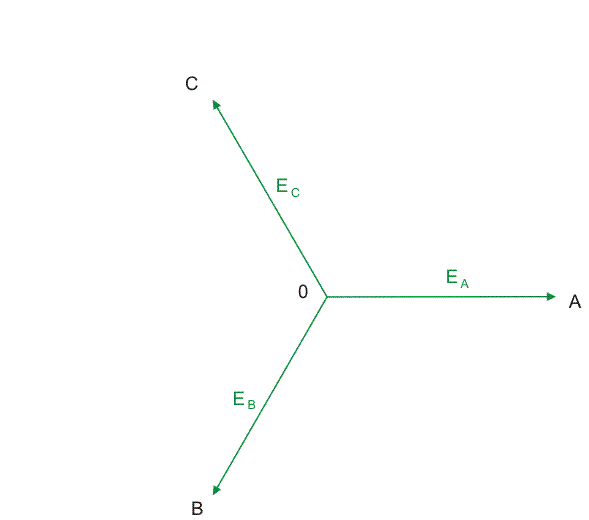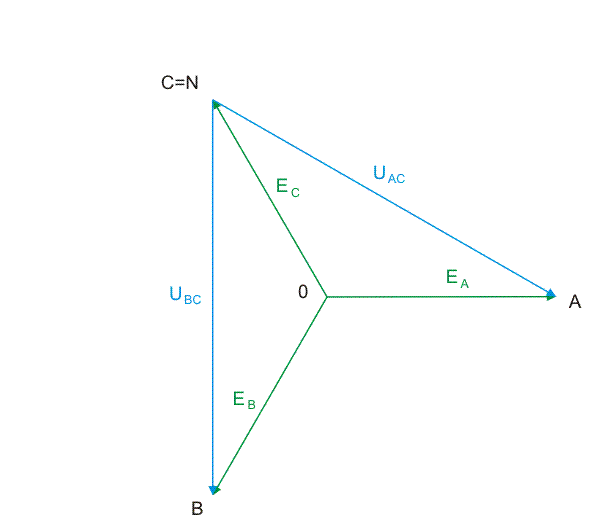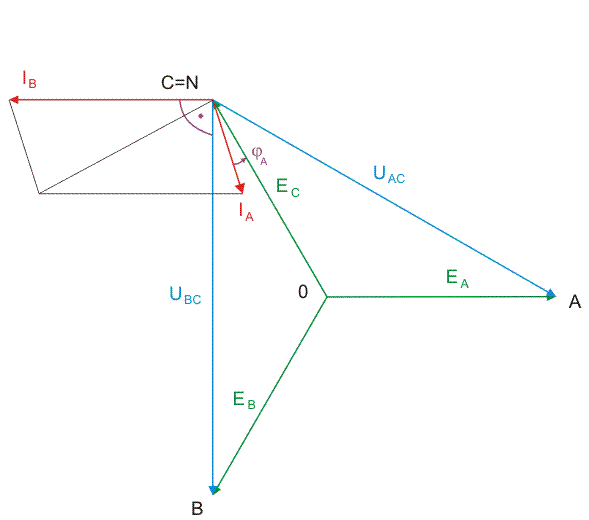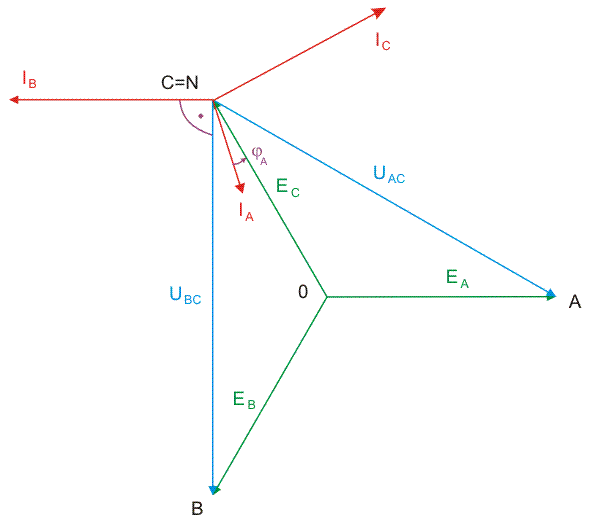
|valign="top"| | |valign="top"|Rysunek na slajdzie obok przedstawia wykres wektorowy prądów i napięć dla tego przypadku. Animacja poniżej przedstawia sposób konstrukcji wykresu wektorowego. | ||
[[Grafika:PEE_M6_anim_4.gif]] | [[Grafika:PEE_M6_anim_4.gif]] | ||
| Linia 218: | Linia 236: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M6_Slajd15.png]] | |valign="top" width="500px"|[[Grafika:PEE_M6_Slajd15.png|500px]] | ||
|valign="top"|* Odbiornik niesymetryczny przy zwartym przewodzie zerowym | |valign="top"| | ||
*'''Odbiornik niesymetryczny przy zwartym przewodzie zerowym''' | |||
W tym przypadku napięcie niezrównoważenia <math>U_N=0</math>, a prąd przewodu zerowego w ogólnym przypadku <math>I_N \neq 0</math>. Prądy fazowe są wówczas określane bezpośrednio na podstawie układu napięć generatorowych. Suma tych prądów w ogólnym przypadku odbiornika niesymetrycznego jest różna od zera | |||
: <math>I_N = I_A+I_B+I_C</math> | |||
Wykres wektorowy prądów i napięć w układzie trójfazowym niesymetrycznym przy zwarciu bezimpedancyjnym punktów wspólnych odbiornika i generatora przedstawiony jest na rysunku poniżej oraz na slajdzie obok. | |||
[[Grafika:PEE_M6_anim_5.gif]] | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:PEE_M6_Slajd16.png|500px]] | |||
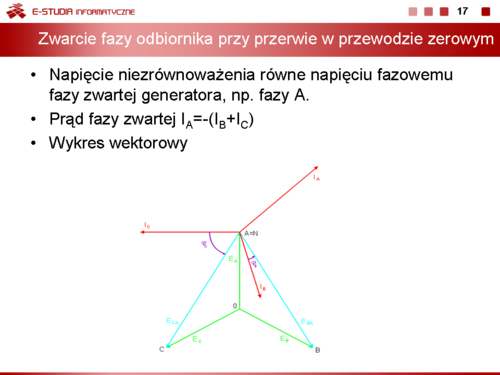
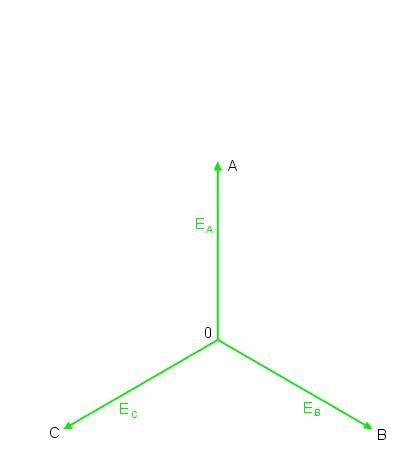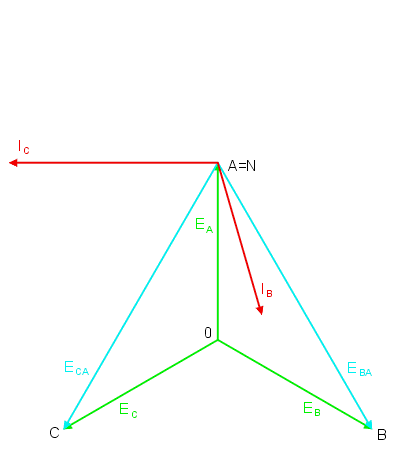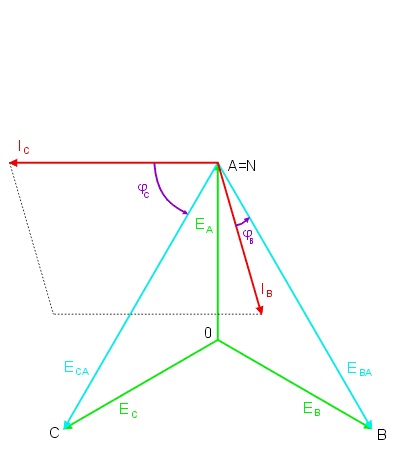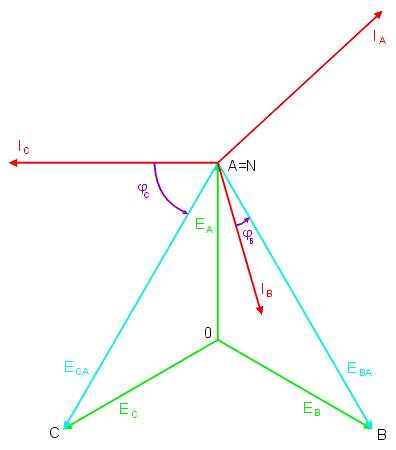
|valign="top"|*'''Zwarcie fazy odbiornika przy przerwie w przewodzie zerowym''' | |||
W tym przypadku napięcie niezrównoważenia jest równe napięciu fazowemu fazy zwartej. | |||
Prąd fazy zwartej nie może być określony z prawa Ohma, gdyż zarówno napięcie na fazie odbiornika jak i jego impedancja są równe zeru. Okresla sie go z prawa prądowego Kirchhoffa, zgodnie z którym | |||
: <math>I_A=-I_B-I_C</math> | |||
Wykres wektorowy prądów i napięć w układzie trójfazowym dla przypadku zwarcia fazy A odbiornika przedstawiony jest na rysunku poniżej oraz na slajdzie obok. | |||
[[Grafika:PEE_M6_anim_6.gif]] | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:PEE_M6_Slajd17.png|500px]] | |||
|valign="top"|Jako przykład obliczymy prądy i napięcia poszczególnych faz odbiornika w układzie przedstawionym na rysunku obok. Przyjmiemy zasilanie trójfazowe symetryczne o napięciu fazowym równym <math>400V</math>. Wartości parametrów obwodu są następujące: <math>R=40\Omega</math>, <math>X_C=30\Omega</math>, <math>X_L=60\Omega</math>, <math>X_{12}=10\Omega</math>, <math>X_{23}=20\Omega</math>, <math>X_{31}=20\Omega</math>. | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:PEE_M6_Slajd18.png|500px]] | |||
|valign="top"|''Rozwiązanie'' | |||
Ze względu na występowanie sprzężenia magnetycznego pierwszym etapem rozwiązania jest eliminacja tych sprzężeń. Układ odbiornika po likwidacji sprzężeń magnetycznych jest przedstawiony na rysunku obok. | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:PEE_M6_Slajd19.png|500px]] | |||
|valign="top"|Przyjmijmy układ napięć fazowych generatora w następującej postaci | |||
: <math>E_A=400e^{j0}</math> | |||
: <math>E_B=400e^{-j120}</math> | |||
: <math>E_C=400e^{j120}</math> | |||
Impedancje poszczególnych faz odbiornika z rysunku na slajdzie 18 są równe | |||
: <math>Z_A=40+j40=40\sqrt{2}e^{j45^\circ}</math> | |||
: <math>Z_B=j60=60e^{j90^\circ}</math> | |||
: <math>Z_C=0</math> | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:PEE_M6_Slajd20.png|500px]] | |||
|valign="top"|Wobec zwarcia w fazie C odbiornika (<math>Z_C = 0</math>) nie zachodzi potrzeba stosowania wzoru | |||
: <math>U_N={E_AY_A+E_BY_B+E_CY_C \over (Y_A+Y_B+Y_C+Y_N)}</math> | |||
do wyznaczenia napięcia niezrównoważenia, gdyż <math>U_N = E_C</math>. W tej sytuacji poszczególne prądy fazowe są równe | |||
: <math>I_A={E_A-U_N \over Z_A}={400-400e^{j120^\circ} \over 40\sqrt{2}e^{j45^\circ}}=5\sqrt{2}e^{-j75^\circ}=1,8-j6,8</math> | |||
: <math>I_B={E_B-U_N \over Z_B}={400e^{-j120^\circ}-400e^{j120^\circ} \over 60e^{j90^\circ}}=-11,6</math> | |||
: <math>I_C=-I_A-I_B=9,8+j6,8</math> | |||
Po obliczeniu prądów na podstawie schematu zastępczego bez sprzężeń magnetycznych dla wyznaczenia napięć w układzie należy powrócić do obwodu ze sprzężeniami. Rzeczywiste napięcia na fazach odbiornika wynoszą | |||
: <math>U_A=RI_A+jX_LI_A+jX_{12}I_B+jX_{31}I_C=322+j263</math> | |||
: <math>U_B=jX_LI_B+jX_{12}I_A+jX_{23}I_C=-18-j335</math> | |||
: <math>U_C=jX_LI_C+jX_{31}I_A+jX_{23}I_B-jX_CI_C=-18</math> | |||
Zauważmy, że istnieje ogromna różnica między rzeczywistym napięciem <math>U_C</math> w fazie C, <math>U_C=-18</math>, a napięciem w tej samej fazie w obwodzie po likwidacji sprzężeń, <math>U_C=0</math>. Obwód po likwidacji sprzężeń jest równoważny obwodowi oryginalnemu jedynie pod względem prądowym. Napięcia na gałęziach zawierających cewki sprzężone nie odpowiadają ich odpowiednikom w obwodzie bez sprzężeń. | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:PEE_M6_Slajd21.png|500px]] | |||
|valign="top"|Na rysunku obok i animacji poniżej przedstawiono wykres wektorowy prądów i napięć w obwodzie po likwidacji sprzężeń. | |||
[[Grafika:PEE_M6_rys6_15_animacja.gif]] | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:PEE_M6_Slajd22.png|500px]] | |||
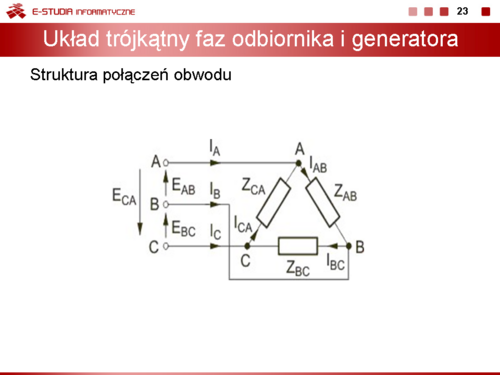
|valign="top"|'''Układ trójkątny faz odbiornika i generatora''' | |||
Schemat elektryczny połączeń elementów obwodu trójfazowego o odbiorniku i generatorze połączonych w trójkąt (układ trójkąt-trójkąt) przedstawia rysunku obok. | |||
|} | |} | ||
| Linia 228: | Linia 356: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika: | |valign="top" width="500px"|[[Grafika:PEE_M6_Slajd23.png|500px]] | ||
|valign="top"| | |valign="top"|Przyjmijmy dla uproszczenia, że impedancje przewodów zasilających poszczególne fazy są zerowe. Oznacza to, że napięcia na fazach odbiornika (włączonych międzyfazowo) są napięciami międzyfazowymi generatora, to jest | ||
: <math>U_{AB}=E_{AB}</math> | |||
: <math>U_{BC}=E_{BC}</math> | |||
: <math>U_{CA}=E_{CA}</math> | |||
Stąd przy zadanych wartościach impedancji odbiornika prądy fazowe tego odbiornika są określone wzorami | |||
: <math>I_{AB}=Y_{AB}E_{AB}</math> | |||
: <math>I_{BC}=Y_{BC}E_{BC}</math> | |||
: <math>I_{CA}=Y_{CA}E_{CA}</math> | |||
Prądy przewodowe zasilające obwód trójkątny odbiornika mogą być wyznaczone z zależności | |||
: <math>I_A=I_{AB}-I_{CA}</math> | |||
: <math>I_B=I_{BC}-I_{AB}</math> | |||
: <math>I_C=I_{CA}-I_{BC}</math> | |||
Zauważmy, że wobec powyższych wzorów suma prądów przewodowych w układzie, niezależnie od wartości impedancji odbiornika jest równa zeru | |||
: <math>I_A+I_B+I_C=0</math> | |||
|} | |} | ||
| Linia 235: | Linia 389: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika: | |valign="top" width="500px"|[[Grafika:PEE_M6_Slajd24.png|500px]] | ||
|valign="top"| | |valign="top"|Animacja poniżej oraz slajd obok przedstawiają wykres wektorowy prądów i napięć w układzie trójfazowym o połączeniu trójkątnym. | ||
[[Grafika:PEE_M6_anim_8.gif]] | |||
|} | |} | ||
| Linia 242: | Linia 398: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika: | |valign="top" width="500px"|[[Grafika:PEE_M6_Slajd24a.png|500px]] | ||
|valign="top"| | |valign="top"| | ||
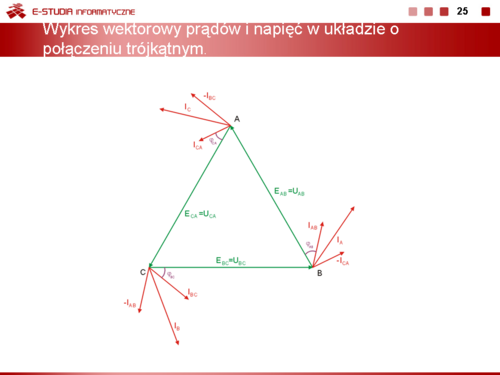
W przypadku pełnej symetrii generatora i odbiornika wszystkie układy napięć i prądów w układzie będą również symetryczne a przesunięcia między prądami oraz napięciami poszczególnych faz w odpowiednich układach będą równe <math>120^\circ</math>. Interesująca jest wówczas relacja między prądami fazowymi oraz liniowymi układu. Z wykresu wektorowego przedstawionego na wcześniejszym rysunku widać, że w przypadku symetrycznym moduły wszystkich prądów liniowych są sobie równe, podobnie jak moduły wszystkich prądów fazowych przy równych przesunięciach fazowych między wektorami o kąt <math>120^\circ</math>. Z analizy przesunięć kątowych wynika, że kąt między wektorem prądu fazowego <math>I_f</math> oraz liniowego <math>I_l</math> jest równy <math>30^\circ</math>. Z zależności trygonometrycznych wynika, że | |||
: <math>{0,5|I_l| \over |I_f|}=cos30^\circ</math> | |||
skąd po prostych przekształceniach matematycznych otrzymuje się | |||
: <math>|I_l|=2|I_f|cos30^\circ=\sqrt{3}|I_f|</math> | |||
W układzie symetrycznym prąd liniowy jest <math>\sqrt{3}</math> razy większy niż prąd fazowy. Jest to identyczna relacja jaka istnieje między napięciami fazowymi i międzyfazowymi (liniowymi). | |||
|} | |} | ||
| Linia 249: | Linia 414: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika: | |valign="top" width="500px"|[[Grafika:PEE_M6_Slajd25.png|500px]] | ||
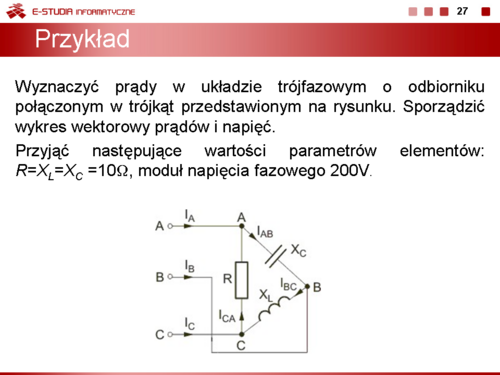
|valign="top"| | |valign="top"|Jako przykład wyznaczymy prądy w układzie trójfazowym o odbiorniku połączonym w trójkąt przedstawionym na rysunku obok (slajd 25). Należy również sporządzić wykres wektorowy prądów i napięć. Przyjąć następujące wartości parametrów elementów: <math>|E_f|=200V</math>, <math>R=X_L=X_C =10\Omega</math>. | ||
|} | |} | ||
| Linia 256: | Linia 422: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika: | |valign="top" width="500px"|[[Grafika:PEE_M6_Slajd26.png|500px]] | ||
|valign="top"| | |valign="top"|Napięcia międzyfazowe: | ||
: <math>|E_{mf}|=\sqrt{3}|E_f|</math> | |||
: <math>E_{AB}=200\sqrt{3}</math> | |||
: <math>E_{BC}=200\sqrt{3}e^{-j120^\circ}</math> | |||
: <math>E_{CA}=200\sqrt{3}e^{j120^\circ}</math> | |||
Prądy fazowe odbiornika: | |||
: <math>I_{AB}={E_{AB} \over -jX_C}=20\sqrt{3}e^{j90^\circ}</math> | |||
: <math>I_{BC}={E_{BC} \over jX_L}=20\sqrt{3}e^{-j210^\circ}</math> | |||
: <math>I_{CA}={E_{CA} \over R}=20\sqrt{3}e^{j120^\circ}</math> | |||
Prądy liniowe układu: | |||
: <math>I_A=I_{AB}-I_{CA}=17,32+j4,64</math> | |||
: <math>I_B=I_{BC}-I_{AB}=-30-j17,32</math> | |||
: <math>I_C=I_{CA}-I_{BC}=12,68+j12,68</math> | |||
|} | |} | ||
| Linia 263: | Linia 455: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika: | |valign="top" width="500px"|[[Grafika:PEE_M6_Slajd27.png|500px]] | ||
|valign="top"| | |valign="top"|Wykres wektorowy prądów i napięć przedstawiony jest na rysunku poniżej oraz na slajdzie obok. | ||
[[Grafika:PEE_M6_anim_9.gif ]] | |||
|} | |} | ||
| Linia 270: | Linia 465: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika: | |valign="top" width="500px"|[[Grafika:PEE_M6_Slajd28.png|500px]] | ||
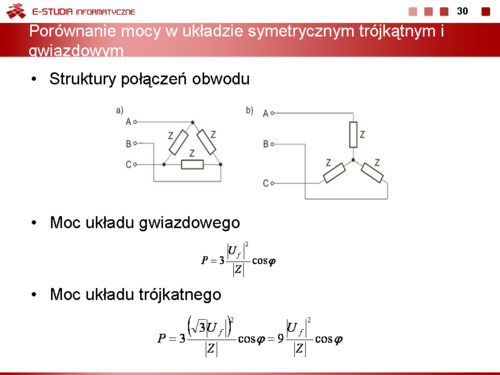
|valign="top"| | |valign="top"|Przełączenie impedancji odbiornika z połączenia trójkątnego w gwiazdowe powoduje zmianę mocy wydzielonej w odbiorniku. Załóżmy dla uproszczenia, że obwód trójfazowy jest symetryczny o impedancji fazy równej <math>Z\ </math>,. Schemat połączenia trójkątny i gwiazdowy impedancji przedstawiony jest na rysunku obok. | ||
Jak łatwo pokazać dla układu trójkątnego moc czynna <math>P\ </math>, układu jest równa | |||
: <math>P=3{(\sqrt{3}|U_f|)^2 \over |Z|}\cos \varphi = 9{|U_f|^2 \over |Z|}\cos \varphi</math> | |||
natomiast w układzie gwiazdowym wobec <math>U_N = 0</math> mamy | |||
: <math>P=3{|U_f|^2 \over |Z|}\cos \varphi</math> | |||
Jak wynika z powyższych wzorów przy przełączeniu odbiornika symetrycznego z gwiazdy na trójkąt pobór mocy czynnej wzrasta 3-krotnie. Przy tej samej wartości impedancji w obu połączeniach oznacza to <math>\sqrt{3}</math>-krotny wzrost prądu płynącego przez impedancję. | |||
|} | |} | ||
| Linia 277: | Linia 483: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"| | |valign="top" width="500px"|<applet code="dyplom.Applet1.class" archive="images/6/64/Dyplom.jar" width="640" height="480"> | ||
|valign="top"| | </applet> | ||
|valign="top"|Do obliczeń prądów, napięć i mocy w obwodach trójfazowych został opracowany program „Obwody trójfazowe” umieszczony obok. Pozwala on na symulację pracy układu trójfazowego o dowolnej strukturze połączeń. | |||
Centralne pole programu zajmuje schemat badanego obwodu (dostępne konfiguracje: gwiazda-gwiazda <math>Y-Y\ </math>,, gwiazda-trójkąt <math>Y-\Delta</math>, trójkąt-trójkąt <math>\;\Delta-\Delta\;</math> i trójkąt-gwiazda <math>\Delta-Y</math>), z symbolicznie zaznaczonym odbiornikiem i zasilaniem trójfazowym. | |||
Działanie programu rozpoczyna się po wybraniu odpowiedniej opcji obliczeń. Użytkownik może definiować własną strukturę obwodu (<math>\Delta\ </math>,,<math>Y\ </math>,, przewód zerowy), rodzaj i wartości parametrów odbiornika (R, L, C), wartości źródeł wymuszających, impedancję przewodu zerowego, format liczb zespolonych. | |||
W wyniku obliczeń otrzymuje się wartości prądów, napięć i mocy w obwodzie, jak również wykres wektorowy prądów i napięć oraz ich przebiegi czasowe. Program stanowi efektywne wirtualne laboratorium obwodów trójfazowych, umożliwiające studentowi samodzielne badanie zjawisk zachodzących w obwodach trójfazowych. | |||
|} | |} | ||
<hr width="100%"> | |||
'''Zadania sprawdzające''' | |||
''Zadanie 6.1'' | |||
Wyznaczyć prądy w obwodzie trójfazowym podanym na rysunku poniżej. Przyjąć następujące wartości parametrów elementów: <math>|E_f|=200V</math>, <math>Z_A=10\Omega</math>, <math>Z_B=(10-j10)\Omega</math>, <math>Z_C=(10+j10)\Omega</math>, <math>Z_N=50\Omega</math>. | |||
[[Grafika:PEE_M4_zadanie_6_1.png]] | |||
''Rozwiązanie'' | |||
Przyjmujemy następujące wartości symboliczne elementów: | |||
: <math>E_A=200</math> | |||
: <math>E_B=200e^{-j120^\circ}</math> | |||
: <math>E_C=200e^{j120^\circ}</math> | |||
: <math>Y_A={1 \over Z_A}=0,1</math> | |||
: <math>Y_B={1 \over Z_B}=0,05+j0,05</math> | |||
: <math>Y_C={1 \over Z_C}=0,05-j0,05</math> | |||
: <math>Y_N={1 \over Z_N}=0,02</math> | |||
Napięcie niezrównoważenia <math>U_N</math> | |||
: <math>U_N={E_AY_A+E_BY_B+E_CY_C \over Y_A+Y_B+Y_C+Y_N}=124,18</math> | |||
Prądy fazowe: | |||
: <math>I_A=(E_A-U_N)Y_A=7,58</math> | |||
: <math>I_B=(E_B-U_N)Y_B=-2,55-j19,87</math> | |||
: <math>I_C=(E_C-U_N)Y_C=2,55+j19,87</math> | |||
: <math>I_N=U_NY_N=2,48</math> | |||
Aktualna wersja na dzień 12:04, 5 wrz 2023

|

|
Przyjmijmy układ napięć fazowych generatora w następującej postaci
|
|
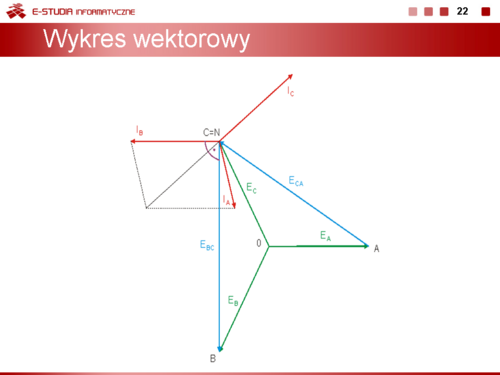
Na rysunku obok i animacji poniżej przedstawiono wykres wektorowy prądów i napięć w obwodzie po likwidacji sprzężeń. |
|
Animacja poniżej oraz slajd obok przedstawiają wykres wektorowy prądów i napięć w układzie trójfazowym o połączeniu trójkątnym. |

|
Napięcia międzyfazowe:
|
|
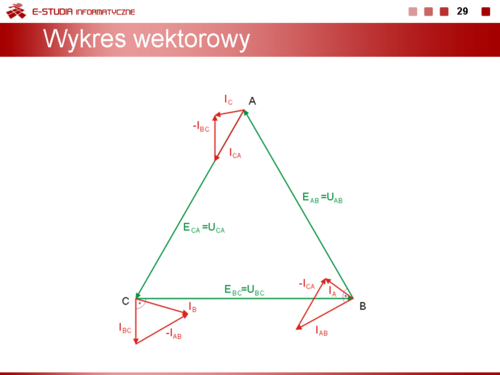
Wykres wektorowy prądów i napięć przedstawiony jest na rysunku poniżej oraz na slajdzie obok. |
| <applet code="dyplom.Applet1.class" archive="images/6/64/Dyplom.jar" width="640" height="480">
</applet> |
Do obliczeń prądów, napięć i mocy w obwodach trójfazowych został opracowany program „Obwody trójfazowe” umieszczony obok. Pozwala on na symulację pracy układu trójfazowego o dowolnej strukturze połączeń.
Centralne pole programu zajmuje schemat badanego obwodu (dostępne konfiguracje: gwiazda-gwiazda ,, gwiazda-trójkąt , trójkąt-trójkąt i trójkąt-gwiazda ), z symbolicznie zaznaczonym odbiornikiem i zasilaniem trójfazowym. Działanie programu rozpoczyna się po wybraniu odpowiedniej opcji obliczeń. Użytkownik może definiować własną strukturę obwodu (,,,, przewód zerowy), rodzaj i wartości parametrów odbiornika (R, L, C), wartości źródeł wymuszających, impedancję przewodu zerowego, format liczb zespolonych. W wyniku obliczeń otrzymuje się wartości prądów, napięć i mocy w obwodzie, jak również wykres wektorowy prądów i napięć oraz ich przebiegi czasowe. Program stanowi efektywne wirtualne laboratorium obwodów trójfazowych, umożliwiające studentowi samodzielne badanie zjawisk zachodzących w obwodach trójfazowych. |
Zadania sprawdzające
Zadanie 6.1
Wyznaczyć prądy w obwodzie trójfazowym podanym na rysunku poniżej. Przyjąć następujące wartości parametrów elementów: , , , , .
Rozwiązanie
Przyjmujemy następujące wartości symboliczne elementów:
Napięcie niezrównoważenia
Prądy fazowe: