PEE Moduł 6: Różnice pomiędzy wersjami
Nie podano opisu zmian |
m Zastępowanie tekstu – „\</math>” na „\ </math>” |
||
| (Nie pokazano 23 wersji utworzonych przez 3 użytkowników) | |||
| Linia 1: | Linia 1: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika: | |valign="top" width="500px"|[[Grafika:PEE_M6_Slajd1.png|500px]] | ||
|valign="top"| | |valign="top"| | ||
|} | |} | ||
| Linia 7: | Linia 7: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika: | |valign="top" width="500px"|[[Grafika:PEE_M6_Slajd2.png|500px]] | ||
|valign="top"| | |valign="top"|'''Definicja układu trójfazowego''' | ||
'''Definicja układu trójfazowego''' | |||
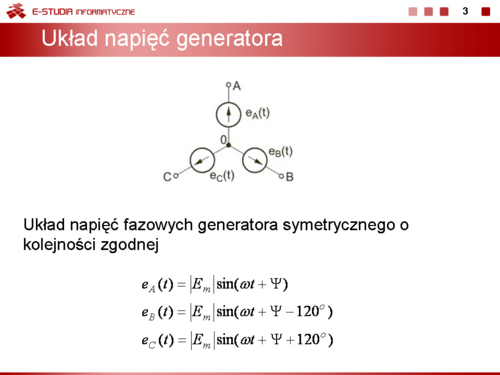
Układem trójfazowym nazywamy układ trzech obwodów elektrycznych, w których istnieją trzy źródła napięć sinusoidalnych o jednakowej częstotliwości, przesunięte względem siebie o określony kąt fazowy i wytworzone w jednym generatorze zwanym generatorem trójfazowym. Poszczególne obwody generatora trójfazowego nazywać będziemy '''fazami''' i oznaczać literami A, B, C lub kolejnymi cyframi 1, 2, 3. | Układem trójfazowym nazywamy układ trzech obwodów elektrycznych, w których istnieją trzy źródła napięć sinusoidalnych o jednakowej częstotliwości, przesunięte względem siebie o określony kąt fazowy i wytworzone w jednym generatorze zwanym generatorem trójfazowym. Poszczególne obwody generatora trójfazowego nazywać będziemy '''fazami''' i oznaczać literami A, B, C lub kolejnymi cyframi 1, 2, 3. | ||
| Linia 18: | Linia 16: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika: | |valign="top" width="500px"|[[Grafika:PEE_M6_Slajd3.png|500px]] | ||
|valign="top"|Przykład połączenia 3 faz generatora w jeden układ gwiazdowy przedstawiony jest na rysunku obok (slajd 3). | |valign="top"|Przykład połączenia 3 faz generatora w jeden układ gwiazdowy przedstawiony jest na rysunku obok (slajd 3). | ||
| Linia 24: | Linia 22: | ||
: <math>e_A(t)=|E_m|sin(\omega t+\Psi)</math> | : <math>e_A(t)=|E_m|sin(\omega t+\Psi)</math> | ||
: <math>e_B(t)=|E_m|sin(\omega t+\Psi-120^\circ)</math> | : <math>e_B(t)=|E_m|sin(\omega t+\Psi-120^\circ)</math> | ||
: <math>e_C(t)=|E_m|sin(\omega t+\Psi+120^\circ)</math> | : <math>e_C(t)=|E_m|sin(\omega t+\Psi+120^\circ)</math> | ||
| Linia 33: | Linia 33: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika: | |valign="top" width="500px"|[[Grafika:PEE_M6_Slajd4.png|500px]] | ||
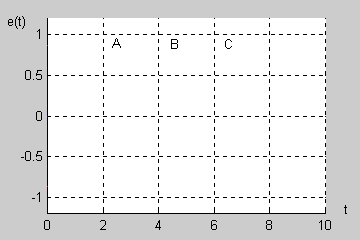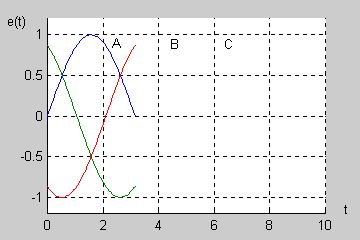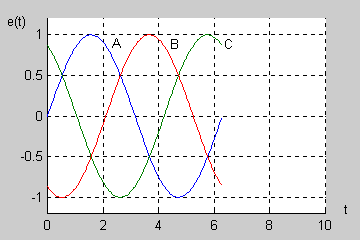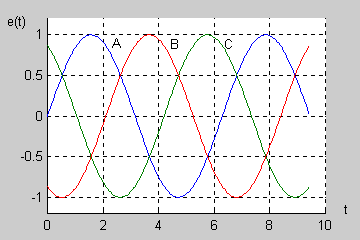
|valign="top"|W normalnym systemie trójfazowym przyjmuje się tzw. '''kolejność wirowania zgodną''', w której faza B opóźnia się względem fazy A o kąt <math>120^\circ</math> a faza C (opóźniona względem fazy B o kolejny kąt <math>120^\circ</math> ) wyprzedza fazę A o kąt równy <math>120^\circ</math>. | |||
Na rysunku obok (slajd 4) i na aminacji poniżej przedstawiono przebiegi czasowe napięć trójfazowych przy kącie początkowym <math>\Psi\ </math>, równym zeru. Napięcia są zmienne sinusoidalnie przy czym występują regularne przesunięcia o kąt <math>120^\circ</math> między poszczególnymi sinusoidami. | |||
[[Grafika:PEE_M6_anim_1.gif]] | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:PEE_M6_Slajd5.png|500px]] | |||
|valign="top"|'''Układ napięć fazowych''' | |||
Wobec sinusoidalnej postaci wymuszeń w analizie układów trójfazowych zastosujemy metodę symboliczną. Zgodnie z tą metodą napięcia sinusoidalne zastępuje się ich postacią zespoloną, która dla przyjętych funkcji sinusoidalnych może być zapisana następująco | |||
: <math>E_A={|E_m| \over \sqrt{2}}e^{j\Psi}</math> | |||
: <math>E_B={|E_m| \over \sqrt{2}}e^{j(\Psi-120^\circ)}=E_Ae^{-j120^\circ}</math> | |||
: <math>E_A={|E_m| \over \sqrt{2}}e^{j(\Psi+120^\circ)}=E_Ae^{j120^\circ}</math> | |||
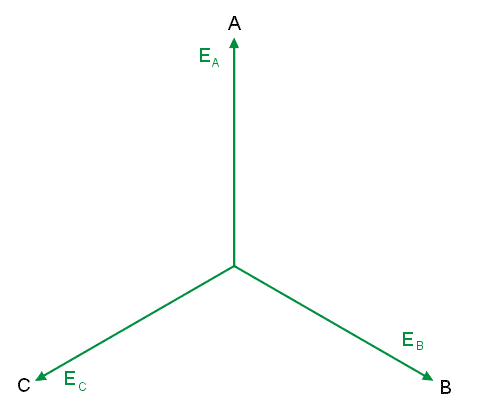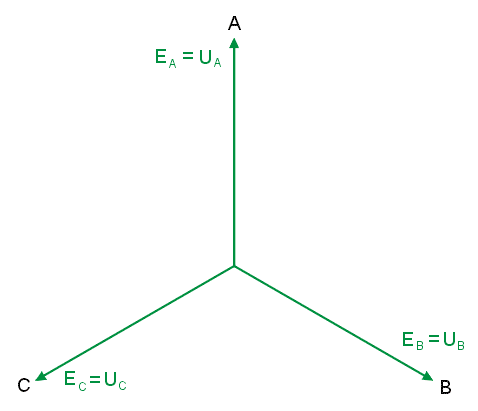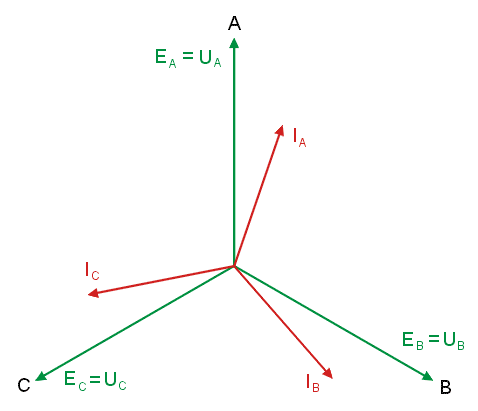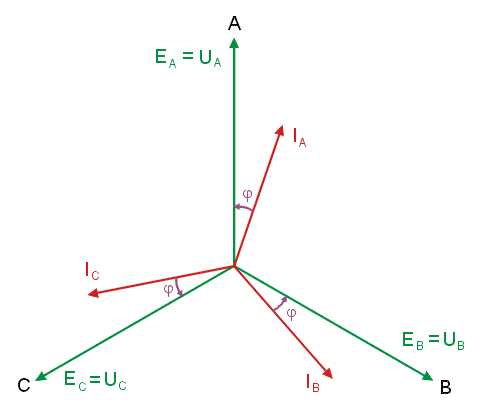
W praktyce wobec nieustannej zmiany wartości napięć w czasie faza początkowa <math>\Psi</math> może być przyjęta dowolnie. Najczęściej dla wygody zakładać będziemy, że jest równa zeru. Wykres wektorowy napięć trójfazowych opisanych powyższymi zależnościami dla kąta fazowego <math>\Psi \neq 0</math> przedstawiony jest na rysunku obok (slajd 5). | |||
Punkt wspólny napięć, odpowiadający wspólnemu punktowi połączenia faz generatora oznaczony jest cyfrą 0. Na końcach napięć fazowych zaznaczone są oznaczenia faz (A, B, C). Napięcie fazowe generatora to napięcie między punktem końcowym wektora a punktem zerowym. | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:PEE_M6_Slajd6.png|500px]] | |||
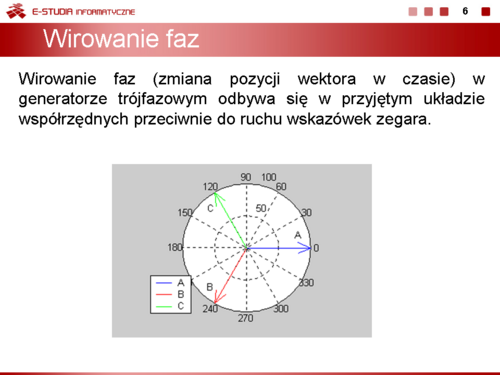
|valign="top"|Wirowanie faz (zmiana pozycji wektora w czasie) w generatorze trójfazowym odbywa się w przyjętym układzie współrzędnych przeciwnie do ruchu wskazówek zegara. | |||
[[Grafika:PEE_M6_anim_2.gif]] | |||
Rysunek powyżej pokazuje wektory napięć generatora trójfazowego wirujące w czasie. Wektory fazy B i C nadążają za wektorem A, przy czym przesunięcia fazowe między nimi są stałe i równe dokładnie <math>120^\circ</math>. Ważną cechą trójfazowego generatora symetrycznego jest zerowanie się sumy napięć fazowych | |||
: <math>E_A+E_B+E_C=0</math> | |||
Wartość zerowa sumy wynika bezpośrednio z symetrii poszczególnych napięć. Mianowicie | |||
: <math>E_A+E_B+E_C=E_A+E_Ae^{-j120^\circ}+E_Ae^{j120^\circ}=</math> | |||
: <math>E_A \left ( 1-0,5-j{\sqrt{3} \over 2}-0,5+j{\sqrt{3} \over 2} \right )=0</math> | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:PEE_M6_Slajd7.png|500px]] | |||
|valign="top"|'''Układ napięć międzyfazowych''' | |||
Oprócz napięć fazowych wyróżnia się układ '''napięć międzyfazowych''', zwanych również liniowymi, czyli napięć panujących między punktami zewnętrznymi poszczególnych faz. Przy trzech napięciach fazowych można wyróżnić trzy napięcia międzyfazowe: <math>E_{AB}</math>, <math>E_{BC}</math> oraz <math>E_{CA}</math>, przy czym | |||
: <math>E_{AB}=E_A-E_B</math> | |||
: <math>E_{BC}=E_B-E_C</math> | |||
: <math>E_{CA}=E_C-E_A</math> | |||
Z definicji napięć międzyfazowych wynika, że niezależnie od symetrii ich suma jest zawsze równa zeru gdyż wszystkie napięcia tworzą trójkąt zamknięty. Rysunek na sladzie nr 7 pokazuje układ napięć międzyfazowych generatora trójfazowego z przyjętymi oznaczeniami. Symbol <math>E_{AB}\ </math>, oznacza, że strzałka wektora napięcia na wykresie jest skierowana w stronę pierwszego wskaźnika w oznaczeniu (u nas litera A). Z symetrii napięć fazowych wynika bezpośrednio symetria napięć międzyfazowych. Napięcia te są równe i przesunięte względem siebie o kąt <math>120^\circ</math>, czyli | |||
: <math>E_{AB}=E_A-E_B</math> | |||
: <math>E_{BC}=E_{AB}e^{-j120^\circ}</math> | |||
: <math>E_{CA}=E_{AB}e^{j120^\circ}</math> | |||
Układ napięć międzyfazowych symetrycznych tworzy więc trójkąt równoboczny. Wykorzystując relacje obowiązujące dla tego trójkąta łatwo jest udowodnić, że napięcie międzyfazowe jest <math>\sqrt{3}\ </math>, razy większe niż napięcie fazowe, co zapiszemy w ogólności jako | |||
: <math>|E_{mf}|=\sqrt{3}|E_f|</math> | |||
gdzie <math>|E_f|</math> oznacza moduł napięcia fazowego a <math>|E_{mf}|</math> moduł napięcia międzyfazowego. | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:PEE_M6_Slajd8.png|500px]] | |||
|valign="top"|'''Połączenia trójfazowe generatora i odbiornika''' | |||
Układ napięć fazowych generatora może być połączony bądź w gwiazdę bądź w trójkąt. Schemat obu połączeń przedstawiony jest na rysunku obok (slajd nr 8). | |||
Przy połączeniu trójkątnym generatora odbiornik jest zasilany napięciem międzyfazowym trójprzewodowym. Przy połączeniu generatora w gwiazdę napięcie zasilające jest napięciem fazowym a liczba przewodów może być równa trzy bądź cztery (przy czterech przewodach zasilających jednym z nich jest przewód zerowy, zwany również przewodem neutralnym). | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:PEE_M6_Slajd9.png|500px]] | |||
|valign="top"|W układzie trójfazowym odbiornik zawiera również trzy fazy, przy czym może być on połączony w gwiazdę lub w trójkąt. Oba sposoby połączenia odbiornika przedstawione są na dolnym rysunku na slajdzie nr 8. | |||
W zależności od sposobu połączenia generatora i odbiornika można w układach trójfazowych wyróżnić cztery rodzaje połączeń. Są to: | |||
*generator i odbiornik połączone w gwiazdę (układ gwiazdowy) | |||
*generator i odbiornik połączone w trójkąt (układ trójkątny) | |||
*generator połączony w gwiazdę a odbiornik w trójkąt | |||
*generator połączony w trójkąt a odbiornik w gwiazdę. | |||
Z punktu widzenia metodyki analizy obwodów istotne są tylko dwa pierwsze rodzaje połączeń. Dwa pozostałe są wtórne względem pierwszych i nie wnoszą nowych elementów do metody analizy. | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:PEE_M6_Slajd10.png|500px]] | |||
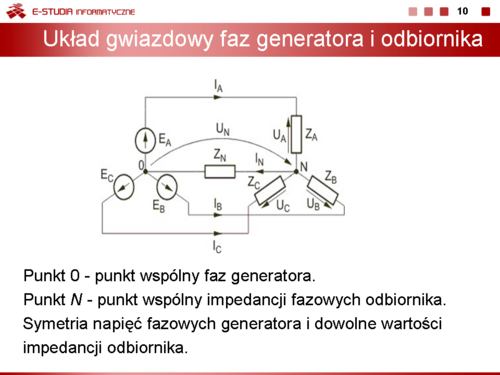
|valign="top"|'''Układ gwiazdowy faz generatora i odbiornika''' | |||
Rozpatrzmy układ połączeń gwiazdowych odbiornika i generatora (gwiazda-gwiazda) z oznaczeniami prądów i napięć przedstawionymi na rysunku obok (slajd nr 10). | |||
Punkt 0 oznacza punkt wspólny faz generatora. Punkt <math>N\ </math>, jest punktem wspólnym impedancji fazowych odbiornika. Zakładamy symetrię napięć fazowych generatora i dowolne wartości impedancji odbiornika. Przyjmijmy do analizy układ czteroprzewodowy z impedancją przewodu zerowego równa <math>Z_N</math>. Wartość impedancji <math>Z_N</math> może być dowolna, w szczególności zerowa (bezpośrednie zwarcie punktów wspólnych generatora i odbiornika) lub nieskończona (układ trójprzewodowy bez przewodu zerowego). Napięcie między punktem zerowym odbiornika i generatora oznaczymy przez <math>U_N</math> i nazywać będziemy '''napięciem niezrównoważenia'''. | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:PEE_M6_Slajd11.png|500px]] | |||
|valign="top"|Układ napięć trójfazowych odbiornika tworzą napięcia na poszczególnych jego fazach, czyli <math>U_A</math>, <math>U_B</math>, <math>U_C</math>. W efekcie w obwodzie trójfazowym o połączeniu gwiazda-gwiazda wyróżnia się dwa układy napięć trójfazowych gwiazdowych: generatora <math>E_A</math>, <math>E_B</math>, <math>E_C</math> i odbiornika <math>U_A</math>, <math>U_B</math>, <math>U_C</math>. | |||
Dla obliczenia prądów w obwodzie należy wyznaczyć układ napięć odbiornikowych. Najlepiej dokonać tego wyznaczając napięcie <math>U_N</math>. Zastosujemy metodę potencjałów węzłowych przy założeniu, że punkt 0 jest węzłem odniesienia a poszukiwany potencjał węzłowy jest równy <math>U_N</math>. Zgodnie z metodą potencjałów węzłowych otrzymuje się | |||
: <math>E_AY_A+E_BY_B+E_CY_C=U_N(Y_A+Y_B+Y_C+Y_N)</math> | |||
Stąd | |||
: <math>U_N={E_AY_A+E_BY_B+E_CY_C \over (Y_A+Y_B+Y_C+Y_N)}</math> | |||
gdzie wielkości oznaczone symbolem <math>Y\ </math>, są admitancjami: <math>Y_A={1 \over Z_A}</math>, <math>Y_B={1 \over Z_B}</math>, <math>Y_C={1 \over Z_C}</math> oraz <math>Y_N={1 \over Z_N}</math>. Wyznaczenie wartości napięcia <math>U_N</math> pozwala obliczyć wartości napięć odbiornikowych. Z prawa napięciowego Kirchhoffa napisanego dla trzech oczek w obwodzie wynika | |||
: <math>U_A=E_A-U_N</math> | |||
: <math>U_B=E_B-U_N</math> | |||
: <math>U_C=E_C-U_N</math> | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:PEE_M6_Slajd11a.png|500px]] | |||
|valign="top"|Przy znanych wartościach admitancji odbiornika obliczenie prądu polega na zastosowaniu prawa Ohma. Mianowicie | |||
: <math>I_A=Y_AU_A</math> | |||
: <math>I_B=Y_BU_B</math> | |||
: <math>I_C=Y_CU_C</math> | |||
: <math>I_N=Y_NU_N</math> | |||
Suma prądów w węźle <math>N\ </math>, jest równa zeru, zatem <math>I_A+I_B+I_C=I_N</math>. Moce wydzielone w odbiorniku trójfazowym oblicza się jako sumę mocy wydzielonych w poszczególnych fazach odbiornika, czyli | |||
: <math>S_A=P_A+jQ_A=U_AI_A^*</math> | |||
: <math>S_B=P_B+jQ_B=U_BI_B^*</math> | |||
: <math>S_C=P_C+jQ_C=U_CI_C^*</math> | |||
Moc wydzielona na impedancji przewodu zerowego oznacza moc strat. Jest ona równa | |||
: <math>S_N=P_N+jQ_N=U_NI_N^*</math> | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:PEE_M6_Slajd12.png|500px]] | |||
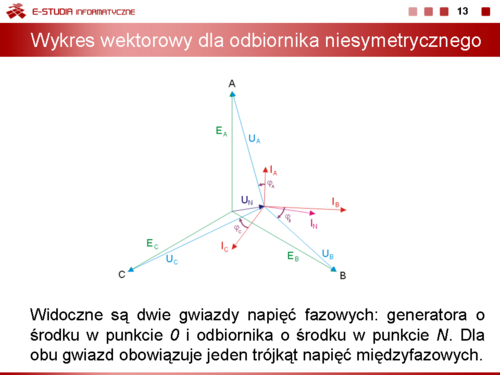
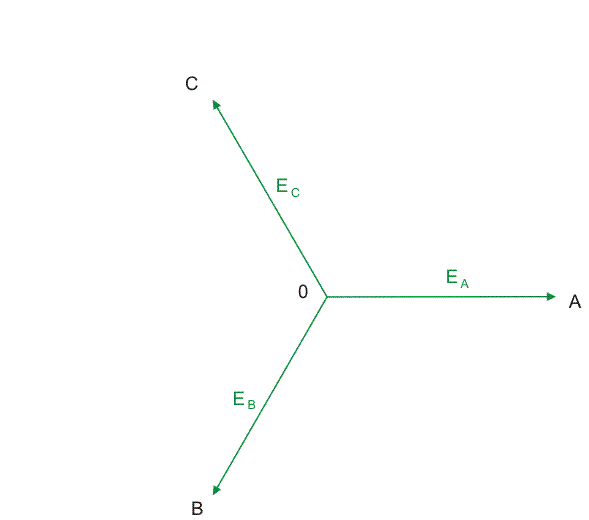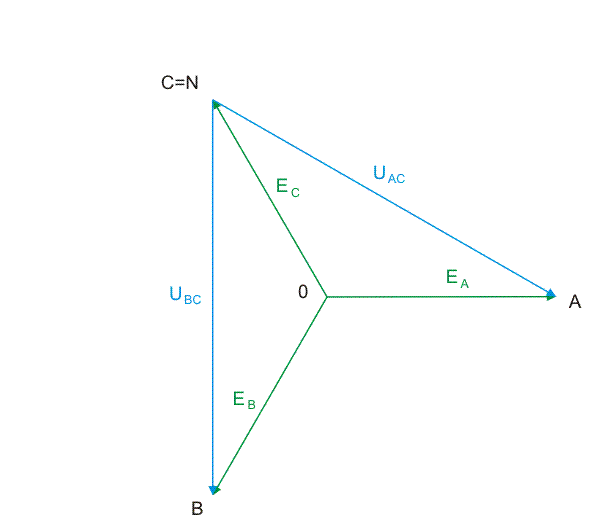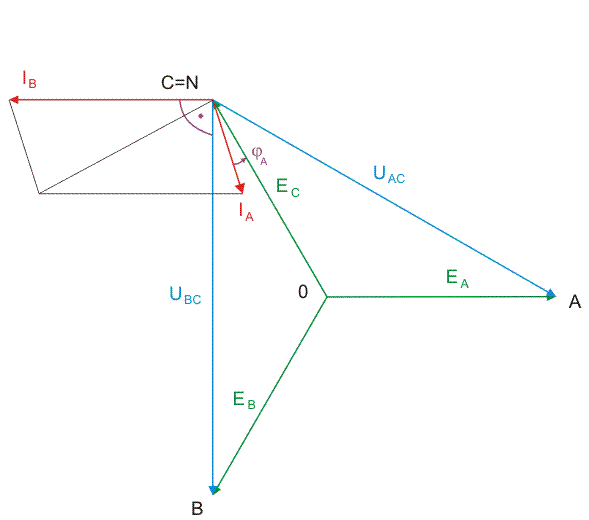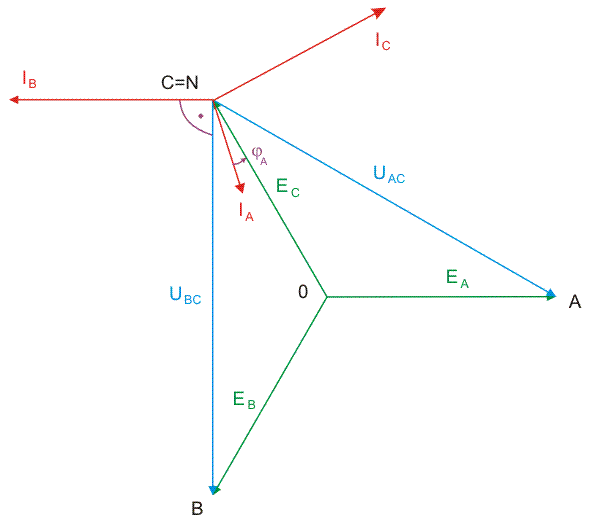
|valign="top"|Otrzymane wyniki można zinterpretować na wykresie wektorowym prądów i napięć w obwodzie. | |||
Rysunek na slajdzie obok przedstawia wykres wektorowy prądów i napięć dla przypadku obciążenia niesymetrycznego. Animacja poniżej przedstawia sposób konstrukcji wykresu wektorowego. | |||
[[Grafika:PEE_M6_anim_3.gif]] | |||
Widoczne są dwie gwiazdy napięć fazowych: generatora o środku w punkcie <math>0\ </math>, i odbiornika o środku w punkcie <math>N\ </math>,. Dla obu gwiazd obowiązuje jeden trójkąt napięć międzyfazowych. Przesunięcie potencjału punktu <math>N\ </math>, względem <math>0\ </math>, (napięcie <math>U_N</math> różne od zera) jest spowodowane niesymetrią odbiornika. | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:PEE_M6_Slajd13.png|500px]] | |||
|valign="top"|W pracy układu trójfazowego gwiazdowego można wyróżnić kilka szczególnych przypadków. | |||
* '''Odbiornik symetryczny''' (<math>Z_A=Z_B=Z_C=Z</math>) z dowolną wartością impedancji przewodu zerowego | |||
W tym przypadku napięcie niezrównoważenia jest równe zeru a anpięcia fazowe odbiornika są równe napięciom fazowym generatora. Prądy w takim przypadku oblicza się ze wzorów podanych na slajdzie obok. Prąd przewodu zerowego <math>I_N=0</math>. Wszystkie prądy fazowe są równe co do amplitydy i przesunięte w fazie o <math>120^\circ</math>. | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:PEE_M6_Slajd14.png|500px]] | |||
|valign="top"|Rysunek na slajdzie obok przedstawia wykres wektorowy prądów i napięć dla tego przypadku. Animacja poniżej przedstawia sposób konstrukcji wykresu wektorowego. | |||
[[Grafika:PEE_M6_anim_4.gif]] | |||
Odbiornik symetryczny jest jednym z częściej występujących przypadków w praktyce. Przykładami takich odbiorników są: silniki elektryczne trójfazowe czy piece grzejne trójfazowe (zwykle o dużej mocy). | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:PEE_M6_Slajd15.png|500px]] | |||
|valign="top"| | |valign="top"| | ||
*'''Odbiornik niesymetryczny przy zwartym przewodzie zerowym''' | |||
W tym przypadku napięcie niezrównoważenia <math>U_N=0</math>, a prąd przewodu zerowego w ogólnym przypadku <math>I_N \neq 0</math>. Prądy fazowe są wówczas określane bezpośrednio na podstawie układu napięć generatorowych. Suma tych prądów w ogólnym przypadku odbiornika niesymetrycznego jest różna od zera | |||
: <math>I_N = I_A+I_B+I_C</math> | |||
Wykres wektorowy prądów i napięć w układzie trójfazowym niesymetrycznym przy zwarciu bezimpedancyjnym punktów wspólnych odbiornika i generatora przedstawiony jest na rysunku poniżej oraz na slajdzie obok. | |||
[[Grafika:PEE_M6_anim_5.gif]] | |||
|} | |} | ||
| Linia 40: | Linia 252: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika: | |valign="top" width="500px"|[[Grafika:PEE_M6_Slajd16.png|500px]] | ||
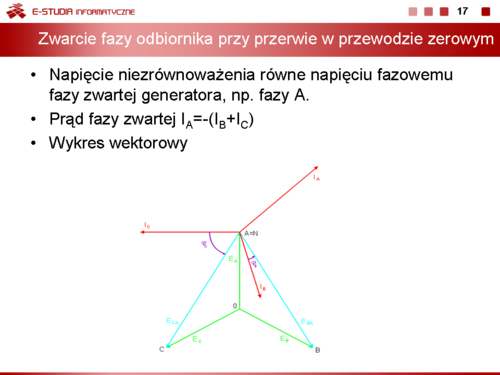
|valign="top"| | |valign="top"|*'''Zwarcie fazy odbiornika przy przerwie w przewodzie zerowym''' | ||
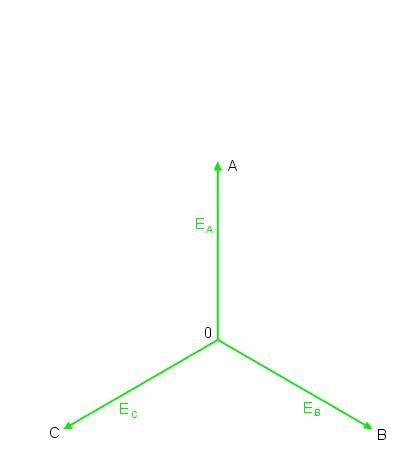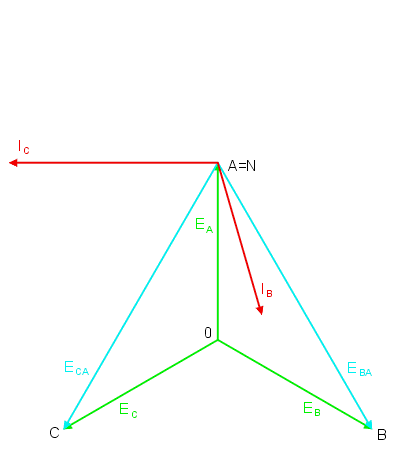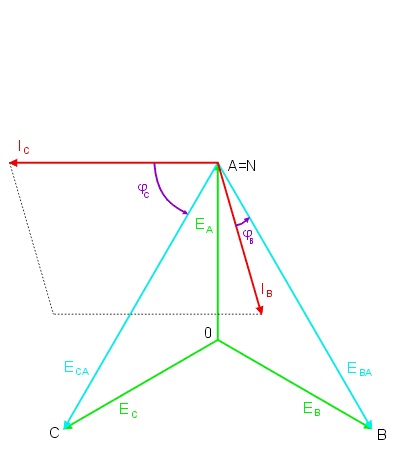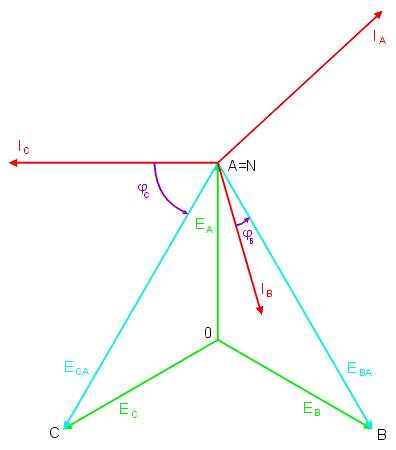
W tym przypadku napięcie niezrównoważenia jest równe napięciu fazowemu fazy zwartej. | |||
Prąd fazy zwartej nie może być określony z prawa Ohma, gdyż zarówno napięcie na fazie odbiornika jak i jego impedancja są równe zeru. Okresla sie go z prawa prądowego Kirchhoffa, zgodnie z którym | |||
: <math>I_A=-I_B-I_C</math> | |||
Wykres wektorowy prądów i napięć w układzie trójfazowym dla przypadku zwarcia fazy A odbiornika przedstawiony jest na rysunku poniżej oraz na slajdzie obok. | |||
[[Grafika:PEE_M6_anim_6.gif]] | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:PEE_M6_Slajd17.png|500px]] | |||
|valign="top"|Jako przykład obliczymy prądy i napięcia poszczególnych faz odbiornika w układzie przedstawionym na rysunku obok. Przyjmiemy zasilanie trójfazowe symetryczne o napięciu fazowym równym <math>400V</math>. Wartości parametrów obwodu są następujące: <math>R=40\Omega</math>, <math>X_C=30\Omega</math>, <math>X_L=60\Omega</math>, <math>X_{12}=10\Omega</math>, <math>X_{23}=20\Omega</math>, <math>X_{31}=20\Omega</math>. | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:PEE_M6_Slajd18.png|500px]] | |||
|valign="top"|''Rozwiązanie'' | |||
Ze względu na występowanie sprzężenia magnetycznego pierwszym etapem rozwiązania jest eliminacja tych sprzężeń. Układ odbiornika po likwidacji sprzężeń magnetycznych jest przedstawiony na rysunku obok. | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:PEE_M6_Slajd19.png|500px]] | |||
|valign="top"|Przyjmijmy układ napięć fazowych generatora w następującej postaci | |||
: <math>E_A=400e^{j0}</math> | |||
: <math>E_B=400e^{-j120}</math> | |||
: <math>E_C=400e^{j120}</math> | |||
Impedancje poszczególnych faz odbiornika z rysunku na slajdzie 18 są równe | |||
: <math>Z_A=40+j40=40\sqrt{2}e^{j45^\circ}</math> | |||
: <math>Z_B=j60=60e^{j90^\circ}</math> | |||
: <math>Z_C=0</math> | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:PEE_M6_Slajd20.png|500px]] | |||
|valign="top"|Wobec zwarcia w fazie C odbiornika (<math>Z_C = 0</math>) nie zachodzi potrzeba stosowania wzoru | |||
: <math>U_N={E_AY_A+E_BY_B+E_CY_C \over (Y_A+Y_B+Y_C+Y_N)}</math> | |||
do wyznaczenia napięcia niezrównoważenia, gdyż <math>U_N = E_C</math>. W tej sytuacji poszczególne prądy fazowe są równe | |||
: <math>I_A={E_A-U_N \over Z_A}={400-400e^{j120^\circ} \over 40\sqrt{2}e^{j45^\circ}}=5\sqrt{2}e^{-j75^\circ}=1,8-j6,8</math> | |||
: <math>I_B={E_B-U_N \over Z_B}={400e^{-j120^\circ}-400e^{j120^\circ} \over 60e^{j90^\circ}}=-11,6</math> | |||
: <math>I_C=-I_A-I_B=9,8+j6,8</math> | |||
Po obliczeniu prądów na podstawie schematu zastępczego bez sprzężeń magnetycznych dla wyznaczenia napięć w układzie należy powrócić do obwodu ze sprzężeniami. Rzeczywiste napięcia na fazach odbiornika wynoszą | |||
: <math>U_A=RI_A+jX_LI_A+jX_{12}I_B+jX_{31}I_C=322+j263</math> | |||
: <math>U_B=jX_LI_B+jX_{12}I_A+jX_{23}I_C=-18-j335</math> | |||
: <math>U_C=jX_LI_C+jX_{31}I_A+jX_{23}I_B-jX_CI_C=-18</math> | |||
Zauważmy, że istnieje ogromna różnica między rzeczywistym napięciem <math>U_C</math> w fazie C, <math>U_C=-18</math>, a napięciem w tej samej fazie w obwodzie po likwidacji sprzężeń, <math>U_C=0</math>. Obwód po likwidacji sprzężeń jest równoważny obwodowi oryginalnemu jedynie pod względem prądowym. Napięcia na gałęziach zawierających cewki sprzężone nie odpowiadają ich odpowiednikom w obwodzie bez sprzężeń. | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:PEE_M6_Slajd21.png|500px]] | |||
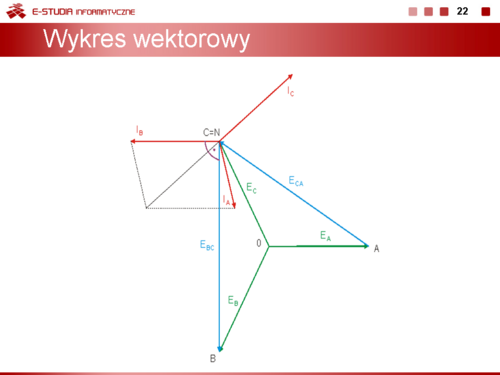
|valign="top"|Na rysunku obok i animacji poniżej przedstawiono wykres wektorowy prądów i napięć w obwodzie po likwidacji sprzężeń. | |||
[[Grafika:PEE_M6_rys6_15_animacja.gif]] | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:PEE_M6_Slajd22.png|500px]] | |||
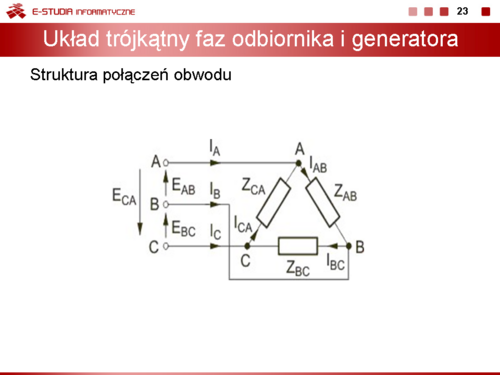
|valign="top"|'''Układ trójkątny faz odbiornika i generatora''' | |||
Schemat elektryczny połączeń elementów obwodu trójfazowego o odbiorniku i generatorze połączonych w trójkąt (układ trójkąt-trójkąt) przedstawia rysunku obok. | |||
|} | |} | ||
| Linia 47: | Linia 356: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika: | |valign="top" width="500px"|[[Grafika:PEE_M6_Slajd23.png|500px]] | ||
|valign="top"| | |valign="top"|Przyjmijmy dla uproszczenia, że impedancje przewodów zasilających poszczególne fazy są zerowe. Oznacza to, że napięcia na fazach odbiornika (włączonych międzyfazowo) są napięciami międzyfazowymi generatora, to jest | ||
: <math>U_{AB}=E_{AB}</math> | |||
: <math>U_{BC}=E_{BC}</math> | |||
: <math>U_{CA}=E_{CA}</math> | |||
Stąd przy zadanych wartościach impedancji odbiornika prądy fazowe tego odbiornika są określone wzorami | |||
: <math>I_{AB}=Y_{AB}E_{AB}</math> | |||
: <math>I_{BC}=Y_{BC}E_{BC}</math> | |||
: <math>I_{CA}=Y_{CA}E_{CA}</math> | |||
Prądy przewodowe zasilające obwód trójkątny odbiornika mogą być wyznaczone z zależności | |||
: <math>I_A=I_{AB}-I_{CA}</math> | |||
: <math>I_B=I_{BC}-I_{AB}</math> | |||
: <math>I_C=I_{CA}-I_{BC}</math> | |||
Zauważmy, że wobec powyższych wzorów suma prądów przewodowych w układzie, niezależnie od wartości impedancji odbiornika jest równa zeru | |||
: <math>I_A+I_B+I_C=0</math> | |||
|} | |} | ||
| Linia 54: | Linia 389: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika: | |valign="top" width="500px"|[[Grafika:PEE_M6_Slajd24.png|500px]] | ||
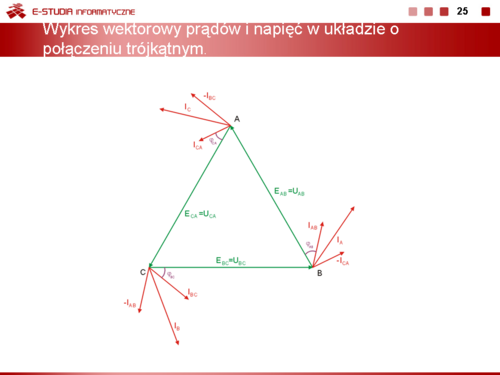
|valign="top"| | |valign="top"|Animacja poniżej oraz slajd obok przedstawiają wykres wektorowy prądów i napięć w układzie trójfazowym o połączeniu trójkątnym. | ||
[[Grafika:PEE_M6_anim_8.gif]] | |||
|} | |} | ||
| Linia 61: | Linia 398: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika: | |valign="top" width="500px"|[[Grafika:PEE_M6_Slajd24a.png|500px]] | ||
|valign="top"| | |valign="top"| | ||
W przypadku pełnej symetrii generatora i odbiornika wszystkie układy napięć i prądów w układzie będą również symetryczne a przesunięcia między prądami oraz napięciami poszczególnych faz w odpowiednich układach będą równe <math>120^\circ</math>. Interesująca jest wówczas relacja między prądami fazowymi oraz liniowymi układu. Z wykresu wektorowego przedstawionego na wcześniejszym rysunku widać, że w przypadku symetrycznym moduły wszystkich prądów liniowych są sobie równe, podobnie jak moduły wszystkich prądów fazowych przy równych przesunięciach fazowych między wektorami o kąt <math>120^\circ</math>. Z analizy przesunięć kątowych wynika, że kąt między wektorem prądu fazowego <math>I_f</math> oraz liniowego <math>I_l</math> jest równy <math>30^\circ</math>. Z zależności trygonometrycznych wynika, że | |||
: <math>{0,5|I_l| \over |I_f|}=cos30^\circ</math> | |||
skąd po prostych przekształceniach matematycznych otrzymuje się | |||
: <math>|I_l|=2|I_f|cos30^\circ=\sqrt{3}|I_f|</math> | |||
W układzie symetrycznym prąd liniowy jest <math>\sqrt{3}</math> razy większy niż prąd fazowy. Jest to identyczna relacja jaka istnieje między napięciami fazowymi i międzyfazowymi (liniowymi). | |||
|} | |} | ||
| Linia 68: | Linia 414: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika: | |valign="top" width="500px"|[[Grafika:PEE_M6_Slajd25.png|500px]] | ||
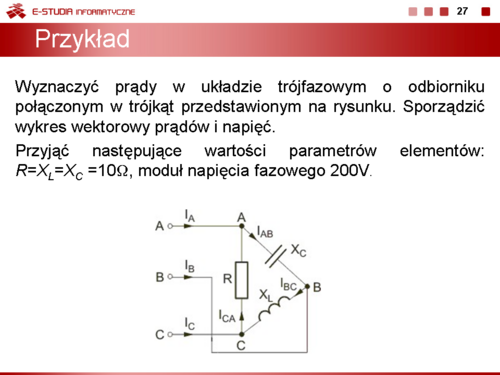
|valign="top"| | |valign="top"|Jako przykład wyznaczymy prądy w układzie trójfazowym o odbiorniku połączonym w trójkąt przedstawionym na rysunku obok (slajd 25). Należy również sporządzić wykres wektorowy prądów i napięć. Przyjąć następujące wartości parametrów elementów: <math>|E_f|=200V</math>, <math>R=X_L=X_C =10\Omega</math>. | ||
|} | |} | ||
| Linia 75: | Linia 422: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika: | |valign="top" width="500px"|[[Grafika:PEE_M6_Slajd26.png|500px]] | ||
|valign="top"| | |valign="top"|Napięcia międzyfazowe: | ||
: <math>|E_{mf}|=\sqrt{3}|E_f|</math> | |||
: <math>E_{AB}=200\sqrt{3}</math> | |||
: <math>E_{BC}=200\sqrt{3}e^{-j120^\circ}</math> | |||
: <math>E_{CA}=200\sqrt{3}e^{j120^\circ}</math> | |||
Prądy fazowe odbiornika: | |||
: <math>I_{AB}={E_{AB} \over -jX_C}=20\sqrt{3}e^{j90^\circ}</math> | |||
: <math>I_{BC}={E_{BC} \over jX_L}=20\sqrt{3}e^{-j210^\circ}</math> | |||
: <math>I_{CA}={E_{CA} \over R}=20\sqrt{3}e^{j120^\circ}</math> | |||
Prądy liniowe układu: | |||
: <math>I_A=I_{AB}-I_{CA}=17,32+j4,64</math> | |||
: <math>I_B=I_{BC}-I_{AB}=-30-j17,32</math> | |||
: <math>I_C=I_{CA}-I_{BC}=12,68+j12,68</math> | |||
|} | |} | ||
| Linia 82: | Linia 455: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika: | |valign="top" width="500px"|[[Grafika:PEE_M6_Slajd27.png|500px]] | ||
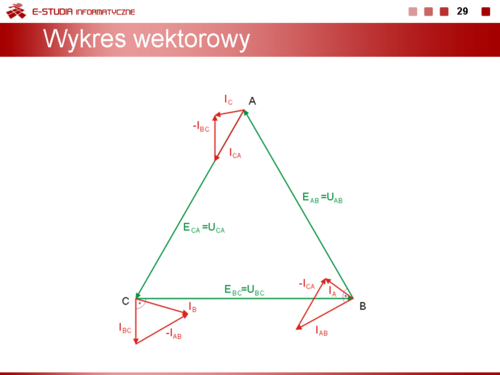
|valign="top"| | |valign="top"|Wykres wektorowy prądów i napięć przedstawiony jest na rysunku poniżej oraz na slajdzie obok. | ||
[[Grafika:PEE_M6_anim_9.gif ]] | |||
|} | |} | ||
| Linia 89: | Linia 465: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika: | |valign="top" width="500px"|[[Grafika:PEE_M6_Slajd28.png|500px]] | ||
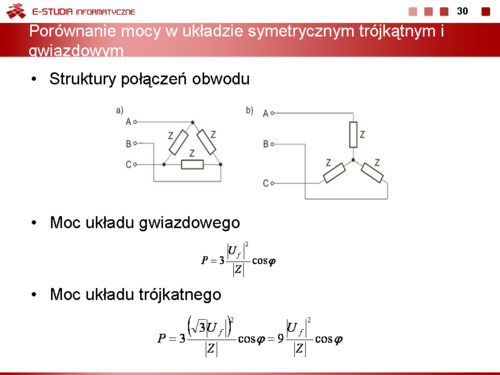
|valign="top"| | |valign="top"|Przełączenie impedancji odbiornika z połączenia trójkątnego w gwiazdowe powoduje zmianę mocy wydzielonej w odbiorniku. Załóżmy dla uproszczenia, że obwód trójfazowy jest symetryczny o impedancji fazy równej <math>Z\ </math>,. Schemat połączenia trójkątny i gwiazdowy impedancji przedstawiony jest na rysunku obok. | ||
Jak łatwo pokazać dla układu trójkątnego moc czynna <math>P\ </math>, układu jest równa | |||
: <math>P=3{(\sqrt{3}|U_f|)^2 \over |Z|}\cos \varphi = 9{|U_f|^2 \over |Z|}\cos \varphi</math> | |||
natomiast w układzie gwiazdowym wobec <math>U_N = 0</math> mamy | |||
: <math>P=3{|U_f|^2 \over |Z|}\cos \varphi</math> | |||
Jak wynika z powyższych wzorów przy przełączeniu odbiornika symetrycznego z gwiazdy na trójkąt pobór mocy czynnej wzrasta 3-krotnie. Przy tej samej wartości impedancji w obu połączeniach oznacza to <math>\sqrt{3}</math>-krotny wzrost prądu płynącego przez impedancję. | |||
|} | |} | ||
| Linia 96: | Linia 483: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"| | |valign="top" width="500px"|<applet code="dyplom.Applet1.class" archive="images/6/64/Dyplom.jar" width="640" height="480"> | ||
|valign="top"| | </applet> | ||
|valign="top"|Do obliczeń prądów, napięć i mocy w obwodach trójfazowych został opracowany program „Obwody trójfazowe” umieszczony obok. Pozwala on na symulację pracy układu trójfazowego o dowolnej strukturze połączeń. | |||
Centralne pole programu zajmuje schemat badanego obwodu (dostępne konfiguracje: gwiazda-gwiazda <math>Y-Y\ </math>,, gwiazda-trójkąt <math>Y-\Delta</math>, trójkąt-trójkąt <math>\;\Delta-\Delta\;</math> i trójkąt-gwiazda <math>\Delta-Y</math>), z symbolicznie zaznaczonym odbiornikiem i zasilaniem trójfazowym. | |||
Działanie programu rozpoczyna się po wybraniu odpowiedniej opcji obliczeń. Użytkownik może definiować własną strukturę obwodu (<math>\Delta\ </math>,,<math>Y\ </math>,, przewód zerowy), rodzaj i wartości parametrów odbiornika (R, L, C), wartości źródeł wymuszających, impedancję przewodu zerowego, format liczb zespolonych. | |||
W wyniku obliczeń otrzymuje się wartości prądów, napięć i mocy w obwodzie, jak również wykres wektorowy prądów i napięć oraz ich przebiegi czasowe. Program stanowi efektywne wirtualne laboratorium obwodów trójfazowych, umożliwiające studentowi samodzielne badanie zjawisk zachodzących w obwodach trójfazowych. | |||
|} | |} | ||
<hr width="100%"> | |||
'''Zadania sprawdzające''' | |||
''Zadanie 6.1'' | |||
Wyznaczyć prądy w obwodzie trójfazowym podanym na rysunku poniżej. Przyjąć następujące wartości parametrów elementów: <math>|E_f|=200V</math>, <math>Z_A=10\Omega</math>, <math>Z_B=(10-j10)\Omega</math>, <math>Z_C=(10+j10)\Omega</math>, <math>Z_N=50\Omega</math>. | |||
[[Grafika:PEE_M4_zadanie_6_1.png]] | |||
''Rozwiązanie'' | |||
Przyjmujemy następujące wartości symboliczne elementów: | |||
: <math>E_A=200</math> | |||
: <math>E_B=200e^{-j120^\circ}</math> | |||
: <math>E_C=200e^{j120^\circ}</math> | |||
: <math>Y_A={1 \over Z_A}=0,1</math> | |||
: <math>Y_B={1 \over Z_B}=0,05+j0,05</math> | |||
: <math>Y_C={1 \over Z_C}=0,05-j0,05</math> | |||
: <math>Y_N={1 \over Z_N}=0,02</math> | |||
Napięcie niezrównoważenia <math>U_N</math> | |||
: <math>U_N={E_AY_A+E_BY_B+E_CY_C \over Y_A+Y_B+Y_C+Y_N}=124,18</math> | |||
Prądy fazowe: | |||
: <math>I_A=(E_A-U_N)Y_A=7,58</math> | |||
: <math>I_B=(E_B-U_N)Y_B=-2,55-j19,87</math> | |||
: <math>I_C=(E_C-U_N)Y_C=2,55+j19,87</math> | |||
: <math>I_N=U_NY_N=2,48</math> | |||
Aktualna wersja na dzień 12:04, 5 wrz 2023

|

|
Przyjmijmy układ napięć fazowych generatora w następującej postaci
|
|
Na rysunku obok i animacji poniżej przedstawiono wykres wektorowy prądów i napięć w obwodzie po likwidacji sprzężeń. |
|
Animacja poniżej oraz slajd obok przedstawiają wykres wektorowy prądów i napięć w układzie trójfazowym o połączeniu trójkątnym. |

|
Napięcia międzyfazowe:
|
|
Wykres wektorowy prądów i napięć przedstawiony jest na rysunku poniżej oraz na slajdzie obok. |
| <applet code="dyplom.Applet1.class" archive="images/6/64/Dyplom.jar" width="640" height="480">
</applet> |
Do obliczeń prądów, napięć i mocy w obwodach trójfazowych został opracowany program „Obwody trójfazowe” umieszczony obok. Pozwala on na symulację pracy układu trójfazowego o dowolnej strukturze połączeń.
Centralne pole programu zajmuje schemat badanego obwodu (dostępne konfiguracje: gwiazda-gwiazda ,, gwiazda-trójkąt , trójkąt-trójkąt i trójkąt-gwiazda ), z symbolicznie zaznaczonym odbiornikiem i zasilaniem trójfazowym. Działanie programu rozpoczyna się po wybraniu odpowiedniej opcji obliczeń. Użytkownik może definiować własną strukturę obwodu (,,,, przewód zerowy), rodzaj i wartości parametrów odbiornika (R, L, C), wartości źródeł wymuszających, impedancję przewodu zerowego, format liczb zespolonych. W wyniku obliczeń otrzymuje się wartości prądów, napięć i mocy w obwodzie, jak również wykres wektorowy prądów i napięć oraz ich przebiegi czasowe. Program stanowi efektywne wirtualne laboratorium obwodów trójfazowych, umożliwiające studentowi samodzielne badanie zjawisk zachodzących w obwodach trójfazowych. |
Zadania sprawdzające
Zadanie 6.1
Wyznaczyć prądy w obwodzie trójfazowym podanym na rysunku poniżej. Przyjąć następujące wartości parametrów elementów: , , , , .
Rozwiązanie
Przyjmujemy następujące wartości symboliczne elementów:
Napięcie niezrównoważenia
Prądy fazowe: