PF Moduł 16: Różnice pomiędzy wersjami
mNie podano opisu zmian |
m Zastępowanie tekstu – „\</math>” na „\ </math>” |
||
| (Nie pokazano 5 pośrednich wersji utworzonych przez tego samego użytkownika) | |||
| Linia 31: | Linia 31: | ||
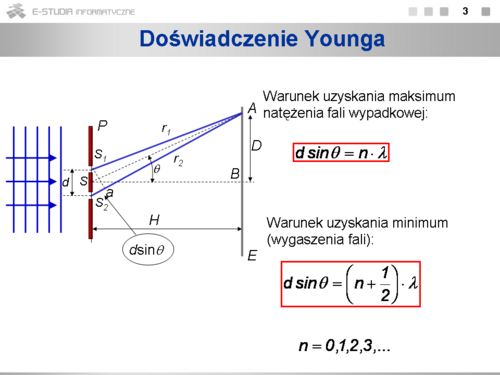
Zjawisko interferencji dla fal świetlnych zostało po raz pierwszy zaobserwowane i zinterpretowane jako przejaw falowej natury światła przez Thomasa Younga w 1801 roku. | Zjawisko interferencji dla fal świetlnych zostało po raz pierwszy zaobserwowane i zinterpretowane jako przejaw falowej natury światła przez Thomasa Younga w 1801 roku. | ||
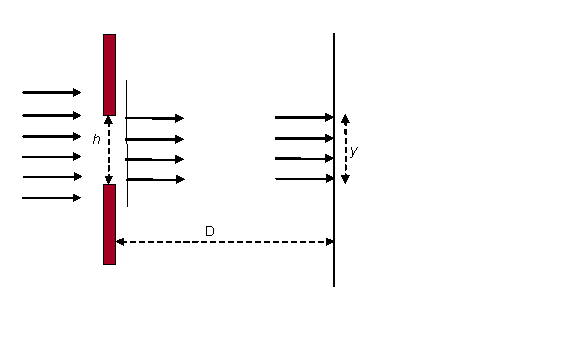
Uproszczony schemat doświadczenia Younga przedstawia rysunek. Światło w postaci fali płaskiej pada na układ dwóch szczelin <math>S_1\ | Uproszczony schemat doświadczenia Younga przedstawia rysunek. Światło w postaci fali płaskiej pada na układ dwóch szczelin <math>S_1\ </math>, i <math>S_2\ </math>, w przesłonie <math>P\ </math>,. Interesuje nas rezultat nałożenia się fal w punkcie <math>A\ </math>, na ekranie <math>E\ </math>, ustawionym za szczelinami. Światło padające symbolizują równoległe niebieskie linie (powierzchnie falowe) i strzałki (promienie) z lewej strony. Promienie świetlne, które przeszły przez szczeliny <math>S_1\ </math>, i <math>S_2\ </math>, docierają do punktu <math>A\ </math>,, ale drogi ich <math>r_1\ </math>, i <math>r_2\ </math>, nie są takie same. Jeśli więc faza fali świetlnej była w płaszczyźnie szczelin taka sama, to w punkcie <math>A\ </math>, będzie różna wskutek różnicy dróg. Warunek wzmocnienia lub wygaszenia wynika z geometrycznych zależności zilustrowanych na rysunku. Trzeba tu zwrócić uwagę, że w rzeczywistości odległość ekranu od przesłony jest o wiele większa niż odległość pomiędzy szczelinami tzn. <math>H>>d</math> . W takim przypadku promienie <math>r_1\ </math>, i <math>r_2\ </math>, są z dobrym przybliżeniem równoległe, a trójkąty <math>SBA\ </math>, i <math>S_1aS_2\ </math>, możemy uznać za podobne, co z kolei oznacza, że kąty <math>ASB\ </math>, i <math>S_2S_1a\ </math>, są sobie równe. Kąt <math>ASB\ </math>,, który może być łatwo zmierzony, oznaczyliśmy symbolem <math>\theta\ </math>,. Różnica dróg promieni od szczelin do punktu <math>A\ </math>, równa jest <math>d sin\theta\ </math>,. Jeśli różnica ta będzie równa całkowitej wielokrotności długości fali, to nastąpi wzmocnienie, jeśli równa będzie równa nieparzystej wielokrotności połowy długości fali - nastąpi wygaszenie. Warunek uzyskania maksimum natężenia fali wypadkowej zapiszemy w postaci: <math>d sin\theta=n\lambda</math> , warunek uzyskania minimum, czyli wygaszenia: | ||
: <math> | : <math>d sin\theta=\left(2n+1\right) \frac{\lambda}{2}=\left(n+\frac{1}{2}\right)\lambda</math> | ||
|} | |} | ||
| Linia 49: | Linia 49: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="450px" valign="top"|[[Grafika:PF_M16_Slajd5.png]] | |width="450px" valign="top"|[[Grafika:PF_M16_Slajd5.png]] | ||
|valign="top"|Uogólnijmy nasze rozważania. Rozpatrzmy dwie fale o tych samych amplitudach i częstościach, ale różniące się fazą: <math> | |valign="top"|Uogólnijmy nasze rozważania. Rozpatrzmy dwie fale o tych samych amplitudach i częstościach, ale różniące się fazą: <math>y_1=y_0 sin(kx-\omega t)</math> oraz <math>y_1=y_0 sin(kx-\omega t-\varphi)</math>. Jak wspominaliśmy już, w przypadku fal elektromagnetycznych, jako zaburzenie y traktujemy zazwyczaj wartość wektora natężenia pola elektrycznego. | ||
Zgodnie z zasadą superpozycji fal, zaburzenie wypadkowe w danym punkcie przestrzeni i momencie czasu będzie sumą zaburzeń pochodzących od obu fal <math> | Zgodnie z zasadą superpozycji fal, zaburzenie wypadkowe w danym punkcie przestrzeni i momencie czasu będzie sumą zaburzeń pochodzących od obu fal <math>y_{12}=y_1+y_2</math>. Po zastosowaniu trygonometrycznego wzoru na sumę sinusów, otrzymujemy: | ||
: <math> | : <math>y_{12}=y_0 \left [2sin(kx-\omega t -\varphi)cos{\frac{\varphi}{2}} \right]</math> | ||
|} | |} | ||
| Linia 61: | Linia 61: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="450px" valign="top"|[[Grafika:PF_M16_Slajd6.png]] | |width="450px" valign="top"|[[Grafika:PF_M16_Slajd6.png]] | ||
|valign="top"|We wzorze na <math>y_{12}\ | |valign="top"|We wzorze na <math>y_{12}\ </math>, możemy wyodrębnić czynnik niezależny od czasu i położenia. Jest to amplituda równa <math>2y_0 cos{\frac{\varphi}{2}}\ </math>,. Amplituda ta zależy od <math>\varphi\ </math>,, czyli różnicy faz pomiędzy falami. Maksymalna amplituda równa będzie podwojonej amplitudzie fal składowych, co nastąpi, kiedy różnica faz będzie równa zeru. Amplituda równa zeru będzie dla różnicy faz równej <math>\pi\ </math>,, wtedy przeciwne w fazie zaburzenia będą się wzajemnie znosić. Dla innych różnic faz amplituda będzie przyjmować wartości pośrednie. | ||
|} | |} | ||
| Linia 79: | Linia 79: | ||
|valign="top"|Na zakończenie dwie uwagi: | |valign="top"|Na zakończenie dwie uwagi: | ||
#W praktyce, dla spełnienia zarówno warunków równoległości promieni jak i skończonej odległości <math>H\ | #W praktyce, dla spełnienia zarówno warunków równoległości promieni jak i skończonej odległości <math>H\ </math>, pomiędzy przesłoną i ekranem, stosuje się zwykle soczewkę skupiającą równoległe promienie w płaszczyźnie ogniskowej, gdzie umieszcza się ekran; | ||
#Założyliśmy tu milcząco, że szerokość szczeliny jest zaniedbywanie mała w stosunku do odległości pomiędzy szczelinami. | #Założyliśmy tu milcząco, że szerokość szczeliny jest zaniedbywanie mała w stosunku do odległości pomiędzy szczelinami. | ||
| Linia 92: | Linia 92: | ||
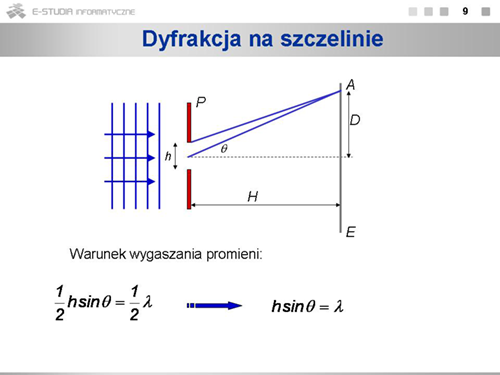
|valign="top"|Czy możliwa jest interferencja światła przechodzącego przez pojedynczą szczelinę lub otwór? Odruchowa odpowiedź jest - że nie, bo przechodzące światło nie ma z czym interferować. Zasada Hyghensa mówi jednak, że każdy punkt, do którego dochodzi fala staje się źródłem nowej fali kulistej. Fale pochodzące z różnych punktów szczeliny mogą więc także interferować. Kiedy szczelina jest bardzo szeroka, to w rezultacie tworzy się czoło fali płaskiej i efektu interferencji nie obserwujemy. Kiedy jednak rozmiary szczeliny stają się porównywalne z długością fali, efekt interferencji powinien być możliwy do zaobserwowania. Rzeczywiście, efekty takie się obserwuje i choć w swej naturze nie różnią się one od znanej nam już interferencji otrzymały inną nazwę - '''dyfrakcji''', czyli "uginania się" fal. | |valign="top"|Czy możliwa jest interferencja światła przechodzącego przez pojedynczą szczelinę lub otwór? Odruchowa odpowiedź jest - że nie, bo przechodzące światło nie ma z czym interferować. Zasada Hyghensa mówi jednak, że każdy punkt, do którego dochodzi fala staje się źródłem nowej fali kulistej. Fale pochodzące z różnych punktów szczeliny mogą więc także interferować. Kiedy szczelina jest bardzo szeroka, to w rezultacie tworzy się czoło fali płaskiej i efektu interferencji nie obserwujemy. Kiedy jednak rozmiary szczeliny stają się porównywalne z długością fali, efekt interferencji powinien być możliwy do zaobserwowania. Rzeczywiście, efekty takie się obserwuje i choć w swej naturze nie różnią się one od znanej nam już interferencji otrzymały inną nazwę - '''dyfrakcji''', czyli "uginania się" fal. | ||
Na rysunku pokazano dwa przykładowe promienie, które będą z sobą interferować. Szerokość szczeliny oznaczamy symbolem <math>h\ | Na rysunku pokazano dwa przykładowe promienie, które będą z sobą interferować. Szerokość szczeliny oznaczamy symbolem <math>h\ </math>,. Podobnie jak poprzednio, zakładamy, że <math>H>>h\ </math>, i możemy uznać promienie biegnące z różnych punktów szczeliny za równoległe, co jest na ogół z niezłym przybliżeniem spełnione i upraszcza opis ilościowy. Taki przypadek nosi nazwę dyfrakcji Fraunhofera w odróżnieniu od dyfrakcji Fresnela, gdzie zakłada się, że odległość pomiędzy źródłem i ekranem ma skończoną wartość. Rozważmy na początek dwa promienie wybiegające z punktów szczeliny odległych o <math>h/2\ </math>,. Warunek ich wygaszania się <math>\frac{h}{2}sin\theta=\left(n+\frac{1}{2} \right)\lambda</math> dla n=0 (pierwsze minimum) wyraża się wzorem: | ||
: <math> | : <math>\frac{h}{2}sin\theta=\frac{1}{2}\lambda</math> | ||
|} | |} | ||
| Linia 113: | Linia 113: | ||
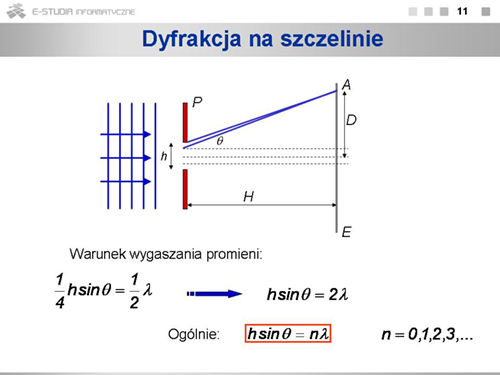
: <math> | : <math>\frac{1}{4}h sin\theta=\frac{1}{2}\lambda</math> , czyli <math>h sin\theta=2\lambda</math> | ||
| Linia 119: | Linia 119: | ||
: <math> | : <math>h sin\theta=n\lambda</math> , gdzie <math>n=1, 2, 3,...\ </math>, | ||
| Linia 130: | Linia 130: | ||
|valign="top"|Minimów i leżących pomiędzy nimi maksimów może więc być bardzo wiele. Powstaje pytanie, jaki będzie rozkład natężeń w obrazie dyfrakcyjnym, jak natężenie wypadkowej fali zależeć będzie od kąta odchylenia promieni od pierwotnego kierunku? Największe wzmocnienie natężenia fali uzyskujemy, gdy obie fale mają taką sama fazę, największe osłabienie, gdy faza jest przeciwna. Pomiędzy tymi skrajnymi przypadkami mamy wszystkie przypadki pośrednie, zależne od różnicy faz. | |valign="top"|Minimów i leżących pomiędzy nimi maksimów może więc być bardzo wiele. Powstaje pytanie, jaki będzie rozkład natężeń w obrazie dyfrakcyjnym, jak natężenie wypadkowej fali zależeć będzie od kąta odchylenia promieni od pierwotnego kierunku? Największe wzmocnienie natężenia fali uzyskujemy, gdy obie fale mają taką sama fazę, największe osłabienie, gdy faza jest przeciwna. Pomiędzy tymi skrajnymi przypadkami mamy wszystkie przypadki pośrednie, zależne od różnicy faz. | ||
Podzielmy w myśli całą szerokość szczeliny na n pasków. Ilustruje to rysunek obok, gdzie <math>n=5\ | Podzielmy w myśli całą szerokość szczeliny na n pasków. Ilustruje to rysunek obok, gdzie <math>n=5\ </math>,. (Wskaźnik <math>n\ </math>, odgrywa tu pomocniczą rolę i nie należy go mylić ani ze współczynnikiem załamania, ani z numeracją maksimów i minimów interferencyjnych.) Różnica faz <math>\Delta \varphi\ </math>, dla fal biegnących od dwóch sąsiednich pasków zależy od różnicy dróg <math>\Delta r</math>, jak pokazano na rysunku. Kiedy różnica dróg równa jest długości fali, to odpowiadająca różnica faz równa jest <math>2\pi\ </math>,. | ||
Mamy więc proporcję: | Mamy więc proporcję: | ||
<math> | <math>\frac{\Delta r}{\lambda}=\frac{\Delta \varphi}{2\pi}</math> czyli <math>\Delta \varphi=\frac{2\pi}{\lambda}\Delta r=\frac{2\pi}{\lambda}\Delta h sin\theta</math> | ||
gdzie <math>\Delta h\ | gdzie <math>\Delta h\ </math>, jest odległością pomiędzy punktami w płaszczyźnie przesłony, to jest szerokością myślowo wyodrębnionego jednego paska. Otrzymaliśmy wzór na różnicę fazy między falami pochodzącymi od kolejnych części szczeliny. Musimy teraz dodać wszystkie fale, aby znaleźć falę wypadkową, czyli jej amplitudę i fazę. | ||
|} | |} | ||
| Linia 146: | Linia 146: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="450px" valign="top"|[[Grafika:PF_M16_Slajd13.png]] | |width="450px" valign="top"|[[Grafika:PF_M16_Slajd13.png]] | ||
|valign="top"|Dla wyznaczenia sumarycznej fazy oraz amplitudy wypadkowej fali wykorzystamy tu metodę tak zwanych strzałek fazowych. Metoda ta umożliwia graficzne dodawanie wielkiej liczby fal o tej samej amplitudzie <math>E_0\ | |valign="top"|Dla wyznaczenia sumarycznej fazy oraz amplitudy wypadkowej fali wykorzystamy tu metodę tak zwanych strzałek fazowych. Metoda ta umożliwia graficzne dodawanie wielkiej liczby fal o tej samej amplitudzie <math>E_0\ </math>, i częstości <math>\omega\ </math>,, a różniących się fazą. Ilustruje to rysunek. Niech pierwsza fala wynosi <math>E_1=E_0 sin(\omega t)</math> , kolejna - różniąca się od pierwszej przesunięciem w fazie o <math>\varphi\ </math>, będzie <math>E_2=E_0 sin(\omega t+\varphi)</math>, kolejna niech będzie przesunięta o <math>2\varphi\ </math>, itd. Każda strzałka reprezentuje falę o danej amplitudzie, której odpowiada długość strzałki. Faza fali określona jest przez kąt między osią x a kierunkiem strzałki. Wypadkową amplitudę i fazę otrzymujemy sumując wektorowo strzałki (kolejna strzałka ma swój początek w miejscu, gdzie kończy się poprzednia). Na rysunku pokazane są przykładowo różnymi kolorami cztery fale i ich złożenie pokazane kolorem czerwonym. | ||
|} | |} | ||
| Linia 154: | Linia 154: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="450px" valign="top"|[[Grafika:PF_M16_Slajd14.png]] | |width="450px" valign="top"|[[Grafika:PF_M16_Slajd14.png]] | ||
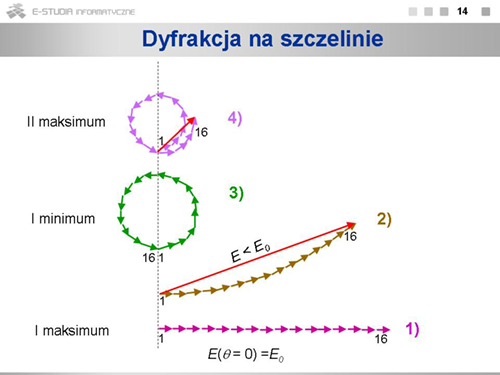
|valign="top"|W naszym przypadku fali przechodzącej przez szczelinę, sumaryczna amplituda i sumaryczna faza będzie złożeniem n składowych i zależeć będzie, zgodnie ze wzorem <math> | |valign="top"|W naszym przypadku fali przechodzącej przez szczelinę, sumaryczna amplituda i sumaryczna faza będzie złożeniem n składowych i zależeć będzie, zgodnie ze wzorem <math>\Delta \varphi=\frac{2\pi}{\lambda}\Delta h sin\theta</math> od kąta <math>\theta\ </math>, określającego położenie danego punktu na ekranie względem szczeliny. | ||
Jeśli kąt ten jest równy zeru, czyli punkt obserwacji leży na wprost szczeliny, to i <math>\Delta \varphi</math> będzie równe zeru i sumaryczna amplituda będzie algebraiczną sumą <math>n\ | Jeśli kąt ten jest równy zeru, czyli punkt obserwacji leży na wprost szczeliny, to i <math>\Delta \varphi</math> będzie równe zeru i sumaryczna amplituda będzie algebraiczną sumą <math>n\ </math>, jednakowych składników. Jeśli kąt <math>\theta\ </math>, będzie inny, musimy sumować <math>n\ </math>, fal składowych zgodnie z metodą strzałek fazowych. Ilustruje to rysunek, gdzie <math>n=16\ </math>,. Przypadek 1) odpowiada sytuacji, gdy <math>\theta=0</math>, a więc i różnica faz <math>\Delta \varphi=0</math>. Sumaryczna amplituda jest tu maksymalna, oznaczyliśmy ją <math>E_0\ </math>,. Kolejne przypadki 2), 3) i 4) odpowiadają wzrastającej wartości kąta obserwacji <math>\theta\ </math>,. Przypadek 2) ilustruje sytuację, gdy <math>\theta\ </math>, nieco większe od zera. Suma algebraiczna wszystkich 16 składników (długość łuku) jest taka sama, jak poprzednio, równa <math>E_0\ </math>,, ale wypadkowa amplituda (wartość sumy wektorowej) jest mniejsza od <math>E_0\ </math>,. W przypadku 3) sumaryczna amplituda wynosi zero, czyli będzie to pierwsze minimum. Przy dalszym wzroście kąta <math>\theta\ </math>, amplituda znów będzie różna od zera, ale jej wartość stanie się o wiele mniejsza. Liczba pasków, na które podzieliliśmy w myśli szczelinę może być dowolna. Im będzie większa, tym węższe będą paski, ale końcowe przesunięcie fazowe i zmiana amplitudy będą, dla danej długości fali, określone tylko wartością kąta odchylenia <math>\theta\ </math>,. (Pomocniczy wskaźnik <math>n\ </math>, przestaje więc być istotny i dalej potrzebny.) Związek pomiędzy wartością kąta <math>\theta\ </math>,, a amplitudą wypadkowej fali możemy znaleźć rozpatrując zależności geometryczne zilustrowane na rysunku. | ||
|} | |} | ||
| Linia 164: | Linia 164: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="450px" valign="top"|[[Grafika:PF_M16_Slajd15.png]] | |width="450px" valign="top"|[[Grafika:PF_M16_Slajd15.png]] | ||
|valign="top"|Kiedy liczba pasków będzie zmierzać do nieskończoności, a ich szerokość do zera, to łuk strzałek fazowych będzie można przybliżyć łukiem okręgu. Długość łuku jest równa <math>E_0\ | |valign="top"|Kiedy liczba pasków będzie zmierzać do nieskończoności, a ich szerokość do zera, to łuk strzałek fazowych będzie można przybliżyć łukiem okręgu. Długość łuku jest równa <math>E_0\ </math>,, a kąt <math>\varphi\ </math>, pomiędzy stycznymi do łuku na obu jego końcach równy jest różnicy faz pomiędzy promieniami biegnącymi z obu krańców szczeliny. Kąt ten, mierzony w radianach, równy jest z definicji stosunkowi długości łuku, czyli <math>E_0\ </math>,, do promienia <math>R\ </math>, to znaczy <math>\varphi=E_0/R\ </math>,. Z kolei, jak widać na rysunku, wypadkowa amplituda fali obserwowanej pod kątem <math>\theta\ </math>, wynosi <math>E_{\theta}=2Rsin\alpha</math> , zaś <math>\alpha=\varphi/2</math> . Wynika z tego, że <math>E_{\theta}=E_0 \frac{sin\alpha}{\alpha}</math>. | ||
Wypadkowa różnica faz odpowiada promieniom biegnącym z dwóch krańców szczeliny i określona jest tak samo, jak różnica faz dla dwóch sąsiednich pasków, jeśli szerokość paska zamienimy szerokością szczeliny: <math> | Wypadkowa różnica faz odpowiada promieniom biegnącym z dwóch krańców szczeliny i określona jest tak samo, jak różnica faz dla dwóch sąsiednich pasków, jeśli szerokość paska zamienimy szerokością szczeliny: <math>\varphi=\frac{2\pi}{\lambda}h sin\theta=2\alpha</math> , czyli <math>\alpha=\frac{\pi}{\lambda}h sin\theta</math> . | ||
W ten sposób różnica faz <math>\varphi\ | W ten sposób różnica faz <math>\varphi\ </math>, określona została przez mierzalne wielkości: szerokość szczeliny <math>h\ </math>,, długość fali <math>\lambda\ </math>, i kąt obserwacji <math>\theta\ </math>,. Podstawiając wyznaczoną wypadkową różnicę faz do wzoru <math>E_{\theta}=E_0 \frac{sin\alpha}{\alpha}</math> , otrzymujemy wyrażenie na amplitudę fali wypadkowej. Intensywność obrazu dyfrakcyjnego proporcjonalna jest do kwadratu amplitudy. Zapiszmy więc kompletny wzór na rozkład intensywności obrazu dyfrakcyjnego zależny jedynie od mierzalnych wielkości, czyli umożliwiający weryfikację doświadczalną. Przez <math>I_{wzgl}\ </math>, oznaczamy względną intensywność określoną jako stosunek intensywności dla danego kąta do intensywności maksymalnej, czyli dla kąta <math>\theta\ </math>, równego zeru. | ||
<math> | <math>I_{\theta}=I_0 \left(\frac{sin\alpha}{\alpha} \right)^2</math> , lub <math>I_{wzgl}=\frac{I_{\theta}}{I_0} =\left(\frac{sin\alpha}{\alpha} \right)^2</math> , gdzie <math>\alpha=\pi \left(\frac{h}{\lambda} \right)sin\theta</math> | ||
|} | |} | ||
| Linia 178: | Linia 178: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="450px" valign="top"|[[Grafika:PF_M16_Slajd16.png]] | |width="450px" valign="top"|[[Grafika:PF_M16_Slajd16.png]] | ||
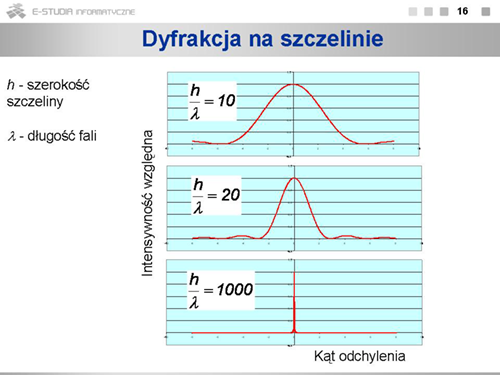
|valign="top"|Warto zobaczyć, jak zmiana intensywności zależy od szerokości szczeliny i długości fali. Z postaci wzoru na <math>I_{wzgl}\ | |valign="top"|Warto zobaczyć, jak zmiana intensywności zależy od szerokości szczeliny i długości fali. Z postaci wzoru na <math>I_{wzgl}\ </math>, widać, że zależy nie tyle od samych tych wartości, ale od ich stosunku <math>h/{\lambda}\ </math>, . Szerokość głównego maksimum dyfrakcyjnego jest tym większa, im węższa jest szczelina. Gdy szerokość szczeliny jest dużo większa od długości fali (dolny wykres) zjawiska dyfrakcji, czyli ugięcia na szczelinie, praktycznie nie obserwujemy. | ||
|} | |} | ||
| Linia 188: | Linia 188: | ||
|valign="top"|'''Złożenie interferencji i dyfrakcji''' | |valign="top"|'''Złożenie interferencji i dyfrakcji''' | ||
Uzyskaliśmy interferencyjne efekty na pojedynczej szczelinie, zaś poprzednio rozważaliśmy układ dwóch szczelin, gdzie również określiliśmy warunki na wzmacnianie i wygaszanie wypadkowej fali interferencyjnej. Można się więc spodziewać, że w układzie dwóch szczelin, uzyskamy superpozycje obu dyskutowanych tu efektów. Przypomnijmy sobie wzór na falę, będącą rezultatem nałożenia się dwóch fal o tych samych częstościach i amplitudach. Uzyskujemy fale wypadkową, <math>y_{12}\ | Uzyskaliśmy interferencyjne efekty na pojedynczej szczelinie, zaś poprzednio rozważaliśmy układ dwóch szczelin, gdzie również określiliśmy warunki na wzmacnianie i wygaszanie wypadkowej fali interferencyjnej. Można się więc spodziewać, że w układzie dwóch szczelin, uzyskamy superpozycje obu dyskutowanych tu efektów. Przypomnijmy sobie wzór na falę, będącą rezultatem nałożenia się dwóch fal o tych samych częstościach i amplitudach. Uzyskujemy fale wypadkową, <math>y_{12}\ </math>,, której amplituda zależy od różnicy faz fal składowych. W naszym przypadku możemy wzór na amplitudę zapisać następująco: | ||
: <math> | : <math>E_i=2E_{0i}cos \left(\frac{\varphi_i}{2} \right)=E_m cos\alpha_i</math> | ||
gdzie przez <math>E_i\ | gdzie przez <math>E_i\ </math>, (i – od interferencji) oznaczyliśmy amplitudę fali zależną od różnicy faz promieni przechodzących przez dwie szczeliny, a przez <math>E_{0i}\ </math>, amplitudę fali biegnącej z każdej szczeliny. Amplituda maksymalna <math>E_m\ </math>, jest sumą obu amplitud składowych <math>E_m=2E_{0i}</math>. Podobnie jak w przypadku dyfrakcji <math>\alpha_i=\varphi_i /2</math>. Należy jeszcze powiązać różnicę faz z kątem odchylenia promieni od pierwotnego kierunku fali padającej na układ szczelin. Wykorzystamy tu otrzymaną dla pojedynczej szczeliny zależność <math>\alpha=\frac{\pi}{\lambda}h sin\theta</math> , gdzie zamiast szerokości szczeliny h wstawiamy odległość pomiędzy dwoma szczelinami <math>d\ </math>, : <math>\alpha_i \frac{\pi d}{\lambda} sin\theta</math>. | ||
Natężenie fali (intensywność) jest proporcjonalna do kwadratu amplitudy. Intensywność obrazu interferencyjnego możemy więc zapisać w postaci: | Natężenie fali (intensywność) jest proporcjonalna do kwadratu amplitudy. Intensywność obrazu interferencyjnego możemy więc zapisać w postaci: | ||
: <math> | : <math>I_i=I_{mi}cos^2 \alpha_i</math> | ||
gdzie <math>I_{mi}\ | gdzie <math>I_{mi}\ </math>, jest maksymalną intensywnością promieni biegnących z każdej szczeliny. | ||
|} | |} | ||
| Linia 211: | Linia 211: | ||
|valign="top"|Ta maksymalna intensywność zależna jest jednak od efektów dyfrakcyjnych <math>I_{mi}=I_0 \left(\frac{sin\alpha}{\alpha} \right)^2</math>. Intensywność łączna zawierająca w sobie oba efekty wyrazi się więc wzorem: | |valign="top"|Ta maksymalna intensywność zależna jest jednak od efektów dyfrakcyjnych <math>I_{mi}=I_0 \left(\frac{sin\alpha}{\alpha} \right)^2</math>. Intensywność łączna zawierająca w sobie oba efekty wyrazi się więc wzorem: | ||
<math> | <math>I_{\theta_{id}}=I_m (cos\alpha_i)^2\cdot \left(\frac{sin\alpha_d}{\alpha_d} \right)^2</math> , gdzie <math>\alpha_i= \frac{\pi d}{\lambda} sin\theta</math> , <math>\alpha_d= \frac{\pi h}{\lambda} sin\theta</math> | ||
Jest to końcowy wzór zależny wyłącznie od wielkości mierzalnych. Indeksami "i" i "d" oznaczyliśmy kąty odpowiadające interferencji i dyfrakcji. Symbolem d oznaczona jest odległość pomiędzy szczelinami, a symbolem h, szerokość każdej ze szczelin. <math>I_m\ | Jest to końcowy wzór zależny wyłącznie od wielkości mierzalnych. Indeksami "i" i "d" oznaczyliśmy kąty odpowiadające interferencji i dyfrakcji. Symbolem d oznaczona jest odległość pomiędzy szczelinami, a symbolem h, szerokość każdej ze szczelin. <math>I_m\ </math>, jest maksymalną intensywnością odpowiadającą promieniom biegnącym na wprost. | ||
|} | |} | ||
| Linia 229: | Linia 229: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="450px" valign="top"|[[Grafika:PF_M16_Slajd20.png]] | |width="450px" valign="top"|[[Grafika:PF_M16_Slajd20.png]] | ||
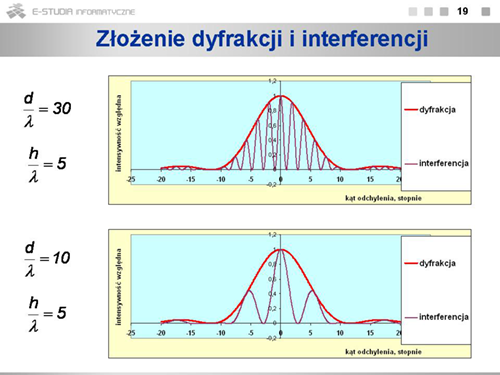
|valign="top"|Szerokość szczelin <math>h\ | |valign="top"|Szerokość szczelin <math>h\ </math>, wpływa natomiast na zależność intensywności linii od kąta odchylenia <math>\theta\ </math>,. Dla szerokich szczelin intensywność szybko maleje wraz z kątem <math>\theta\ </math>,, dla szczelin wąskich możemy obserwować stosunkowo silne linie przy dużych kątach odchylenia. | ||
|} | |} | ||
| Linia 239: | Linia 239: | ||
|valign="top"|'''Siatka dyfrakcyjna''' | |valign="top"|'''Siatka dyfrakcyjna''' | ||
Siatką dyfrakcyjną nazywamy układ wielu szczelin. Charakteryzuje ją wielkość zwana stałą siatki <math>d\ | Siatką dyfrakcyjną nazywamy układ wielu szczelin. Charakteryzuje ją wielkość zwana stałą siatki <math>d\ </math>,, która równa jest odległości pomiędzy dwiema sąsiednimi szczelinami, szerokość szczeliny <math>h\ </math>, oraz liczba szczelin <math>N\ </math>,. Oczekujemy, że w przypadku siatki dyfrakcyjnej efekt interferencyjny będzie silniejszy, bo sumować się będą składniki pochodzące od każdej pary sąsiednich szczelin. Wystąpią też efekty dodatkowe związane z interferencją pomiędzy innymi kombinacjami dwóch szczelin w siatce. Warunek wzmocnienia dla par sąsiednich szczelin będzie taki sam jak dla układu dwóch szczelin, czyli kąt odchylenia określony będzie stosunkiem długości fali padającej do stałej siatki. Podobnie jak w przypadku dwóch szczelin o określonych szerokościach wystąpią też efekty dyfrakcyjne zależne od szerokości samych szczelin <math>h\ </math>,. Zapiszmy więc warunek wzmocnienia w postaci: <math>sin\theta=n\frac{\lambda}{d}</math> , gdzie <math>n=1, 2, 3,...\ </math>, | ||
Wielkość <math>n\ | Wielkość <math>n\ </math>, nazywamy rzędem widma. | ||
|} | |} | ||
| Linia 249: | Linia 249: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="450px" valign="top"|[[Grafika:PF_M16_Slajd22.png]] | |width="450px" valign="top"|[[Grafika:PF_M16_Slajd22.png]] | ||
|valign="top"|Dla znalezienia warunków określających położenia minimów postąpimy analogicznie do znajdowania minimów dyfrakcyjnych w pojedynczej szczelinie. Znajdziemy warunek wygaszania się promieni z pierwszej i drugiej części siatki, odległych od siebie o <math>Nd/2\ | |valign="top"|Dla znalezienia warunków określających położenia minimów postąpimy analogicznie do znajdowania minimów dyfrakcyjnych w pojedynczej szczelinie. Znajdziemy warunek wygaszania się promieni z pierwszej i drugiej części siatki, odległych od siebie o <math>Nd/2\ </math>, . Jeśli rozpatrujemy promienie odchylone względem pierwotnego kierunku o kąt <math>\theta\ </math>,, to ich różnica dróg <math>\Delta r\ </math>, wynosić będzie: | ||
: <math> | : <math>\Delta r=\frac{Nd}{2}sin\theta</math> | ||
Pierwsze wygaszenie nastąpi, kiedy ta różnica równa będzie połowie długości fali, czyli kiedy | Pierwsze wygaszenie nastąpi, kiedy ta różnica równa będzie połowie długości fali, czyli kiedy | ||
:<math> | :<math>\frac{Nd}{2}sin\theta_1=\frac{\lambda}{2}</math> ,a więc <math>sin\theta_1=\frac{\lambda}{Nd}</math> | ||
Kolejne minima dane będą zależnością: | Kolejne minima dane będą zależnością: | ||
:<math> | :<math>sin\theta_i=i\cdot \frac{\lambda}{Nd}</math> , gdzie <math>i=1, 2, 3,...\ </math>, | ||
Kiedy jednak i stanie się równe <math>N\ | Kiedy jednak i stanie się równe <math>N\ </math>, to zamiast minimum, spełniony zostanie warunek na pierwsze boczne maksimum. | ||
Uzyskaliśmy bardzo ciekawy rezultat. Główne maksima, dla których jest spełniony warunek <math> | Uzyskaliśmy bardzo ciekawy rezultat. Główne maksima, dla których jest spełniony warunek <math>sin\theta=n \frac{\lambda}{d}</math> , oddzielone będą szeregiem minimów rozdzielających wtórne maksima o wiele słabsze od głównych. Im więcej będzie szczelin, tym więcej będzie minimów, w rezultacie tym węższe będą maksima główne. Dla określonych długości fal uzyskamy silne i wąskie linie widmowe. | ||
|} | |} | ||
| Linia 271: | Linia 271: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="450px" valign="top"|[[Grafika:PF_M16_Slajd23.png]] | |width="450px" valign="top"|[[Grafika:PF_M16_Slajd23.png]] | ||
|valign="top"|Na ilustracji górnej, dla liczby szczelin <math>N=4\ | |valign="top"|Na ilustracji górnej, dla liczby szczelin <math>N=4\ </math>,, widzimy maksima główne o dużej intensywności i znacznie słabsze maksima wtórne. Już dla <math>N=20\ </math>,, dolna ilustracja, maksima wtórne stają się praktycznie niewidoczne, a maksima główne to wąskie linie. Zauważmy, że typowa siatka dyfrakcyjna zawiera tysiące szczelin tak, że obraz z niej uzyskany to praktycznie tylko maksima główne występujące jako wąskie linie. | ||
|} | |} | ||
| Linia 279: | Linia 279: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="450px" valign="top"|[[Grafika:PF_M16_Slajd24.png]] | |width="450px" valign="top"|[[Grafika:PF_M16_Slajd24.png]] | ||
|valign="top"|Na zdjęciu pokazane są prążki interferencyjne uzyskane na ekranie za siatką dyfrakcyjną oświetloną światłem lampy sodowej. Lampa taka emituje żółte światło monochromatyczne o długości fali 589,3 nm. Widzimy najmocniejszy prążek rzędu zerowego, obserwowany pod kątem <math>\theta=0^\circ\ | |valign="top"|Na zdjęciu pokazane są prążki interferencyjne uzyskane na ekranie za siatką dyfrakcyjną oświetloną światłem lampy sodowej. Lampa taka emituje żółte światło monochromatyczne o długości fali 589,3 nm. Widzimy najmocniejszy prążek rzędu zerowego, obserwowany pod kątem <math>\theta=0^\circ\ </math>,, trochę słabsze prążki rzędu pierwszego i najsłabsze prążki rzędu drugiego. | ||
|} | |} | ||
| Linia 287: | Linia 287: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="450px" valign="top"|[[Grafika:PF_M16_Slajd25.png]] | |width="450px" valign="top"|[[Grafika:PF_M16_Slajd25.png]] | ||
|valign="top"|Jeśli oświetlimy siatkę światłem, które jest mieszaniną fal o różnych długościach, to zgodnie ze wzorem <math> | |valign="top"|Jeśli oświetlimy siatkę światłem, które jest mieszaniną fal o różnych długościach, to zgodnie ze wzorem <math>sin\theta=n\frac{\lambda}{d}</math> , otrzymamy wzmocnienia dla różnych długości fal pod różnymi kątami. Światło zostanie rozdzielone według długości fal – otrzymamy widmo światła. Na zdjęciu widzimy widmo światła lampy neonowej Prążek rzędu zerowego jest jeden, bo dla każdej barwy pojawia się pod kątem <math>\theta=0^\circ\ </math>,. Widzimy mieszaninę barw, którą odbieramy jako barwę różową. Natomiast prążków rzędu pierwszego jest tyle, ile poszczególnych barw składowych. Światło o najmniejszej długości fali, fioletowe, ma maksimum pod najmniejszym kątem <math>\theta\ </math>,. | ||
|} | |} | ||
| Linia 295: | Linia 295: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="450px" valign="top"|[[Grafika:PF_M16_Slajd26.png]] | |width="450px" valign="top"|[[Grafika:PF_M16_Slajd26.png]] | ||
|valign="top"|Zastanówmy się, jak duża musi być różnica długości fal, aby można było rozdzielić je za pomocą siatki dyfrakcyjnej. Gdyby źródło emitowało dwie fale takie, że różnica ich długości byłaby równa <math>\Delta \lambda=\lambda' -\lambda</math> , to możemy je rozróżnić, jeśli maksimum dla jednej fali przypada na pierwsze minimum drugiej. Położenie n-tego maksimum i pierwszego przy nim minimum dla fali o długości <math>\lambda\ | |valign="top"|Zastanówmy się, jak duża musi być różnica długości fal, aby można było rozdzielić je za pomocą siatki dyfrakcyjnej. Gdyby źródło emitowało dwie fale takie, że różnica ich długości byłaby równa <math>\Delta \lambda=\lambda' -\lambda</math> , to możemy je rozróżnić, jeśli maksimum dla jednej fali przypada na pierwsze minimum drugiej. Położenie n-tego maksimum i pierwszego przy nim minimum dla fali o długości <math>\lambda\ </math>, określają zależności: | ||
: <math> | : <math>sin\theta_n=n\frac{\lambda}{d}</math> , <math>sin{\theta_n}^{min}=n\frac{\lambda}{d}+\frac{\lambda}{Nd}</math> | ||
Maksimum drugiej fali o długości <math>\lambda'\ | Maksimum drugiej fali o długości <math>\lambda'\ </math>, musi być nie bliżej niż pierwsze minimum pierwszej fali, czyli musi być spełniony warunek: | ||
: <math> | : <math>n\frac{\lambda'}{d}=n\frac{\lambda}{d}+\frac{\lambda}{Nd}</math> , czyli <math>n(\lambda'-\lambda)=\frac{\lambda}{N}</math> | ||
Wielkość <math>R=\frac{\lambda}{\Delta \lambda}</math> nazywamy zdolnością rozdzielczą siatki dyfrakcyjnej. Widzimy, że: | Wielkość <math>R=\frac{\lambda}{\Delta \lambda}</math> nazywamy zdolnością rozdzielczą siatki dyfrakcyjnej. Widzimy, że: | ||
: <math> | : <math>R=\frac{\lambda}{\Delta \lambda}=nN</math> | ||
Wniosek stąd, że dla uzyskania dużej zdolności rozdzielczej należy stosować siatki o wielkiej liczbie szczelin i analizować widma wysokiego rzędu. | Wniosek stąd, że dla uzyskania dużej zdolności rozdzielczej należy stosować siatki o wielkiej liczbie szczelin i analizować widma wysokiego rzędu. | ||
| Linia 319: | Linia 319: | ||
Efekty dyfrakcyjne możemy obserwować nie tylko dla światła widzialnego i dla fal przechodzących przez szczeliny. Ważną i wartościową z punktu widzenia badania struktur krystalicznych jest dyfrakcja odbiciowa wiązek promieni Roentgena na kryształach. Zjawisko dyfrakcji zachodzi na zbudowanej z atomów sieci krystalicznej i polega na nałożeniu się fal odbitych od płaszczyzn utworzonych przez atomy. Kryształ stanowi rodzaj trójwymiarowej siatki dyfrakcyjnej dla promieniowania o długościach fal porównywalnych z odległościami międzyatomowymi w krysztale. | Efekty dyfrakcyjne możemy obserwować nie tylko dla światła widzialnego i dla fal przechodzących przez szczeliny. Ważną i wartościową z punktu widzenia badania struktur krystalicznych jest dyfrakcja odbiciowa wiązek promieni Roentgena na kryształach. Zjawisko dyfrakcji zachodzi na zbudowanej z atomów sieci krystalicznej i polega na nałożeniu się fal odbitych od płaszczyzn utworzonych przez atomy. Kryształ stanowi rodzaj trójwymiarowej siatki dyfrakcyjnej dla promieniowania o długościach fal porównywalnych z odległościami międzyatomowymi w krysztale. | ||
Przykład struktury sieci, przedstawiony w dwóch wymiarach, pokazuje rysunek. Kolorem czerwonym zaznaczone są węzły sieci, na których zachodzi zjawisko dyfrakcji. Odległość pomiędzy płaszczyznami poziomymi wynosi <math>d\ | Przykład struktury sieci, przedstawiony w dwóch wymiarach, pokazuje rysunek. Kolorem czerwonym zaznaczone są węzły sieci, na których zachodzi zjawisko dyfrakcji. Odległość pomiędzy płaszczyznami poziomymi wynosi <math>d\ </math>,. Kąt między płaszczyzną kryształu a promieniami padającymi równy jest <math>\theta\ </math>,. Padające na kolejne płaszczyzny fale płaskie ulegają odbiciu i jeśli różnica dróg optycznych fal odbitych od poszczególnych warstw równa jest całkowitej wielokrotności długości fali padającej, to wypadkowa fala odbita ma maksymalną amplitudę. Warunek powstawania maksimów dyfrakcyjnych zwany jest prawem Bragga i wynika bezpośrednio z zależności geometrycznych widocznych na rysunku. Aby po odbiciu uformowane zostało czoło zgodnych w fazie fal musi być spełniony warunek <math>2d sin\theta=n\lambda</math> , gdzie <math>n=1, 2, 3,...\ </math>, | ||
Prawo Bragga znajduje zastosowanie do badania struktury sieci krystalicznej, na przykład określania odległości międzypłaszczyznowych. Z drugiej strony, umożliwia także analizę składu widmowego promieniowania Roentgena, stanowiąc element metod spektroskopii rentgenowskiej. Stosując kryształy o znanych parametrach sieci krystalicznej, można określić długość padającej fali, stosując promieniowanie o znanej długości można określić odległości pomiędzy płaszczyznami struktury krystalicznej. Z kolei, jeśli na określony kryształ rzucimy wiązkę promieniowania o różnych długościach fali (niemonochromatycznego), to w wyniku odbicia braggowskiego możemy otrzymać promieniowanie monochromatyczne o długościach fali spełniających prawo Bragga. | Prawo Bragga znajduje zastosowanie do badania struktury sieci krystalicznej, na przykład określania odległości międzypłaszczyznowych. Z drugiej strony, umożliwia także analizę składu widmowego promieniowania Roentgena, stanowiąc element metod spektroskopii rentgenowskiej. Stosując kryształy o znanych parametrach sieci krystalicznej, można określić długość padającej fali, stosując promieniowanie o znanej długości można określić odległości pomiędzy płaszczyznami struktury krystalicznej. Z kolei, jeśli na określony kryształ rzucimy wiązkę promieniowania o różnych długościach fali (niemonochromatycznego), to w wyniku odbicia braggowskiego możemy otrzymać promieniowanie monochromatyczne o długościach fali spełniających prawo Bragga. | ||
| Linia 341: | Linia 341: | ||
Kiedy stoimy przy drodze i mija nas samochód, zauważamy, że wysokość dźwięku silnika nagle zmniejsza się - dźwięk staje się "niższy", kiedy samochód zaczyna się od nas oddalać. Zjawisko to, zwane efektem Dopplera, obserwowane jest nie tylko dla fali dźwiękowej, ale także dla fal elektromagnetycznych. Najpierw omówimy mechanizm tego zjawiska na przykładzie podłużnej fali dźwiękowej. | Kiedy stoimy przy drodze i mija nas samochód, zauważamy, że wysokość dźwięku silnika nagle zmniejsza się - dźwięk staje się "niższy", kiedy samochód zaczyna się od nas oddalać. Zjawisko to, zwane efektem Dopplera, obserwowane jest nie tylko dla fali dźwiękowej, ale także dla fal elektromagnetycznych. Najpierw omówimy mechanizm tego zjawiska na przykładzie podłużnej fali dźwiękowej. | ||
Kiedy fala dźwiękowa o długości <math>\lambda\ | Kiedy fala dźwiękowa o długości <math>\lambda\ </math>, rozchodzi się z prędkością <math>v\ </math>,, a my nie poruszamy się względem źródła, to w czasie <math>t\ </math>, dociera do nas <math>n=vt/{\lambda}</math> pełnych długości fal. Odpowiada to częstotliwości dźwięku <math>\nu=v/{\lambda}=n/t</math>. Kiedy zbliżamy się do źródła dźwięku z prędkością <math>v_0\ </math>,, to dodatkowo dociera do nas jeszcze <math>n_0=v_0t/{\lambda}</math> długości fal. Odpowiada to częstotliwości: | ||
: <math> | : <math>\nu'=\frac{(n+n_0)}{t}=\frac{\frac{vt}{\lambda}+\frac{v_0 t}{\lambda}}{t}=\frac{v+v_0}{\lambda}</math> | ||
|} | |} | ||
| Linia 353: | Linia 353: | ||
|valign="top"|Ponieważ <math>\lambda=v/{\nu}</math> otrzymujemy: | |valign="top"|Ponieważ <math>\lambda=v/{\nu}</math> otrzymujemy: | ||
: <math> | : <math>\nu'=\frac{\nu}{v}(v+v_0)=\nu\left(1+\frac{v_0}{v} \right)</math> | ||
a więc częstotliwość dźwięku odbierana przez obserwatora zbliżającego się do nieruchomego źródła, <math>\nu'\ | a więc częstotliwość dźwięku odbierana przez obserwatora zbliżającego się do nieruchomego źródła, <math>\nu'\ </math>,, jest większa od częstotliwości wysyłanej przez źródło, <math>\nu\ </math>,. Odbierany dźwięk jest wyższy. | ||
Kiedy oddalamy się od nieruchomego źródła dźwięku to zmniejsza się liczba fal docierających do nas w danym czasie i ton słyszanego dźwięku jest niższy. Rozumując jak wyżej, mamy bowiem: | Kiedy oddalamy się od nieruchomego źródła dźwięku to zmniejsza się liczba fal docierających do nas w danym czasie i ton słyszanego dźwięku jest niższy. Rozumując jak wyżej, mamy bowiem: | ||
: <math> | : <math>\nu'=\nu \left(1-\frac{v_0}{v} \right)</math> | ||
a więc częstotliwość dźwięku odbieranego jest mniejsza od częstotliwości dźwięku wysyłanego. | a więc częstotliwość dźwięku odbieranego jest mniejsza od częstotliwości dźwięku wysyłanego. | ||
| Linia 369: | Linia 369: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="450px" valign="top"|[[Grafika:PF_M16_Slajd31.png]] | |width="450px" valign="top"|[[Grafika:PF_M16_Slajd31.png]] | ||
|valign="top"|Kiedy my się nie poruszamy, ale porusza się w naszym kierunku źródło dźwięku (na przykład zbliżający się samochód), to obrazowo możemy powiedzieć, że źródło (samochód) stara się dogonić uciekającą falę. W czasie jednego okresu fala przesunie się o odcinek <math>vT=\lambda</math> , ale źródło przesunie się o odcinek <math>s_z=v_z T</math> , gdzie <math>v_z\ | |valign="top"|Kiedy my się nie poruszamy, ale porusza się w naszym kierunku źródło dźwięku (na przykład zbliżający się samochód), to obrazowo możemy powiedzieć, że źródło (samochód) stara się dogonić uciekającą falę. W czasie jednego okresu fala przesunie się o odcinek <math>vT=\lambda</math> , ale źródło przesunie się o odcinek <math>s_z=v_z T</math> , gdzie <math>v_z\ </math>, jest prędkością źródła. Długość fali będzie więc zmniejszona o odcinek jaki przebywa źródło w czasie jednego okresu: | ||
: <math>\lambda'=\lambda-s_z=(v-v_z)T=\frac{v-v_z}{\nu}</math> | : <math>\lambda'=\lambda-s_z=(v-v_z)T=\frac{v-v_z}{\nu}</math> | ||
| Linia 375: | Linia 375: | ||
Mniejsza długość fali odpowiada większej częstotliwości dźwięku. Częstotliwość docierającej do nas fali dźwiękowej będzie więc: | Mniejsza długość fali odpowiada większej częstotliwości dźwięku. Częstotliwość docierającej do nas fali dźwiękowej będzie więc: | ||
: <math> | : <math>\nu'=\frac{v}{\lambda'}=\frac{v\nu}{v-v_z}=\nu\frac{v}{v-v_z}</math> | ||
czyli <math>\nu'>\nu</math> , co oznacza, że dźwięk odbierany jest wyższy niż wysyłany. | czyli <math>\nu'>\nu</math> , co oznacza, że dźwięk odbierany jest wyższy niż wysyłany. | ||
| Linia 386: | Linia 386: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="450px" valign="top"|[[Grafika:PF_M16_Slajd32.png]] | |width="450px" valign="top"|[[Grafika:PF_M16_Slajd32.png]] | ||
|valign="top"|Kiedy źródło dźwięku się oddala, to ton dźwięku staje się niższy. W czasie jednego okresu źródło oddala się od nas o odcinek równy <math>s_z\ | |valign="top"|Kiedy źródło dźwięku się oddala, to ton dźwięku staje się niższy. W czasie jednego okresu źródło oddala się od nas o odcinek równy <math>s_z\ </math>, i o tyle powiększona jest długość fali. Rozumując analogicznie jak w przypadku zbliżania się źródła dźwięku otrzymujemy wyrażenie na częstotliwość fali docierającej do nas od oddalającego się źródła: | ||
: <math> | : <math>\nu'=\nu\frac{v}{v+v_z}</math> , | ||
czyli <math>\nu'<\nu</math>. | czyli <math>\nu'<\nu</math>. | ||
| Linia 394: | Linia 394: | ||
Obydwa przypadki, ruchu źródła i ruchu obserwatora, można ująć w postaci jednego wzoru: | Obydwa przypadki, ruchu źródła i ruchu obserwatora, można ująć w postaci jednego wzoru: | ||
: <math> | : <math>\nu'=\nu\frac{v\pm v_0}{v\mp v_z}</math> , | ||
gdzie górne znaki odpowiadają zbliżaniu, a dolne oddalaniu się obiektów. | gdzie górne znaki odpowiadają zbliżaniu, a dolne oddalaniu się obiektów. | ||
| Linia 404: | Linia 404: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="450px" valign="top"|[[Grafika:PF_M16_Slajd33.png]] | |width="450px" valign="top"|[[Grafika:PF_M16_Slajd33.png]] | ||
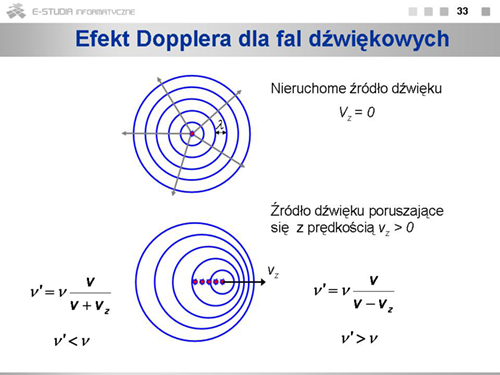
|valign="top"|Ilustracja pokazuje mechanizm zmiany długości fali dźwiękowej, gdy źródło porusza się. Na górnym rysunku źródło jest nieruchome i powierzchnie falowe wyemitowane w równych odstępach czasu <math>T\ | |valign="top"|Ilustracja pokazuje mechanizm zmiany długości fali dźwiękowej, gdy źródło porusza się. Na górnym rysunku źródło jest nieruchome i powierzchnie falowe wyemitowane w równych odstępach czasu <math>T\ </math>, we wszystkich kierunkach odległe są o <math>\lambda\ </math>,. Na dolnym rysunku źródło porusza się w prawo i kolejne powierzchnie falowe wyemitowane są w punktach przesuniętych o <math>s_z=v_z T</math> , co daje efekt zmniejszenia długości fali z prawej strony i zwiększenia z lewej. | ||
|} | |} | ||
| Linia 412: | Linia 412: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="450px" valign="top"|[[Grafika:PF_M16_Slajd34.png]] | |width="450px" valign="top"|[[Grafika:PF_M16_Slajd34.png]] | ||
|valign="top"|Dopplerowska zmiana częstotliwości dla fal dźwiękowych zależna jest od prędkości ruchu źródła i obserwatora względem ośrodka, w którym rozchodzą się fale dźwiękowe. Efekt Dopplera występuje również dla fal elektromagnetycznych. Ale naszego rozumowania dla fal dźwiękowych nie możemy powtórzyć dla fal elektromagnetycznych, bo nie istnieje żaden ośrodek, który byłby nośnikiem fal elektromagnetycznych. Fala elektromagnetyczna rozchodzi się w próżni, a jej prędkość jest w każdym układzie taka sama i wynosi <math>c\ | |valign="top"|Dopplerowska zmiana częstotliwości dla fal dźwiękowych zależna jest od prędkości ruchu źródła i obserwatora względem ośrodka, w którym rozchodzą się fale dźwiękowe. Efekt Dopplera występuje również dla fal elektromagnetycznych. Ale naszego rozumowania dla fal dźwiękowych nie możemy powtórzyć dla fal elektromagnetycznych, bo nie istnieje żaden ośrodek, który byłby nośnikiem fal elektromagnetycznych. Fala elektromagnetyczna rozchodzi się w próżni, a jej prędkość jest w każdym układzie taka sama i wynosi <math>c\ </math>,. | ||
Prędkości źródła i obserwatora względem ośrodka musimy zastąpić prędkością względną tych dwóch układów. Załóżmy, że fala o częstotliwości <math>\nu\ | Prędkości źródła i obserwatora względem ośrodka musimy zastąpić prędkością względną tych dwóch układów. Załóżmy, że fala o częstotliwości <math>\nu\ </math>, emitowana jest w układzie <math>U\ </math>,. Jaka częstotliwość <math>\nu'\ </math>, będzie obserwowana w układzie <math>U'\ </math>, poruszającym się względem <math>U\ </math>, z prędkością względną <math>v_{wzgl}\ </math>, ? Aby rozwiązać ten problem, należy zastosować transformację Lorentza, czyli wyrazić współrzędne w układzie <math>U'\ </math>,: <math>x'\ </math>, i <math>t'\ </math>, przez współrzędne w układzie <math>U\ </math>,: <math>x\ </math>, i <math>t\ </math>,. Pominiemy szczegółowe rachunki i podamy od razu wynik końcowy. | ||
: <math> | : <math>\nu'=\nu\sqrt{\frac{1\mp\frac{v_{wzgl}}{c}}{1\pm\frac{v_{wzgl}}{c}}}</math> | ||
gdzie górne znaki odpowiadają oddalaniu się obserwatora i źródła (dając <math>\nu'<\nu</math>), a dolne - zbliżaniu (dając <math>\nu'>\nu</math>). | gdzie górne znaki odpowiadają oddalaniu się obserwatora i źródła (dając <math>\nu'<\nu</math>), a dolne - zbliżaniu (dając <math>\nu'>\nu</math>). | ||
| Linia 430: | Linia 430: | ||
= Podsumowanie = | = Podsumowanie = | ||
Zjawiska związane z nakładaniem się fal noszą nazwę interferencji fal. Jeśli fala przechodzi przez dwie szczeliny, to na ekranie za przesłoną powstają jasne i ciemne prążki. Warunek na powstanie jasnego prążka, czyli na wzmocnienie, to: <math>d sin\theta=n\lambda</math> , gdzie <math>d\ | Zjawiska związane z nakładaniem się fal noszą nazwę interferencji fal. Jeśli fala przechodzi przez dwie szczeliny, to na ekranie za przesłoną powstają jasne i ciemne prążki. Warunek na powstanie jasnego prążka, czyli na wzmocnienie, to: <math>d sin\theta=n\lambda</math> , gdzie <math>d\ </math>, jest odległością między szczelinami, <math>\lambda\ </math>, - długością fali, <math>\theta\ </math>, - kątem obserwacji, a <math>n=1, 2, 3,...\ </math>, nazywamy rzędem widma. Ogólnie, dwie nakładające się fale wzmacniają się, jeśli różnica ich faz wynosi zero, natomiast całkowicie wygaszają się, gdy różnica faz równa jest <math>\pi\ </math>,. | ||
Kiedy światło przechodzi przez otwór obserwujemy dyfrakcję, czyli ugięcie światła. W tym przypadku również powstają za otworem jasne i ciemne prążki. Całkowite wygaszenie, czyli ciemne prążki, obserwujemy pod kątem <math>\theta\ | Kiedy światło przechodzi przez otwór obserwujemy dyfrakcję, czyli ugięcie światła. W tym przypadku również powstają za otworem jasne i ciemne prążki. Całkowite wygaszenie, czyli ciemne prążki, obserwujemy pod kątem <math>\theta\ </math>, danym wzorem: <math>h sin\theta=n\lambda</math> , gdzie <math>h\ </math>, jest szerokością szczeliny. Intensywność prążków dyfrakcyjnych zależna jest od stosunku szerokości szczeliny do długości fali i wyraża się wzorem: <math>I_{\theta}=I_0 \left(\frac{sin\alpha}{\alpha} \right)^2</math> , gdzie <math>\alpha=\frac{\pi}{\lambda}h sin\theta</math> | ||
W układzie dwóch szczelin występuje superpozycja obu efektów: dyfrakcji i interferencji. Obserwuje się szereg maksimów interferencyjnych, których intensywność określona jest przez efekty dyfrakcyjne. Intensywność prążków opisuje wzór: <math> | W układzie dwóch szczelin występuje superpozycja obu efektów: dyfrakcji i interferencji. Obserwuje się szereg maksimów interferencyjnych, których intensywność określona jest przez efekty dyfrakcyjne. Intensywność prążków opisuje wzór: <math>I_{\theta_{id}}=I_m (cos\alpha_i)^2\cdot \left(\frac{sin\alpha_d}{\alpha_d} \right)^2</math> , gdzie <math>\alpha_i= \frac{\pi d}{\lambda} sin\theta</math> a <math>\alpha_d= \frac{\pi h}{\lambda} sin\theta</math> .Czynnik <math>(cos\alpha_i)^2\ </math>, jest związany z efektami interferencyjnymi, a czynnik <math>\left(\frac{sin\alpha_d}{\alpha_d} \right)^2</math> z efektami dyfrakcyjnymi. | ||
Siatka dyfrakcyjna to układ wielu szczelin. Światło przechodząc przez siatkę tworzy wąskie prążki interferencyjne, których położenie określone jest wzorem <math>sin\theta=n\frac{\lambda}{d}</math> .Zdolność rozdzielczą siatki definiujemy <math> | Siatka dyfrakcyjna to układ wielu szczelin. Światło przechodząc przez siatkę tworzy wąskie prążki interferencyjne, których położenie określone jest wzorem <math>sin\theta=n\frac{\lambda}{d}</math> .Zdolność rozdzielczą siatki definiujemy <math>R=\frac{\lambda}{\Delta \lambda}</math> , gdzie <math>\lambda\ </math>, to długość fali, a <math>\Delta \lambda=\lambda'-\lambda</math> jest najmniejszą różnicą długości fal, które można rozdzielić za pomocą siatki. Zdolność rozdzielcza jest tym większa, im większą liczbę szczelin zawiera siatka i im dalsze rzędy widma analizujemy. | ||
'''Prawo Bragga określa warunek powstawania maksimów dyfrakcyjnych promieniowania rentgenowskiego odbitego od płaszczyzny kryształu: <math>2d sin\theta=n\lambda</math> , gdzie <math>d\ | '''Prawo Bragga określa warunek powstawania maksimów dyfrakcyjnych promieniowania rentgenowskiego odbitego od płaszczyzny kryształu: <math>2d sin\theta=n\lambda</math> , gdzie <math>d\ </math>, jest odległością między płaszczyznami sieci krystalicznej, <math>\theta\ </math>, - kąt między kierunkiem promieniowania a płaszczyzną kryształu, <math>\lambda\ </math>, - długością fali, a <math>n=1, 2, 3,...\ </math>,''' Prawo Bragga znajduje zastosowanie do badania struktury sieci krystalicznej. | ||
Efekt Dopplera polega na zależności częstości fali od prędkości źródła fali i prędkości obserwatora. Dla fali dźwiękowej zależność ta jest następująca: | Efekt Dopplera polega na zależności częstości fali od prędkości źródła fali i prędkości obserwatora. Dla fali dźwiękowej zależność ta jest następująca: | ||
: <math> | : <math>\nu'=\nu\frac{v\pm v_0}{v\mp v_z}</math> , | ||
gdzie <math>v_0\ | gdzie <math>v_0\ </math>, to prędkość obserwatora, <math>v_z\ </math>, – prędkość źródła fali, <math>v\ </math>, - prędkość rozchodzenia się fali w ośrodku, <math>\nu\ </math>, - częstość emitowana, <math>\nu'\ </math>, – częstość obserwowana. Górne znaki odpowiadają zbliżaniu, a dolne oddalaniu się obiektów. | ||
Dla fal elektromagnetycznych efekt Dopplera opisuje wzór: | Dla fal elektromagnetycznych efekt Dopplera opisuje wzór: | ||
: <math> | : <math>\nu'=\nu\sqrt{\frac{1\mp\frac{v_{wzgl}}{c}}{1\pm\frac{v_{wzgl}}{c}}}</math> | ||
gdzie <math>v_{wzgl}\ | gdzie <math>v_{wzgl}\ </math>, jest prędkością względną obserwatora i źródła światła. Górne znaki odpowiadają oddalaniu się obserwatora i źródła (dając <math>\nu'<\nu</math>), a dolne - zbliżaniu (dając <math>\nu'>\nu</math>). | ||
<hr width="100%"> | <hr width="100%"> | ||
| Linia 465: | Linia 465: | ||
Warunek na wzmocnienie: <math>m\lambda=d sin\alpha_m</math> (*) | Warunek na wzmocnienie: <math>m\lambda=d sin\alpha_m</math> (*) | ||
gdzie: <math>d\ | gdzie: <math>d\ </math>, - stała siatki, <math>l\ </math>, - długość fali, <math>a_m\ </math>, - kąt ugięcia, a <math>m=1, 2, 3...\ </math>, jest rzędem widma, które można obserwować na ekranie w postaci jasnych prążków rozłożonych symetrycznie względem prążka zerowego (m = 0). | ||
W naszym zadaniu stałą siatki obliczymy z warunku (*). Ponieważ <math> | W naszym zadaniu stałą siatki obliczymy z warunku (*). Ponieważ <math>d=\frac{m\lambda}{sin\alpha_m}</math> , to dla m = 2, <math>d=\frac{2\cdot 589,6nm}{sin28^\circ 9'}</math> , więc stała siatki <math>d=2500 nm\ </math>,. | ||
Z warunku (*) sinusy kątów ugięcia są <math>sin\alpha_m=\frac{m\lambda}{d}</math> , a dla prążków pierwszego rzędu (m = 1) | Z warunku (*) sinusy kątów ugięcia są <math>sin\alpha_m=\frac{m\lambda}{d}</math> , a dla prążków pierwszego rzędu (m = 1) | ||
<math> | <math>\alpha_1=arc sin\frac{\lambda}{d}=13^\circ 38'</math> . | ||
</div></div> | </div></div> | ||
| Linia 489: | Linia 489: | ||
Jeżeli źródło fali i obserwator, zbliżają się do siebie w ośrodku przenoszącym falę, to obserwator słyszy dźwięk o częstotliwości: | Jeżeli źródło fali i obserwator, zbliżają się do siebie w ośrodku przenoszącym falę, to obserwator słyszy dźwięk o częstotliwości: | ||
: <math> | : <math>\nu'=\nu \left(\frac{v+v_0}{v-v_z} \right)</math> | ||
gdzie: <math>\nu\ | gdzie: <math>\nu\ </math>, - częstotliwość fali emitowanej przez źródło, <math>v\ </math>, - prędkość rozchodzenia się fali w ośrodku, <math>v_0\ </math>, - prędkość obserwatora, <math>v_z\ </math>, - prędkość źródła. | ||
Jeżeli źródło fali i obserwator, oddalają się od siebie w ośrodku przenoszącym falę, to obserwator odbiera dźwięk o częstotliwości: | Jeżeli źródło fali i obserwator, oddalają się od siebie w ośrodku przenoszącym falę, to obserwator odbiera dźwięk o częstotliwości: | ||
: <math> | : <math>\nu'=\nu \left(\frac{v-v_0}{v+v_z} \right)</math> | ||
Do obliczenia częstotliwości fali słyszanej przez maszynistę drugiego pociągu podstawiamy do podanych wzorów dane liczbowe: <math>\nu=500Hz</math> , <math>v=340 m/s</math> , <math>v_0=54 km/godz = 15 m/s</math> , <math>v_z=72 km/godz = 20 m/s</math> . | Do obliczenia częstotliwości fali słyszanej przez maszynistę drugiego pociągu podstawiamy do podanych wzorów dane liczbowe: <math>\nu=500Hz</math> , <math>v=340 m/s</math> , <math>v_0=54 km/godz = 15 m/s</math> , <math>v_z=72 km/godz = 20 m/s</math> . | ||
| Linia 517: | Linia 517: | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | ||
Dodatkowa szerokość pasma związana z dyfrakcją wynosi: <math>y_d=\theta_{min}D</math> . <math>\theta_{min}\ | Dodatkowa szerokość pasma związana z dyfrakcją wynosi: <math>y_d=\theta_{min}D</math> . <math>\theta_{min}\ </math>, to kąt pod jakim obserwujemy pierwsze minimum, które wyznacza szerokość głównego maksimum. | ||
Korzystamy z warunku na pierwsze minimum: <math> | Korzystamy z warunku na pierwsze minimum: <math>sin\theta_{min}=\frac{\lambda}{h}</math> . Ponieważ dla małych kątów <math>sin\alpha \approx \alpha</math> możemy zapisać: <math>y_d=\theta_{min}D=\left(\frac{\lambda}{h} \right)D</math>. Całkowita szerokość jest równa: <math>y=h+\frac{\lambda D}{h}</math>. | ||
Szukamy minimum funkcji y(h): | Szukamy minimum funkcji y(h): | ||
<math>\frac{dy}{dh}=0</math> , stąd <math> | <math>\frac{dy}{dh}=0</math> , stąd <math>\left(1-\frac{\lambda D}{h^2} \right)=0</math> . Szerokość pasma jest najmniejsza przy szerokości szczeliny: <math>h=\sqrt{\lambda D}</math> . | ||
</div></div> | </div></div> | ||
| Linia 531: | Linia 531: | ||
''' Zadanie 4''' | ''' Zadanie 4''' | ||
Światło lampy neonowej przepuszczono przez siatkę dyfrakcyjną i uzyskano na ekranie prążki dyfrakcyjne. Obliczyć długości fal linii widmowych barwy: fioletowej, niebieskiej, zielonej i czerwonej, jeśli odpowiednie prążki pierwszego rzędu obserwuje się pod kątami: <math>5^\circ 7'\ | Światło lampy neonowej przepuszczono przez siatkę dyfrakcyjną i uzyskano na ekranie prążki dyfrakcyjne. Obliczyć długości fal linii widmowych barwy: fioletowej, niebieskiej, zielonej i czerwonej, jeśli odpowiednie prążki pierwszego rzędu obserwuje się pod kątami: <math>5^\circ 7'\ </math>,, <math>5^\circ 46'\ </math>, , <math>6^\circ 12'\ </math>, , <math>7^\circ 21'\ </math>, , a stała siatki dyfrakcyjnej d = 5000 nm. | ||
| Linia 544: | Linia 544: | ||
''' Zadanie 5''' | ''' Zadanie 5''' | ||
W roku 2002 odkryto za pomocą teleskopu SUBARU galaktykę, której światło wykazuje przesunięcie ku czerwieni z = 6,54. Przesunięcie ku czerwieni zdefiniowane jest jako <math> | W roku 2002 odkryto za pomocą teleskopu SUBARU galaktykę, której światło wykazuje przesunięcie ku czerwieni z = 6,54. Przesunięcie ku czerwieni zdefiniowane jest jako <math>z=\frac{\lambda_{obs}-\lambda_{em}}{\lambda_{em}}</math> , gdzie <math>\lambda_{em}\ </math>, jest długością fali wyemitowaną z galaktyki, a <math>\lambda_{obs}\ </math>, jest długością fali zaobserwowaną na Ziemi. Obliczyć, z jaką prędkością galaktyka oddala się od Ziemi. | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | ||
Zastosujmy wzór na częstotliwość obserwowaną: <math> | Zastosujmy wzór na częstotliwość obserwowaną: <math>\nu_{ob}=\nu_{em}\sqrt{\frac{1-\frac{v}{c}}{ 1+\frac{v}{c}}}</math> , gdzie <math>v\ </math>, jest prędkością oddalania się galaktyki. Ponieważ <math>\nu=\frac{c}{\lambda}</math> , możemy zapisać: <math>\frac{\lambda_{em}}{\lambda_{ob}}=\sqrt{\frac{1-\beta}{1+\beta}}</math> . Przez <math>\beta\ </math>, oznaczyliśmy stosunek prędkości galaktyki do prędkości światła. Korzystając z definicji przesunięcia ku czerwieni, mamy: <math>z=\frac{\lambda_{obs}}{\lambda_{em}}-1</math> , czyli <math>\frac{\lambda_{em}}{\lambda_{ob}}=\frac{1}{1+z}=0,1325</math> . Podstawiając tę wartość do powyższego wzoru, otrzymujemy: <math>0,1325^2=\frac{1-\beta}{1+\beta}</math> , skąd obliczamy: <math>\beta= 0,965</math>. | ||
Odp. Galaktyka oddala się od Ziemi z prędkością bardzo bliską prędkości światła, a mianowicie: <math>v = 0,965\cdot c</math>. Dodajmy, że taka prędkość ucieczki oznacza, że galaktyka odległa jest o 12,9 mld lat świetlnych i że powstała, gdy Wszechświat był bardzo młody – liczył sobie mniej niż <math>1\%\ | Odp. Galaktyka oddala się od Ziemi z prędkością bardzo bliską prędkości światła, a mianowicie: <math>v = 0,965\cdot c</math>. Dodajmy, że taka prędkość ucieczki oznacza, że galaktyka odległa jest o 12,9 mld lat świetlnych i że powstała, gdy Wszechświat był bardzo młody – liczył sobie mniej niż <math>1\%\ </math>, obecnego wieku. | ||
</div></div> | </div></div> | ||
Aktualna wersja na dzień 12:02, 5 wrz 2023
Wykład

|
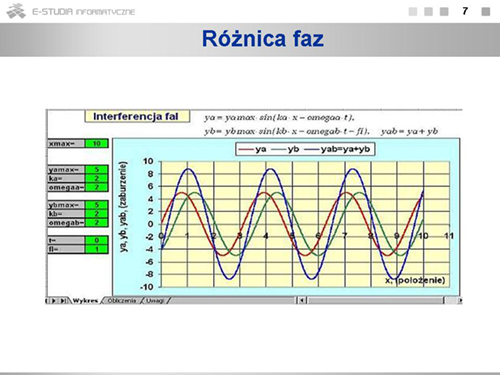
|
Ilustracja przedstawia złożenie dwóch fal różniących się fazą. Kiedy inne parametry fal (na przykład częstość, amplituda) będą się różnić, fala wypadkowa nie musi być falą sinusoidalną. |
Podsumowanie
Zjawiska związane z nakładaniem się fal noszą nazwę interferencji fal. Jeśli fala przechodzi przez dwie szczeliny, to na ekranie za przesłoną powstają jasne i ciemne prążki. Warunek na powstanie jasnego prążka, czyli na wzmocnienie, to: , gdzie , jest odległością między szczelinami, , - długością fali, , - kątem obserwacji, a , nazywamy rzędem widma. Ogólnie, dwie nakładające się fale wzmacniają się, jeśli różnica ich faz wynosi zero, natomiast całkowicie wygaszają się, gdy różnica faz równa jest ,.
Kiedy światło przechodzi przez otwór obserwujemy dyfrakcję, czyli ugięcie światła. W tym przypadku również powstają za otworem jasne i ciemne prążki. Całkowite wygaszenie, czyli ciemne prążki, obserwujemy pod kątem , danym wzorem: , gdzie , jest szerokością szczeliny. Intensywność prążków dyfrakcyjnych zależna jest od stosunku szerokości szczeliny do długości fali i wyraża się wzorem: , gdzie
W układzie dwóch szczelin występuje superpozycja obu efektów: dyfrakcji i interferencji. Obserwuje się szereg maksimów interferencyjnych, których intensywność określona jest przez efekty dyfrakcyjne. Intensywność prążków opisuje wzór: , gdzie a .Czynnik , jest związany z efektami interferencyjnymi, a czynnik z efektami dyfrakcyjnymi.
Siatka dyfrakcyjna to układ wielu szczelin. Światło przechodząc przez siatkę tworzy wąskie prążki interferencyjne, których położenie określone jest wzorem .Zdolność rozdzielczą siatki definiujemy , gdzie , to długość fali, a jest najmniejszą różnicą długości fal, które można rozdzielić za pomocą siatki. Zdolność rozdzielcza jest tym większa, im większą liczbę szczelin zawiera siatka i im dalsze rzędy widma analizujemy.
Prawo Bragga określa warunek powstawania maksimów dyfrakcyjnych promieniowania rentgenowskiego odbitego od płaszczyzny kryształu: , gdzie , jest odległością między płaszczyznami sieci krystalicznej, , - kąt między kierunkiem promieniowania a płaszczyzną kryształu, , - długością fali, a , Prawo Bragga znajduje zastosowanie do badania struktury sieci krystalicznej.
Efekt Dopplera polega na zależności częstości fali od prędkości źródła fali i prędkości obserwatora. Dla fali dźwiękowej zależność ta jest następująca:
- ,
gdzie , to prędkość obserwatora, , – prędkość źródła fali, , - prędkość rozchodzenia się fali w ośrodku, , - częstość emitowana, , – częstość obserwowana. Górne znaki odpowiadają zbliżaniu, a dolne oddalaniu się obiektów.
Dla fal elektromagnetycznych efekt Dopplera opisuje wzór:
gdzie , jest prędkością względną obserwatora i źródła światła. Górne znaki odpowiadają oddalaniu się obserwatora i źródła (dając ), a dolne - zbliżaniu (dając ).
Materiały do ćwiczeń
Zadanie 1
Wiązka żółtego światła monochromatycznego o długości fali 589,3 nm pada prostopadle na siatkę dyfrakcyjną. Widmo dyfrakcyjne drugiego rzędu ( m = 2 ) obserwuje się pod kątem . Obliczyć stałą siatki dyfrakcyjnej oraz ocenić pod jakim kątem ugięcia obserwuje się prążki pierwszego rzędu ( m = 1 ).
Zadanie 2
Dwa pociągi poruszają się po torach równoległych. Pierwszy z prędkością 72 km/godz, a drugi z prędkością 54 km/godz. Gwizdek lokomotywy pierwszego pociągu wytwarza sygnał o częstotliwości 500 Hz. Jaką częstotliwość dźwięku słyszy maszynista drugiego pociągu, gdy pociągi:
- zbliżają się do siebie,
- oddalają się od siebie
Zadanie 3
Jeśli równoległa wiązka światła pada na szeroką szczelinę o szerokości h, na ekranie odległym o D pojawi się pasmo o szerokości y = h. Jeśli szczelinę stopniowo zmniejszamy, pasmo staje się coraz węższe, aż do momentu pojawienia się efektów dyfrakcyjnych. Wtedy pasmo znów się poszerza. Przy jakiej szerokości szczeliny otrzymamy najwęższe pasmo na ekranie?
Zadanie 4
Światło lampy neonowej przepuszczono przez siatkę dyfrakcyjną i uzyskano na ekranie prążki dyfrakcyjne. Obliczyć długości fal linii widmowych barwy: fioletowej, niebieskiej, zielonej i czerwonej, jeśli odpowiednie prążki pierwszego rzędu obserwuje się pod kątami: ,, , , , , , , a stała siatki dyfrakcyjnej d = 5000 nm.
Zadanie 5
W roku 2002 odkryto za pomocą teleskopu SUBARU galaktykę, której światło wykazuje przesunięcie ku czerwieni z = 6,54. Przesunięcie ku czerwieni zdefiniowane jest jako , gdzie , jest długością fali wyemitowaną z galaktyki, a , jest długością fali zaobserwowaną na Ziemi. Obliczyć, z jaką prędkością galaktyka oddala się od Ziemi.
Słowa kluczowe
- interferencja fal
- dyfrakcja
- siatka dyfrakcyjna
- prawo Bragga
- efekt Dopplera
Bibliografia
- J. Orear, Fizyka, WNT, Warszawa (1998);
- R. Resnick, D. Halliday, Fizyka 1, PWN, Warszawa (1994);
- I.W. Sawieliew, Wykłady z fizyki, PWN, Warszawa (1994).