PF Moduł 10: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
mNie podano opisu zmian |
m Zastępowanie tekstu – „,...,” na „,\ldots,” |
||
| (Nie pokazano 3 pośrednich wersji utworzonych przez tego samego użytkownika) | |||
| Linia 24: | Linia 24: | ||
To | To | ||
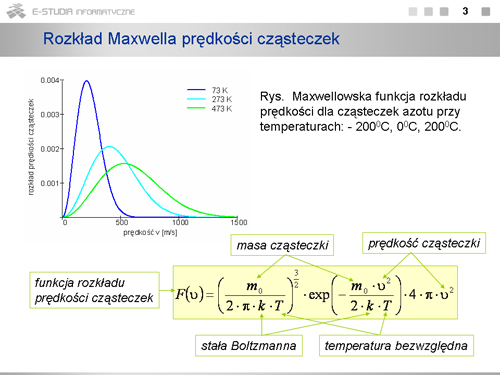
:Rozkład Maxwella opisuje prędkości cząsteczek gazu doskonałego będącego w stanie równowagi termodynamicznej, na który nie działają siły zewnętrzne. Pozwala obliczyć charakterystyczne wartości wielkości średnich: średnią prędkość kwadratową, średnią prędkość i prędkość najbardziej prawdopodobną oraz liczbę cząsteczek o prędkościach zawartych w przedziale wartości od <math>v\ | :Rozkład Maxwella opisuje prędkości cząsteczek gazu doskonałego będącego w stanie równowagi termodynamicznej, na który nie działają siły zewnętrzne. Pozwala obliczyć charakterystyczne wartości wielkości średnich: średnią prędkość kwadratową, średnią prędkość i prędkość najbardziej prawdopodobną oraz liczbę cząsteczek o prędkościach zawartych w przedziale wartości od <math>v\ </math>, do <math>v + dv\ </math>,. | ||
Jeżeli mamy <math>N\ | Jeżeli mamy <math>N\ </math>, cząsteczek, to liczba <math>dN_v\ </math>, cząsteczek o prędkościach w przedziale od <math>v\ </math>, do <math>v + dv\ </math>, będzie określona wzorem <math>dN_v=N\cdot F(v)\cdot dv</math> , gdzie <math>F(v)\ </math>, dane jest wzorem | ||
<math> | <math>F(v)=\left(\frac{m_0}{2\cdot \pi\cdot k\cdot T} \right)^{3/2}\cdot exp\left(-\frac{m_0\cdot v^2}{2\cdot k\cdot T} \right)\cdot 4\cdot \pi \cdot v^2</math> | ||
|} | |} | ||
| Linia 38: | Linia 38: | ||
|valign="top"|Wyprowadzenie wzoru można znaleźć w literaturze. | |valign="top"|Wyprowadzenie wzoru można znaleźć w literaturze. | ||
<math> | <math>F(v)=\left(\frac{m_0}{2\cdot \pi\cdot k\cdot T} \right)^{3/2}\cdot exp\left(-\frac{m_0\cdot v^2}{2\cdot k\cdot T} \right)\cdot 4\cdot \pi \cdot v^2</math> | ||
Co jest charakterystyczne w tym rozkładzie <math>F(v)\ | Co jest charakterystyczne w tym rozkładzie <math>F(v)\ </math>, ? Jest to konieczność wystąpienia maksimum ze względu na iloczyn rosnącej parabolicznie i malejącej wykładniczo zależności od <math>v\ </math>, . (Przeanalizuj dokładnie trzy człony wzoru na <math>F(v)\ </math>, . Pierwszy, to czynnik normalizacyjny zawierający wyłącznie wartości stałe, drugi - to człon wykładniczy, ale z ujemną wartością w wykładniku, czyli malejący ze wzrostem prędkości i równy jedynce dla <math>v=0</math>, , ostatni - rosnący paraboliczne ze wzrostem prędkości. Rezultat jest zobrazowany na wykresie maxwellowskiej funkcji rozkładu prędkości cząsteczek azotu przy temperaturach: <math>73 K\, (-200^\circ C)\ </math>, , <math>273 K\, (0^\circ C)\ </math>, , <math>473 K\, (200^\circ C)\ </math>,. Gdy temperatura rośnie maksimum krzywej rozkładu przesuwa się w stronę większych prędkości i krzywa ulega spłaszczeniu. Pole pod krzywą równe jest całkowitej liczbie cząsteczek w próbce i pozostaje stałe niezależnie od temperatury. | ||
Rozkład prędkości cząsteczek w danej temperaturze zależy od masy cząsteczek. Im mniejsza masa tym większa liczba cząsteczek o dużych prędkościach. | Rozkład prędkości cząsteczek w danej temperaturze zależy od masy cząsteczek. Im mniejsza masa tym większa liczba cząsteczek o dużych prędkościach. | ||
| Linia 50: | Linia 50: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="450px" valign="top"|[[Grafika:PF_M10_Slajd4.png]][[Grafika:PF_M10_Slajd5.png]] | |width="450px" valign="top"|[[Grafika:PF_M10_Slajd4.png]][[Grafika:PF_M10_Slajd5.png]] | ||
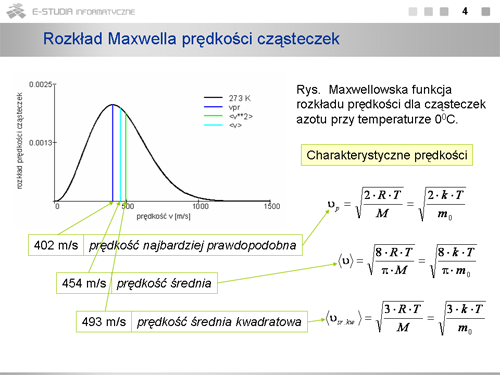
|valign="top"|Dla każdej temperatury można określić prędkość, która występuje najczęściej, czyli najwięcej cząsteczek ma prędkości bliskie tej wartości. Wartość ta odpowiada maksimum rozkładu Maxwella. Prędkość tę nazywamy prędkością najbardziej prawdopodobną, <math>v_p\ | |valign="top"|Dla każdej temperatury można określić prędkość, która występuje najczęściej, czyli najwięcej cząsteczek ma prędkości bliskie tej wartości. Wartość ta odpowiada maksimum rozkładu Maxwella. Prędkość tę nazywamy prędkością najbardziej prawdopodobną, <math>v_p\ </math>, . Można ją określić z matematycznego warunku na maksimum funkcji. | ||
:<math> | :<math>\frac{dF(v)}{dv}\Big|_{v=v_p}=0</math> | ||
Stąd otrzymuje się <math>v_p=\sqrt{2\cdot k\cdot T/m_0 }</math> , a więc <math>v_p<v_{sr. kw.}</math> jak to wynika z definicji średniej prędkości kwadratowej (teoria kinetyczna). | Stąd otrzymuje się <math>v_p=\sqrt{2\cdot k\cdot T/m_0 }</math> , a więc <math>v_p<v_{sr. kw.}</math> jak to wynika z definicji średniej prędkości kwadratowej (teoria kinetyczna). | ||
| Linia 65: | Linia 65: | ||
|width="450px" valign="top"|[[Grafika:PF_M10_Slajd6.png]]][[Grafika:PF_M10_Slajd7.png]] | |width="450px" valign="top"|[[Grafika:PF_M10_Slajd6.png]]][[Grafika:PF_M10_Slajd7.png]] | ||
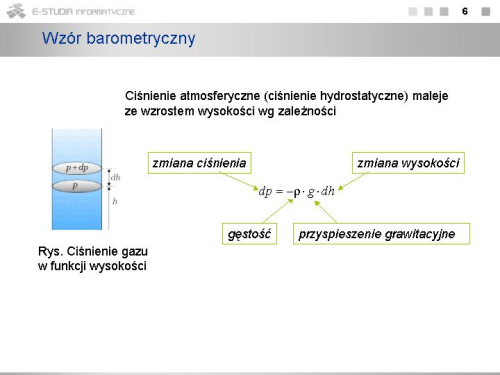
|valign="top"|Ciśnienie atmosferyczne w danym punkcie nad powierzchnią Ziemi określone jest przez ciężar warstwy powietrza leżącej powyżej tego punktu, powinno zależeć od wysokości. Im większa wysokość, tym mniejsza jest warstwa powietrza, więc i ciśnienie jest mniejsze. Różnica ciśnień <math>dp\ | |valign="top"|Ciśnienie atmosferyczne w danym punkcie nad powierzchnią Ziemi określone jest przez ciężar warstwy powietrza leżącej powyżej tego punktu, powinno zależeć od wysokości. Im większa wysokość, tym mniejsza jest warstwa powietrza, więc i ciśnienie jest mniejsze. Różnica ciśnień <math>dp\ </math>, związana ze wzrostem wysokości <math>dh\ </math>, ma znak ujemny i wynosi | ||
: <math>dp=-\rho \cdot g\cdot dh</math> | : <math>dp=-\rho \cdot g\cdot dh</math> | ||
gdzie <math>\rho\ | gdzie <math>\rho\ </math>, jest gęstością gazu na wysokości <math>h\ </math>, , a <math>g\ </math>, jest przyspieszeniem ziemskim na tej wysokości. | ||
Z dobrym przybliżeniem można potraktować powietrze jako gaz doskonały. Dzieląc obustronnie równanie stanu gazu doskonałego dla jednego mola <math>p\cdot V=R\cdot T</math> przez wartość średniej masy molowej powietrza, określonej z uwzględnieniem procentowej zawartości azotu, tlenu i pozostałych gazów w powietrzu, otrzymujemy | Z dobrym przybliżeniem można potraktować powietrze jako gaz doskonały. Dzieląc obustronnie równanie stanu gazu doskonałego dla jednego mola <math>p\cdot V=R\cdot T</math> przez wartość średniej masy molowej powietrza, określonej z uwzględnieniem procentowej zawartości azotu, tlenu i pozostałych gazów w powietrzu, otrzymujemy | ||
<math>p\cdot \begin{matrix} \underbrace{ (V/M) } \\ {1/{\rho}} \end{matrix}= | <math>p\cdot \begin{matrix} \underbrace{ (V/M) } \\ {1/{\rho}} \end{matrix}=\frac{R\cdot T}{M}</math> , czyli <math>\rho=\frac{M\cdot p}{R\cdot T}</math> | ||
Więc możemy napisać, że | Więc możemy napisać, że | ||
: <math> | : <math>dp=-\frac{M\cdot p\cdot g}{R\cdot T}\cdot dh</math> | ||
Otrzymujemy w ten sposób równanie różniczkowe o rozdzielonych zmiennych | Otrzymujemy w ten sposób równanie różniczkowe o rozdzielonych zmiennych | ||
: <math> | : <math>\frac{dp}{p}=-\frac{M \cdot g}{R\cdot T}\cdot dh</math> | ||
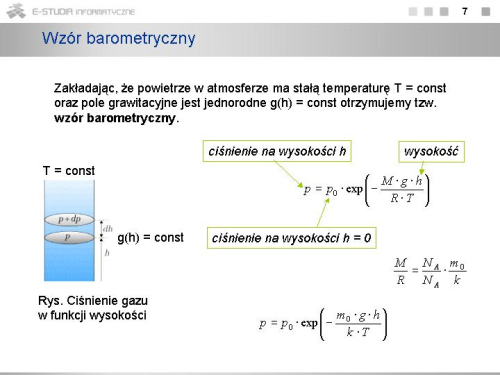
Zakładając, że temperatura atmosfery ma wartość stałą (tzw. atmosfera izotermiczna) i pole grawitacyjne jest jednorodne <math>(g(h) = const)\ | Zakładając, że temperatura atmosfery ma wartość stałą (tzw. atmosfera izotermiczna) i pole grawitacyjne jest jednorodne <math>(g(h) = const)\ </math>, możemy łatwo scałkować to równanie otrzymując | ||
: <math> | : <math>lnp=-\frac{M \cdot g\cdot h}{R\cdot T}+lnC</math> | ||
gdzie <math>lnC\ | gdzie <math>lnC\ </math>, to stała całkowania. | ||
Wynika stąd, że | Wynika stąd, że | ||
: <math> | : <math>p=C\cdot exp\left(-\frac{M \cdot g\cdot h}{R\cdot T}\right)</math> | ||
Dla <math>h=0\ | Dla <math>h=0\ </math>, ciśnienie równe jest ciśnieniu atmosferycznemu <math>p_0\ </math>, na powierzchni Ziemi. Stąd wyznaczamy stałą, <math>C=p_0\ </math>, . Ostatecznie otrzymujemy | ||
: <math> | : <math>p=p_0\cdot exp\left(-\frac{M \cdot g\cdot h}{R\cdot T}\right)</math> | ||
Jest to tzw. '''wzór barometryczny'''. Wynika z niego, że ciśnienie zmienia się z wysokością szybciej dla niższych temperatur oraz dla cięższego gazu, i że zmiana ta ma charakter wykładniczy | Jest to tzw. '''wzór barometryczny'''. Wynika z niego, że ciśnienie zmienia się z wysokością szybciej dla niższych temperatur oraz dla cięższego gazu, i że zmiana ta ma charakter wykładniczy | ||
Wzór barometryczny obowiązuje dla '''atmosfery izotermicznej''', dla której mamy oraz jednorodnego pola grawitacyjnego. Jeżeli warunki te nie są spełnione, należy odpowiednio podstawić zależność funkcyjną temperatury od wysokości oraz zależność <math>g = g(h)\ | Wzór barometryczny obowiązuje dla '''atmosfery izotermicznej''', dla której mamy oraz jednorodnego pola grawitacyjnego. Jeżeli warunki te nie są spełnione, należy odpowiednio podstawić zależność funkcyjną temperatury od wysokości oraz zależność <math>g = g(h)\ </math>, i rozwiązać otrzymane równanie różniczkowe. | ||
Korzystając z faktu, że <math> | Korzystając z faktu, że <math>\frac{M}{R}=\frac{N_A\cdot m_0}{N_A\cdot k}=\frac{m_0}{k}</math> , gdzie <math>m_0\ </math>, - średnia masa cząsteczki powietrza, możemy wzór barometryczny przedstawić w postaci | ||
: <math> | : <math>p=p_0\cdot exp\left(-\frac{m_0 \cdot g\cdot h}{k\cdot T}\right)</math> | ||
|} | |} | ||
| Linia 114: | Linia 114: | ||
|valign="top"|W rozważaniach dotyczących rozkładu Maxwella ignorowaliśmy całkowicie fakt, że cząsteczki poruszają się w polu sił ciężkości, a więc wyróżniony jest kierunek pionowy. Wzór barometryczny wskazuje, że ciężar cząsteczek ma wpływ na rozkład ciśnienia w funkcji wysokości. Jak uwzględnić ten efekt w opisie rozkładu prędkości cząsteczek? | |valign="top"|W rozważaniach dotyczących rozkładu Maxwella ignorowaliśmy całkowicie fakt, że cząsteczki poruszają się w polu sił ciężkości, a więc wyróżniony jest kierunek pionowy. Wzór barometryczny wskazuje, że ciężar cząsteczek ma wpływ na rozkład ciśnienia w funkcji wysokości. Jak uwzględnić ten efekt w opisie rozkładu prędkości cząsteczek? | ||
Przepiszmy w nieco innej formie wzór barometryczny. Zakładając atmosferę izotermiczną, możemy zamienić ciśnienia <math>p\ | Przepiszmy w nieco innej formie wzór barometryczny. Zakładając atmosferę izotermiczną, możemy zamienić ciśnienia <math>p\ </math>, i <math>p_0\ </math>, występujące we wzorze barometrycznym wielkościami <math>n\ </math>, i <math>n_0\ </math>, , które reprezentują koncentrację cząsteczek, czyli ich liczbę w jednostce objętości na wysokości <math>h\ </math>, oraz na powierzchni Ziemi. Wykorzystując to zapiszemy wzór barometryczny w formie | ||
: <math> | : <math>n=n_0\cdot exp\left(-\frac{m_0 \cdot g\cdot h}{k\cdot T}\right)</math> | ||
Zwróćmy uwagę, że wyrażenie <math>m_0\cdot g\cdot h\ | Zwróćmy uwagę, że wyrażenie <math>m_0\cdot g\cdot h\ </math>, jest po prostu energią potencjalną <math>E_p\ </math>, cząsteczki w polu sił ciężkości (przy założeniu jednorodnego pola grawitacyjnego). Więc również | ||
: <math> | : <math>n=n_0\cdot exp\left(-\frac{E_p}{k\cdot T}\right)</math> | ||
Ten wzór wyraża zależność koncentracji cząsteczek od ich wysokości lub grawitacyjnej energii potencjalnej. Wynikający z niego rozkład koncentracji nosi nazwę '''rozkładu Boltzmanna''' i odnosi się nie tylko do pola sił przyciągania ziemskiego, ale do dowolnego pola potencjalnego, jeśli tylko cząsteczki poruszają się chaotycznym ruchem cieplnym. | Ten wzór wyraża zależność koncentracji cząsteczek od ich wysokości lub grawitacyjnej energii potencjalnej. Wynikający z niego rozkład koncentracji nosi nazwę '''rozkładu Boltzmanna''' i odnosi się nie tylko do pola sił przyciągania ziemskiego, ale do dowolnego pola potencjalnego, jeśli tylko cząsteczki poruszają się chaotycznym ruchem cieplnym. | ||
| Linia 132: | Linia 132: | ||
|valign="top"|Stan układu określany przez parametry makroskopowe, jak temperatura, ciśnienie, energia wewnętrzna, itd. nazywamy '''''makrostanem'''''. Stan układu wyznaczony przez określenie stanów wszystkich cząsteczek wchodzących w jego skład nazywamy '''''mikrostanem'''''. Liczba możliwych mikrostanów odpowiadających danemu makrostanowi jest na ogół ogromna, analiza nasza będzie mieć charakter statystyczny. Liczba mikrostanów odpowiadających danemu makrostanowi nazywa się '''''prawdopodobieństwem termodynamicznym''''' lub '''''wagą statystyczną''''' makrostanu. | |valign="top"|Stan układu określany przez parametry makroskopowe, jak temperatura, ciśnienie, energia wewnętrzna, itd. nazywamy '''''makrostanem'''''. Stan układu wyznaczony przez określenie stanów wszystkich cząsteczek wchodzących w jego skład nazywamy '''''mikrostanem'''''. Liczba możliwych mikrostanów odpowiadających danemu makrostanowi jest na ogół ogromna, analiza nasza będzie mieć charakter statystyczny. Liczba mikrostanów odpowiadających danemu makrostanowi nazywa się '''''prawdopodobieństwem termodynamicznym''''' lub '''''wagą statystyczną''''' makrostanu. | ||
Rozpatrzmy sens wagi statystycznej na przykładzie naczynia z gazem, w którym znajduje się <math>N\ | Rozpatrzmy sens wagi statystycznej na przykładzie naczynia z gazem, w którym znajduje się <math>N\ </math>, cząsteczek. Stan danej cząsteczki opiszemy tylko jedną informacją - w której części naczynia, lewej czy prawej, cząsteczka się znajduje. Zbiór tych informacji dla wszystkich <math>N\ </math>, cząsteczek określa '''mikrostan''' naszego układu. (Dla uproszczenia rozważań nie będziemy brać pod uwagę prędkości, kierunku ruchu, masy cząsteczek itp.). | ||
'''Makrostan''' układu określamy podając sumaryczną liczbę cząsteczek z jednej (np. lewej) strony naczynia. Nie bierzemy tu pod uwagę prędkości cząsteczek, ale makroskopowy parametr jakim jest ciśnienie gazu zależne od jego gęstości, a gęstość proporcjonalna jest do liczby cząsteczek w jednostce objętości. Liczba makrostanów, to liczba przypadków, w których <math>k\ | '''Makrostan''' układu określamy podając sumaryczną liczbę cząsteczek z jednej (np. lewej) strony naczynia. Nie bierzemy tu pod uwagę prędkości cząsteczek, ale makroskopowy parametr jakim jest ciśnienie gazu zależne od jego gęstości, a gęstość proporcjonalna jest do liczby cząsteczek w jednostce objętości. Liczba makrostanów, to liczba przypadków, w których <math>k\ </math>, cząsteczek (nie ważne których) znajduje się z lewej strony oraz <math>N-k\ </math>, , z prawej strony. | ||
Liczba mikrostanów dla danego makrostanu, w którym <math>k\ | Liczba mikrostanów dla danego makrostanu, w którym <math>k\ </math>, cząsteczek znajduje się z lewej strony równa jest liczbie kombinacji <math>k\ </math>, - elementowych w zbiorze o <math>N\ </math>, elementach i wynosi <math>W\ </math>,. | ||
|} | |} | ||
| Linia 148: | Linia 148: | ||
Wszystkie możliwe '''mikrostany''' odpowiadające danemu makrostanowi wymienione są w kolejnej kolumnie. Podane są tam wszystkie sposoby, na jakie może być realizowany dany makrostan. W następnej kolumnie znajdują się liczby mikrostanów odpowiadających danemu makrostanowi, czyli wagi statystyczne poszczególnych makrostanów. W kolumnie z prawej strony podane są prawdopodobieństwa realizacji poszczególnych makrostanów. Na dole tablicy podana jest sumaryczna liczba mikrostanów oraz sumaryczne prawdopodobieństwo, które równe jest, oczywiście, jedności. Zakładamy, że cząsteczki są rozróżnialne (tzn. możemy je np. ponumerować). | Wszystkie możliwe '''mikrostany''' odpowiadające danemu makrostanowi wymienione są w kolejnej kolumnie. Podane są tam wszystkie sposoby, na jakie może być realizowany dany makrostan. W następnej kolumnie znajdują się liczby mikrostanów odpowiadających danemu makrostanowi, czyli wagi statystyczne poszczególnych makrostanów. W kolumnie z prawej strony podane są prawdopodobieństwa realizacji poszczególnych makrostanów. Na dole tablicy podana jest sumaryczna liczba mikrostanów oraz sumaryczne prawdopodobieństwo, które równe jest, oczywiście, jedności. Zakładamy, że cząsteczki są rozróżnialne (tzn. możemy je np. ponumerować). | ||
Liczba mikrostanów dla danego makrostanu, w którym <math>k\ | Liczba mikrostanów dla danego makrostanu, w którym <math>k\ </math>, cząsteczek znajduje się z lewej strony równa jest liczbie kombinacji <math>k\ </math>, - elementowych w zbiorze o <math>N\ </math>, elementach i wynosi | ||
: <math> | : <math>W(N, k)=\frac{N!}{k!(N-k)!}</math> | ||
Jest to właśnie waga statystyczna danego makrostanu. Sumaryczna liczba wszystkich mikrostanów wynosi <math>2^N\ | Jest to właśnie waga statystyczna danego makrostanu. Sumaryczna liczba wszystkich mikrostanów wynosi <math>2^N\ </math>,. Prawdopodobieństwo danego makrostanu jest równe stosunkowi jego wagi statystycznej do sumarycznej liczby wszystkich mikrostanów i dla naszego przypadku podane jest w prawej kolumnie tabeli. Prawdopodobieństwo, że dana cząsteczka znajdzie się z prawej lub z lewej strony naczynia jest takie samo, czyli '''prawdopodobieństwa wszystkich mikrostanów są sobie równe'''. Uogólnienie tego stwierdzenia na zdefiniowane w dowolny sposób mikrostany nosi nazwę '''hipotezy ergodycznej'''. | ||
|} | |} | ||
| Linia 182: | Linia 182: | ||
: <math>S=k\cdot lnW</math> | : <math>S=k\cdot lnW</math> | ||
gdzie <math>k\ | gdzie <math>k\ </math>, jest znaną nam już stałą Boltzmanna. Entropia rośnie wraz ze wzrostem prawdopodobieństwa stanu układu, jest logarytmiczną miarą tego prawdopodobieństwa. | ||
|} | |} | ||
| Linia 192: | Linia 192: | ||
|valign="top"|Wymieńmy podstawowe własności entropii wynikające z naszych wcześniejszych rozważań. | |valign="top"|Wymieńmy podstawowe własności entropii wynikające z naszych wcześniejszych rozważań. | ||
1. ''Przemiany nieodwracalne zachodzące w układzie izolowanym prowadzą do wzrostu entropii układu''. Prawo to wyraża wzór <math>dS>0\ | 1. ''Przemiany nieodwracalne zachodzące w układzie izolowanym prowadzą do wzrostu entropii układu''. Prawo to wyraża wzór <math>dS>0\ </math>, . | ||
Przykładem może być rozważany przez nas układ podzielony umownie na część lewą i prawą. Wzrost prawdopodobieństwa statystycznego równoważny jest ze wzrostem entropii tego układu. | Przykładem może być rozważany przez nas układ podzielony umownie na część lewą i prawą. Wzrost prawdopodobieństwa statystycznego równoważny jest ze wzrostem entropii tego układu. | ||
| Linia 209: | Linia 209: | ||
'''Zadanie 10.3''' | '''Zadanie 10.3''' | ||
Oblicz zmianę entropii <math>n_M\ | Oblicz zmianę entropii <math>n_M\ </math>, moli gazu doskonałego w procesie izotermicznego rozprężania od objętości <math>V_0\ </math>, do objętości <math>V_k\ </math>, | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | ||
Układem jest porcja <math>n_M\ | Układem jest porcja <math>n_M\ </math>, moli gazu zawierająca liczbę <math>N\ </math>, identycznych, niezależnych cząsteczek (podukładów). Prawdopodobieństwo stanu <math>W\ </math>, równe jest iloczynowi prawdopodobieństw stanów podukładów <math>w_i(1,2,\ldots,N)\ </math>,. | ||
Dla pojedynczej cząsteczki prawdopodobieństwo jej przebycia w objętości <math>V\ | Dla pojedynczej cząsteczki prawdopodobieństwo jej przebycia w objętości <math>V\ </math>, jest proporcjonalne do <math>V\ </math>,, a dla <math>N\ </math>, cząsteczek do <math>V^{n}\ </math>,. Więc <math>w_i=A\cdot V</math> | ||
:<math> | :<math>W=w_{i}^{N}=(A\cdot V)^N</math> A jest stałą proporcjonalności. Z definicji entropii, będzie: | ||
:<math> | :<math>S=k\cdot N(lnA+lnV)</math> | ||
Liczba cząsteczek i ich temperatura nie zmienia się. Zwiększa się objętość porcji gazu od <math>V_0\ | Liczba cząsteczek i ich temperatura nie zmienia się. Zwiększa się objętość porcji gazu od <math>V_0\ </math>, do <math>V_k\ </math>, i zwiększa się entropia (nieuporządkowanie) układu | ||
<math> | <math>\Delta S=S_k-S_0= k\cdot N(lnA+lnV_k)- k\cdot N(lnA+lnV_0)= k\cdot N\cdot ln\frac{V_k}{V_0}=n_M\cdot R\cdot ln\frac{V_k}{V_0}</math> | ||
</div></div> | </div></div> | ||
| Linia 237: | Linia 237: | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Odpowiedź </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Odpowiedź </span><div class="mw-collapsible-content" style="display:none"> | ||
Przy temperaturze <math>429\, K\ | Przy temperaturze <math>429\, K\ </math>,. | ||
</div></div> | </div></div> | ||
| Linia 245: | Linia 245: | ||
'''Zadanie 10.5''' | '''Zadanie 10.5''' | ||
Izolowany układ dwóch zbiorników. Zbiornik o objętości <math>V_1\ | Izolowany układ dwóch zbiorników. Zbiornik o objętości <math>V_1\ </math>, zawierał <math>n_{M1}\ </math>, moli gazu o temperaturze <math>T\ </math>, . Zbiornik o objętości <math>V_2\ </math>, zawierał <math>n_{M2}\ </math>, moli również o temperaturze <math>T\ </math>, , Oblicz zmianę entropii tych gazów po połączeniu zbiorników i powstaniu mieszaniny. | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Odpowiedź </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Odpowiedź </span><div class="mw-collapsible-content" style="display:none"> | ||
<math> | <math>\Delta S=R\cdot \left(n_{M1}\cdot ln\frac{V_1+V_2}{V_1}+ n_{M2}\cdot ln\frac{V_1+V_2}{V_1} \right)</math> , entropia układu wzrośnie, bo jest to proces nieodwracalny, entropia układu wzrośnie, bo wzrośnie nieuporządkowanie elementów układu. | ||
</div></div> | </div></div> | ||
Aktualna wersja na dzień 21:57, 15 wrz 2023
Wykład
Materiały do ćwiczeń
Zadanie 10.3
Oblicz zmianę entropii , moli gazu doskonałego w procesie izotermicznego rozprężania od objętości , do objętości ,
Rozwiązanie
Zadanie 10.4
Przy jakiej temperaturze średnia prędkość kwadratowa cząsteczek dwutlenku węgla będzie równa średniej prędkości kwadratowej cząsteczek azotu w temperaturze ?
Odpowiedź
Zadanie 10.5
Izolowany układ dwóch zbiorników. Zbiornik o objętości , zawierał , moli gazu o temperaturze , . Zbiornik o objętości , zawierał , moli również o temperaturze , , Oblicz zmianę entropii tych gazów po połączeniu zbiorników i powstaniu mieszaniny.
Odpowiedź
Słowniczek
| wzór barometryczny | podaje zależność ciśnienia atmosferycznego od wysokości nad powierzchnią Ziemi |
| rozkład Maxwella prędkości cząsteczek | rozkład wartości prędkości chaotycznego ruchu cząsteczek gazu doskonałego dla zadanej temperatury i masy cząsteczek |
| rozkład Boltzmanna | rozkład koncentracji cząsteczek w funkcji ich wysokości lub energii potencjalnej. Odnosi się nie tylko do pola sił przyciągania ziemskiego, ale do dowolnego pola potencjalnego, jeśli tylko cząsteczki poruszają się chaotycznym ruchem cieplnym. |
| mikrostan | stan układu w którym opisane są stany wszystkich jego elementów |
| hipoteza ergodyczna | Prawdopodobieństwa wszystkich mikrostanów są jednakowe |
| makrostan | stan układu opisany za pomocą wielkości odnoszących się do całości układu |
| prawdopodobieństwo termodynamiczne (waga statystyczna) | odnosi się do makrostanu układu: liczba mikroskoopowych sposobów realizacji danego makrostanu (liczba mikrostanów odpowiadająca danemu makrostanowi) |
| entropia | definicja statystyczna: wielkość proporcjonalna do logarytmu prawdopodobieństwa termodynamicznego stanu układu |
| fluktuacje | losowe odchylenia danej wielkości od wartości średniej |
| prawo wzrostu entropii | entropia układu izolowanego nie może maleć, w procesach nieodwracalnych entropia układu rośnie |