Matematyka dyskretna 1/Ćwiczenia 5: Współczynniki dwumianowe: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
m Zastępowanie tekstu – „,↵</math>” na „</math>,” |
|||
| (Nie pokazano 3 pośrednich wersji utworzonych przez tego samego użytkownika) | |||
| Linia 2: | Linia 2: | ||
{{cwiczenie|1|cw 1| | {{cwiczenie|1|cw 1| | ||
Wskaż największy wyraz w <math> | Wskaż największy wyraz w <math>n</math>-tym wierszu Trójkąta Pascala i odpowiedź uzasadnij. | ||
}} | }} | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | ||
Największym wyrazem w <math> | Największym wyrazem w <math>n</math>-tym wierszu jest wyraz środkowy | ||
<math> | <math>{n \choose {\left\lfloor n/2 \right\rfloor}}={n \choose {\left\lceil n/2 \right\rceil}}</math>. | ||
Korzystając ze wzoru na postać zwartą współczynnika dwumianowego, | Korzystając ze wzoru na postać zwartą współczynnika dwumianowego, | ||
pokaż <math> | pokaż <math>{n\choose k}<{n\choose k+1}</math> dla <math>k<\left\lfloor n/2 \right\rfloor</math>. | ||
</div></div> | </div></div> | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | ||
Ponieważ <math> | Ponieważ <math>{n\choose k}={n\choose n-k}</math>, dla <math>n\geqslant k\geqslant0</math>, | ||
to aby pokazać, że największym wyrazem w <math> | to aby pokazać, że największym wyrazem w <math>n</math>-tym wierszu jest | ||
<math> | <math>{n\choose{\left\lfloor n/2 \right\rfloor}}={n\choose{\left\lceil n/2 \right\rceil}}</math>, | ||
wystarczy pokazać, że | wystarczy pokazać, że | ||
<center><math> | <center><math>{n\choose k}<{n\choose k+1}</math>,</center> | ||
</math></center> | |||
dla <math> | dla <math>k<\left\lfloor \frac{n}{2} \right\rfloor</math>. | ||
Nierówność ta jest równoważna kolejno | Nierówność ta jest równoważna kolejno | ||
<center><math> | <center><math>\begin{align} \frac{n!}{k!(n-k)!}&<\frac{n!}{(k+1)!(n-k-1)!},\\ | ||
\frac{1}{n-k}&<\frac{1}{k+1},\\ | \frac{1}{n-k}&<\frac{1}{k+1},\\ | ||
k+1&<n-k,\\ | k+1&<n-k,\\ | ||
| Linia 35: | Linia 34: | ||
Ostatnia nierówność zachodzi dla <math> | Ostatnia nierówność zachodzi dla <math>k<\left\lfloor \frac{n}{2} \right\rfloor</math>, | ||
zatem wszystkie poprzednie też zachodzą. | zatem wszystkie poprzednie też zachodzą. | ||
| Linia 44: | Linia 43: | ||
<center><math> | <center><math>{n\choose0}{n\choose k}+{n\choose1}{n-1\choose k-1}+\ldots+{n\choose k}{n-k\choose0} | ||
=2^k{n\choose k} | =2^k{n\choose k}</math></center> | ||
</math></center> | |||
| Linia 52: | Linia 50: | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | ||
Rozważ liczbę kolorowań <math> | Rozważ liczbę kolorowań <math>k</math> rozróżnialnych obiektów wybranych spośród <math>n</math>, | ||
przy użyciu dwu kolorów. | przy użyciu dwu kolorów. | ||
</div></div> | </div></div> | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | ||
Policzmy kolorowania <math> | Policzmy kolorowania <math>k</math> rozróżnialnych obiektów wybranych spośród <math>n</math>, | ||
przy użyciu dwu kolorów (biały i czarny). | przy użyciu dwu kolorów (biały i czarny). | ||
Podzbiór <math> | Podzbiór <math>k</math>-elementowy <math>n</math>-elementowego zbioru obiektów można wybrać | ||
na <math> | na <math>{n\choose k}</math> sposobów i każdy taki podzbiór możemy pokolorować na <math>2^k</math> sposobów. | ||
Zatem liczba interesujących nas kolorowań to <math> | Zatem liczba interesujących nas kolorowań to <math>2^k{n\choose k}</math>. | ||
Policzmy nasze kolorowania inną metodą. | Policzmy nasze kolorowania inną metodą. | ||
Zauważmy, iż dowolne kolorowanie posiada <math> | Zauważmy, iż dowolne kolorowanie posiada <math>i</math> obiektów białych | ||
i <math> | i <math>k-i</math> czarnych dla pewnego <math>i\in\left\lbrace 0,\ldots,k \right\rbrace</math>. | ||
Zatem każde kolorowanie możemy jednoznacznie otrzymać wybierając najpierw <math> | Zatem każde kolorowanie możemy jednoznacznie otrzymać wybierając najpierw <math>i</math> | ||
obiektów spośród wszystkich <math> | obiektów spośród wszystkich <math>n</math> (i kolorując je na biało), | ||
a później z pozostałych <math> | a później z pozostałych <math>n-i</math> obiektów wybierając <math>k-i</math> (kolorując je na czarno). | ||
Możemy to zrobić na <math> | Możemy to zrobić na <math>{n\choose i}{n-i\choose k-i}</math> sposobów, | ||
czyli sumując po wszystkich możliwych wartościach <math> | czyli sumując po wszystkich możliwych wartościach <math>i</math> | ||
otrzymujemy <math> | otrzymujemy <math>\sum_{i=0}^k{n\choose i}{n-i\choose k-i}</math>. | ||
</div></div> | </div></div> | ||
| Linia 78: | Linia 76: | ||
<center><math> | <center><math>{n\choose 0}^2+{n\choose1}^2+\ldots+{n\choose n}^2={2n\choose n}</math></center> | ||
</math></center> | |||
| Linia 85: | Linia 82: | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | ||
Rozważ liczbę wyborów <math> | Rozważ liczbę wyborów <math>n</math> osób z <math>2n</math>-osobowej grupy złożonej z <math>n</math> mężczyzn i <math>n</math> kobiet. | ||
</div></div> | </div></div> | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | ||
Rozważmy na ile sposobów możemy wybrać <math> | Rozważmy na ile sposobów możemy wybrać <math>n</math> osób z grupy <math>n</math> mężczyzn i <math>n</math> kobiet. | ||
Oczywiście, z jednej strony, sposobów wyboru <math> | Oczywiście, z jednej strony, sposobów wyboru <math>n</math> spośród <math>2n</math> osób jest <math>{2n\choose n}</math>. | ||
Alternatywnie zauważmy, że wybierając <math> | Alternatywnie zauważmy, że wybierając <math>n</math> osób wybieramy <math>i</math> mężczyzn i <math>n-i</math> kobiet | ||
dla pewnego <math> | dla pewnego <math>i\in\left\lbrace 0,\ldots,n \right\rbrace</math>. | ||
Dla ustalonego <math> | Dla ustalonego <math>i</math> możemy to wykonać na <math>{n\choose i}{n\choose n-i}={n\choose i}^2</math> | ||
sposobów, zatem sumarycznie liczba możliwości to | sposobów, zatem sumarycznie liczba możliwości to | ||
<math> | <math>\sum_{i=0}^n{n\choose i}^2</math>, co było do pokazania. | ||
</div></div> | </div></div> | ||
| Linia 103: | Linia 100: | ||
<center><math> | <center><math>{n\choose 1}+2{n\choose 2}+\ldots+n{n\choose n}=n2^{n-1}</math></center> | ||
</math></center> | |||
| Linia 110: | Linia 106: | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | ||
Rozważ liczbę wyborów z grupy <math> | Rozważ liczbę wyborów z grupy <math>n</math> osób podzbioru z wyznaczonym w nim przywódcą. | ||
</div></div> | </div></div> | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | ||
Rozważmy na ile sposobów można wybrać z grupy <math> | Rozważmy na ile sposobów można wybrać z grupy <math>n</math> osób podzbiór z wyznaczonym w nim przywódcą. Z jednej strony możemy najpierw wybrać przywódcę spośród <math>n</math> osób, a później dobrać do niego dowolny podzbiór zbioru pozostałych <math>n-1</math> osób. Możemy to zrobić na <math>n2^{n-1}</math> sposobów. | ||
Z drugiej strony możemy najpierw wybrać niepusty podzbiór <math> | Z drugiej strony możemy najpierw wybrać niepusty podzbiór <math>i</math>-elementowy (dla <math>i\in\left\lbrace 1,\ldots,n \right\rbrace</math>) zbioru <math>n</math> osób, a potem wybrać spośród nich przywódcę na jeden z <math>i</math> sposobów. Sumując po wszystkich <math>i</math> możemy wykonać to na <math>\sum_{i=0}^ni{n\choose i}</math> sposobów, co było do pokazania. | ||
</div></div> | </div></div> | ||
| Linia 124: | Linia 120: | ||
<center><math> | <center><math>1^2{n\choose 1}^2+2^2{n\choose 2}^2+\ldots+n^2{n\choose n}^n=n^2{2n-2\choose n-1}</math></center> | ||
</math></center> | |||
| Linia 131: | Linia 126: | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | ||
Rozważ liczbę wyborów z grupy <math> | Rozważ liczbę wyborów z grupy <math>2n</math> osobowej złożonej z <math>n</math> mężczyzn i <math>n</math> kobiet | ||
podzbioru, w którym liczba kobiet i mężczyzn jest równa | podzbioru, w którym liczba kobiet i mężczyzn jest równa | ||
i ponadto, w którym wyróżnionych jest dwóch przywódców jeden mężczyzna i jedna kobieta. | i ponadto, w którym wyróżnionych jest dwóch przywódców jeden mężczyzna i jedna kobieta. | ||
| Linia 138: | Linia 133: | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | ||
Dla rozgrzewki rozważmy, na ile sposobów z grupy <math> | Dla rozgrzewki rozważmy, na ile sposobów z grupy <math>2n</math> osób | ||
złożonej z <math> | złożonej z <math>n</math> mężczyzn i <math>n</math> kobiet | ||
można wybrać podzbiór osób, w którym liczba mężczyzn i kobiet jest równa. | można wybrać podzbiór osób, w którym liczba mężczyzn i kobiet jest równa. | ||
Nietrudno zauważyć, iż jest to <math> | Nietrudno zauważyć, iż jest to <math>\sum_{i=0}^n{n\choose i}^2</math>, | ||
a z [[#cw_3|Ćwiczenia 3]] | a z [[#cw_3|Ćwiczenia 3]] | ||
wiemy, że <math> | wiemy, że <math>\sum_{i=0}^n{n\choose i}^2={2n\choose n}</math>. | ||
Zastanówmy się teraz z kolei na ile sposobów można wybrać | Zastanówmy się teraz z kolei na ile sposobów można wybrać | ||
z tej samej <math> | z tej samej <math>2n</math> osobowej grupy podzbiór, | ||
w którym liczba mężczyzn i kobiet jest równa | w którym liczba mężczyzn i kobiet jest równa | ||
i dodatkowo wśród wybranych jest wyróżnionych dwóch przywódców: | i dodatkowo wśród wybranych jest wyróżnionych dwóch przywódców: | ||
jeden mężczyzna i jedna kobieta. | jeden mężczyzna i jedna kobieta. | ||
Dla ustalonego <math> | Dla ustalonego <math>i\in\left\lbrace 1,\ldots,n \right\rbrace</math> możemy najpierw wybrać <math>i</math> kobiet i <math>i</math> mężczyzn | ||
na <math> | na <math>{n\choose i}^2</math> sposobów, | ||
a potem spośród nich wyłonić przywódców na <math> | a potem spośród nich wyłonić przywódców na <math>i^2</math> sposobów. | ||
Zatem sumarycznie możemy dokonać wyboru na <math> | Zatem sumarycznie możemy dokonać wyboru na <math>\sum_{i=1}^ni^2{n\choose i}^2</math>. | ||
Alternatywnie możemy najpierw wybrać przywódcę jednego spośród <math> | Alternatywnie możemy najpierw wybrać przywódcę jednego spośród <math>n</math> mężczyzn | ||
i jednej spośród <math> | i jednej spośród <math>n</math> kobiet na <math>n^2</math> sposobów, | ||
a potem uzupełnić wybrańców dobierając im <math> | a potem uzupełnić wybrańców dobierając im <math>i</math> mężczyzn i tyle samo kobiet, | ||
dla <math> | dla <math>i\in\left\lbrace 0,\ldots,n-1 \right\rbrace</math>. | ||
Z początkowej naszej refleksji możemy to zrobić na <math> | Z początkowej naszej refleksji możemy to zrobić na <math>{2n-2\choose n-1}</math> sposobów. | ||
Podsumowując, interesującego nas wyboru możemy dokonać na <math> | Podsumowując, interesującego nas wyboru możemy dokonać na <math>n^2{2n-2\choose n-1}</math>, | ||
co było do pokazania. | co było do pokazania. | ||
</div></div> | </div></div> | ||
[[File:SW 8.CW1.svg|250x250px|thumb|right|SW 8.CW1.swf]] | |||
{{cwiczenie|6|cw 6| | {{cwiczenie|6|cw 6| | ||
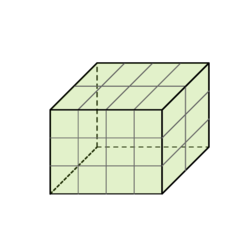
Ile prostokątów zawiera się w kratce <math> | Ile prostokątów zawiera się w kratce <math>n\times n</math>? | ||
Dla przykładu w kratce <math> | Dla przykładu w kratce <math>2\times2</math> jest ich <math>9</math>. | ||
}} | }} | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | ||
Rozważ ile prostokątów w kratce <math> | Rozważ ile prostokątów w kratce <math>n\times n</math> zawiera się w górnej lewej podkratce | ||
<math> | <math>m\times m</math> (dla <math>m<n</math>), | ||
ale nie zawiera się w górnej lewej podkratce <math> | ale nie zawiera się w górnej lewej podkratce <math>(m-1)\times(m-1)</math>. | ||
</div></div> | </div></div> | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | ||
[[File:SW 8.CW2.svg|250x250px|thumb|left|SW 8.CW2.swf]] | |||
[[File:SW 8.CW3.svg|250x250px|thumb|right|SW 8.CW3.swf]] | |||
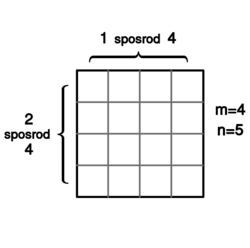
Policzmy ile prostokątów w kratce <math> | Policzmy ile prostokątów w kratce <math>n\times n</math> położonych jest w lewej górnej podkratce | ||
<math> | <math>m\times m</math> i przylega do chociaż jednej z wewnętrznych (czyli dolnej bądź prawej) | ||
krawędzi podkratki. | krawędzi podkratki. | ||
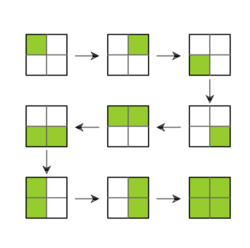
Kilka przykładów takich prostokątów przedstawiamy poniżej dla <math> | Kilka przykładów takich prostokątów przedstawiamy poniżej dla <math>n=5</math> i <math>m=4</math>: | ||
Prostokąt przylegający do prawej pionowej krawędzi podkratki <math> | Prostokąt przylegający do prawej pionowej krawędzi podkratki <math>m\times m</math> i nieprzylegający do dolnej poziomej krawędzi jest jednoznacznie wyznaczony przez wybór <math>1</math> pionowej krawędzi spośród <math>m</math> i dwu poziomych krawędzi spośród <math>m</math>. | ||
Zatem jest dokładnie <math> | Zatem jest dokładnie <math>{m\choose 1}{m\choose 2}=\frac{m^2(m-1)}{2}</math> takich prostokątów. Analogicznie jest <math>\frac{m^2(m-1)}{2}</math> prostokątów przylegających do dolnej krawędzi podkratki <math>m\times m</math> i nieprzylegających do prawej. W końcu jest dokładnie <math>m^2</math> prostokątów leżących w prawym dolnym narożniku podkratki <math>m\times m</math>, gdyż są one jednoznacznie wyznaczone przez wybór <math>1</math> poziomej linii spośród <math>m</math> i <math>1</math> pionowej linii spośród <math>m</math>. | ||
Zatem w sumie jest | Zatem w sumie jest | ||
| Linia 207: | Linia 193: | ||
<center> | <center> | ||
<math> | <math>\frac{m^2(m-1)}{2}+\frac{m^2(m-1)}{2}+m^2=m^3</math>, | ||
</math> | |||
</center> | </center> | ||
prostokątów w podkratce <math> | prostokątów w podkratce <math>m\times m</math> przylegających do chociaż jednej wewnętrznej krawędzi. Sumując po <math>m\in\left\lbrace 1,\ldots,n \right\rbrace</math> otrzymujemy liczbę wszystkich prostokątów w kratce <math>n\times n</math>, czyli jest ich | ||
<center> | <center> | ||
<math> | <math>1^3+2^3+\ldots+n^3 = \left( \frac{n(n+1)}{2} \right)^2</math> | ||
</math> | |||
</center> | </center> | ||
| Linia 228: | Linia 212: | ||
<center> | <center> | ||
<math> | <math>(-4)^n{-\frac{1}{2}\choose n}={2n\choose n}</math> | ||
</math> | |||
</center> | </center> | ||
| Linia 240: | Linia 223: | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | ||
Dowód przez indukcję względem <math> | Dowód przez indukcję względem <math>n</math>. | ||
Dla <math> | Dla <math>n=1</math> mamy | ||
<center> | <center> | ||
<math> | <math>(-4)^1{-\frac{1}{2}\choose 1}=(-4)\frac{-\frac{1}{2}}{1}=2={2\choose 1}</math> | ||
</math> | |||
</center> | </center> | ||
| Linia 254: | Linia 236: | ||
<center> | <center> | ||
<math> | <math>\begin{align} {2(n+1)\choose n+1} | ||
&=\frac{(2n+1)(2n+2)}{(n+1)^2}{2n\choose n}\\ | &=\frac{(2n+1)(2n+2)}{(n+1)^2}{2n\choose n}\\ | ||
&=\frac{2(2n+1)}{n+1}(-4)^n{-\frac{1}{2}\choose n}\\ | &=\frac{2(2n+1)}{n+1}(-4)^n{-\frac{1}{2}\choose n}\\ | ||
| Linia 270: | Linia 252: | ||
<center> | <center> | ||
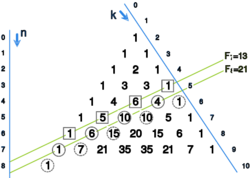
<math> | <math>f_{n+1}=\sum_{k=0}^{n}{n-k\choose k} | ||
</math> | </math> | ||
</center> | </center> | ||
gdzie <math> | gdzie <math>f_n</math> jest <math>n</math>-tą liczbą Fibonacci'ego | ||
}} | }} | ||
| Linia 285: | Linia 267: | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | ||
[[File:SW 8.CW4.svg|250x250px|thumb|right|SW 8.CW4.swf]] | |||
Dowód indukcyjny względem <math> | Dowód indukcyjny względem <math>n</math>. Dla <math>n=0</math> i <math>n=1</math> mamy odpowiednio | ||
<math> | <math>f_1=1= {0\choose0}=1</math> i <math>f_2=1=1+0={1\choose0}+{0\choose1}</math>. | ||
Ponadto: | Ponadto: | ||
<center> | <center> | ||
<math> | <math>\begin{align} f_{n+2}&=f_n+f_{n+1}\\ | ||
&=\sum_{k=0}^{n-1}{n-1-k\choose k}+\sum_{k=0}^n{n-k\choose k}\\ | &=\sum_{k=0}^{n-1}{n-1-k\choose k}+\sum_{k=0}^n{n-k\choose k}\\ | ||
&={n\choose 0}+\sum_{k=0}^{n-1}\left({n-1-k\choose k}+{n-(k+1)\choose k+1}\right)\\ | &={n\choose 0}+\sum_{k=0}^{n-1}\left({n-1-k\choose k}+{n-(k+1)\choose k+1}\right)\\ | ||
Aktualna wersja na dzień 21:50, 11 wrz 2023
Współczynniki dwumianowe
Ćwiczenie 1
Wskaż największy wyraz w -tym wierszu Trójkąta Pascala i odpowiedź uzasadnij.
Wskazówka
Rozwiązanie
Ćwiczenie 2
Posługując się interpretacją kombinatoryczną pokaż, że
Wskazówka
Rozwiązanie
Ćwiczenie 3
Posługując się interpretacją kombinatoryczną pokaż, że
Wskazówka
Rozwiązanie
Ćwiczenie 4
Posługując się interpretacją kombinatoryczną pokaż, że
Wskazówka
Rozwiązanie
Ćwiczenie 5
Posługując się interpretacją kombinatoryczną pokaż, że
Wskazówka
Rozwiązanie
Ćwiczenie 6
Ile prostokątów zawiera się w kratce ? Dla przykładu w kratce jest ich .
Wskazówka
Rozwiązanie
Ćwiczenie 7
Udowodnij, że:
Wskazówka
Rozwiązanie
Ćwiczenie 8
Udowodnij, że:
gdzie jest -tą liczbą Fibonacci'ego
Wskazówka
Rozwiązanie